Comment refaçonner un graphe networkx en Python?
J'ai donc créé une façon vraiment naïve (probablement inefficace) de générer des diagrammes de hasse.
Question:
j'ai 4 dimensions... pqrs .
je veux l'afficher uniformément (tesseract) mais je ne sais pas comment le remodeler. comment refaçonner un graphe networkx en Python?
j'ai j'ai vu quelques exemples de personnes utilisant spring_layout() et draw_circular() mais il ne forme pas de la façon que je cherche parce qu'ils ne sont pas uniformes.
Est-il possible de remodeler mon graphique et de la rendre uniforme? (c'est-à-dire refaçonner mon diagramme de hasse en forme de tesseract (de préférence en utilisant nx.draw() )
voici à quoi ressemble actuellement la mine:
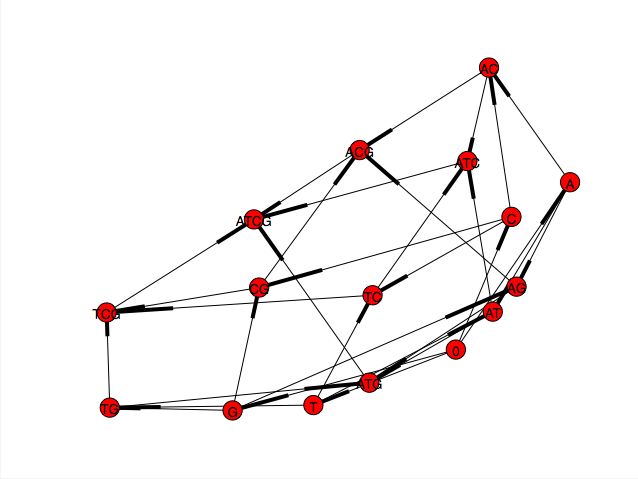
Voici mon code pour générer le diagramme hasse de n dimensions
#!/usr/bin/python
import networkx as nx
import matplotlib.pyplot as plt
import itertools
H = nx.DiGraph()
axis_labels = ['p','q','r','s']
D_len_node = {}
#Iterate through axis labels
for i in xrange(0,len(axis_labels)+1):
#Create edge from empty set
if i == 0:
for ax in axis_labels:
H.add_edge('O',ax)
else:
#Create all non-overlapping combinations
combinations = [c for c in itertools.combinations(axis_labels,i)]
D_len_node[i] = combinations
#Create edge from len(i-1) to len(i) #eg. pq >>> pqr, pq >>> pqs
if i > 1:
for node in D_len_node[i]:
for p_node in D_len_node[i-1]:
#if set.intersection(set(p_node),set(node)): Oops
if all(p in node for p in p_node) == True: #should be this!
H.add_edge(''.join(p_node),''.join(node))
#Show Plot
nx.draw(H,with_labels = True,node_shape = 'o')
plt.show()
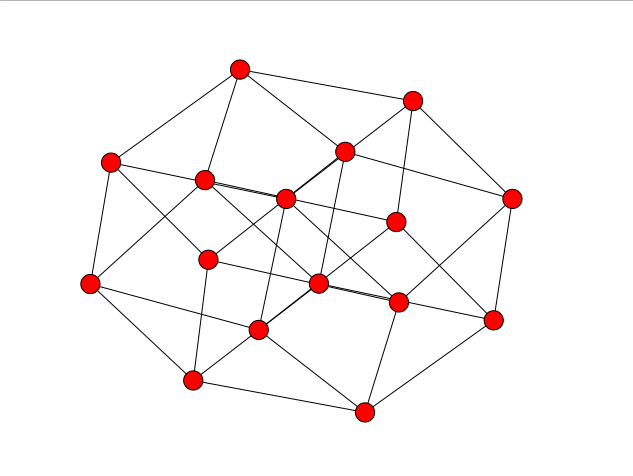
je veux remodeler comme ceci:
si quelqu'un connaît une façon plus facile de faire des diagrammes de Hasse, s'il vous plaît partagez un peu de sagesse!--14--> mais ce n'est pas l'objectif principal de ce post.
1 réponses
il s'agit d'une réponse pragmatique, plutôt que purement mathématique.
je pense que vous avez deux problèmes avec la mise en page, l'autre avec votre réseau.
1. Réseau
Vous avez trop d'arêtes dans votre réseau pour représenter l'unité de tesseract. Avertissement Je ne suis pas un expert en maths ici - est venu à cela de l'angle de pointage (étiquette matplotlib). Veuillez expliquer si je me trompe.
votre désirée projection et, par exemple, le wolfram mathworld page pour un diagramme de Hasse pour n=4 a seulement 4 bords connectés tous les noeuds, alors que vous avez 6 bords aux 2 et 7 bords aux 3 noeuds bit. Votre graphique connecte complètement chaque" niveau", c.-à-d. vecteurs 4-D avec 0 1 les valeurs se connectent à tous les vecteurs avec 1 1 valeur, qui se connectent alors à tous les vecteurs avec 2 1 valeurs et ainsi de suite. Ceci est le plus évident dans la projection basée sur la réponse Wikipédia (2ème image ci-dessous)
2. Projection
Je n'ai pas pu trouver un algorithme ou une bibliothèque pré-écrite pour projeter automatiquement le tesseract 4D sur un plan 2D, mais j'ai trouvé quelques exemples, ex: Wikipedia. À partir de cela, vous pouvez élaborer un ensemble de coordination qui vous conviendrait et passer que dans le nx.draw() appel.
voici un exemple-j'ai inclus deux ensembles de coordonnées, un qui ressemble à la projection que vous montrez ci-dessus, un qui correspond celui - ci de wikipedia.
import networkx as nx
import matplotlib.pyplot as plt
import itertools
H = nx.DiGraph()
axis_labels = ['p','q','r','s']
D_len_node = {}
#Iterate through axis labels
for i in xrange(0,len(axis_labels)+1):
#Create edge from empty set
if i == 0:
for ax in axis_labels:
H.add_edge('O',ax)
else:
#Create all non-overlapping combinations
combinations = [c for c in itertools.combinations(axis_labels,i)]
D_len_node[i] = combinations
#Create edge from len(i-1) to len(i) #eg. pq >>> pqr, pq >>> pqs
if i > 1:
for node in D_len_node[i]:
for p_node in D_len_node[i-1]:
if set.intersection(set(p_node),set(node)):
H.add_edge(''.join(p_node),''.join(node))
#This is manual two options to project tesseract onto 2D plane
# - many projections are available!!
wikipedia_projection_coords = [(0.5,0),(0.85,0.25),(0.625,0.25),(0.375,0.25),
(0.15,0.25),(1,0.5),(0.8,0.5),(0.6,0.5),
(0.4,0.5),(0.2,0.5),(0,0.5),(0.85,0.75),
(0.625,0.75),(0.375,0.75),(0.15,0.75),(0.5,1)]
#Build the "two cubes" type example projection co-ordinates
half_coords = [(0,0.15),(0,0.6),(0.3,0.15),(0.15,0),
(0.55,0.6),(0.3,0.6),(0.15,0.4),(0.55,1)]
#make the coords symmetric
example_projection_coords = half_coords + [(1-x,1-y) for (x,y) in half_coords][::-1]
print example_projection_coords
def powerset(s):
ch = itertools.chain.from_iterable(itertools.combinations(s, r) for r in range(len(s)+1))
return [''.join(t) for t in ch]
pos={}
for i,label in enumerate(powerset(axis_labels)):
if label == '':
label = 'O'
pos[label]= example_projection_coords[i]
#Show Plot
nx.draw(H,pos,with_labels = True,node_shape = 'o')
plt.show()
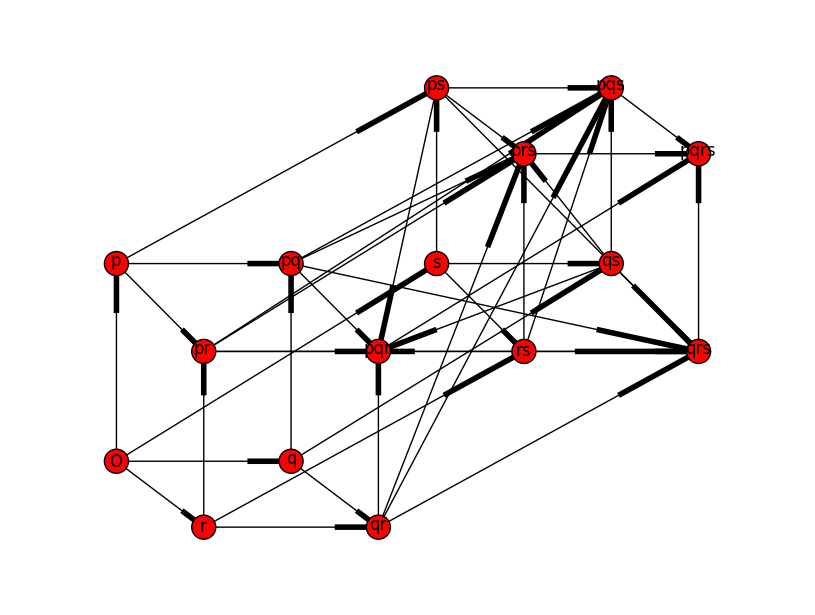
Note-à moins que vous ne changiez ce que j'ai mentionné dans 1. ci-dessus, ils ont toujours votre structure de bord, donc ne sera pas exactement la même que les exemples du web. Voici à quoi il ressemble avec votre code de génération de réseau existant - vous pouvez voir les bords supplémentaires si vous le comparez à votre exemple (par exemple Je ne fais pas cela pr doit être connecté à pqs:
'deux cubes' projection
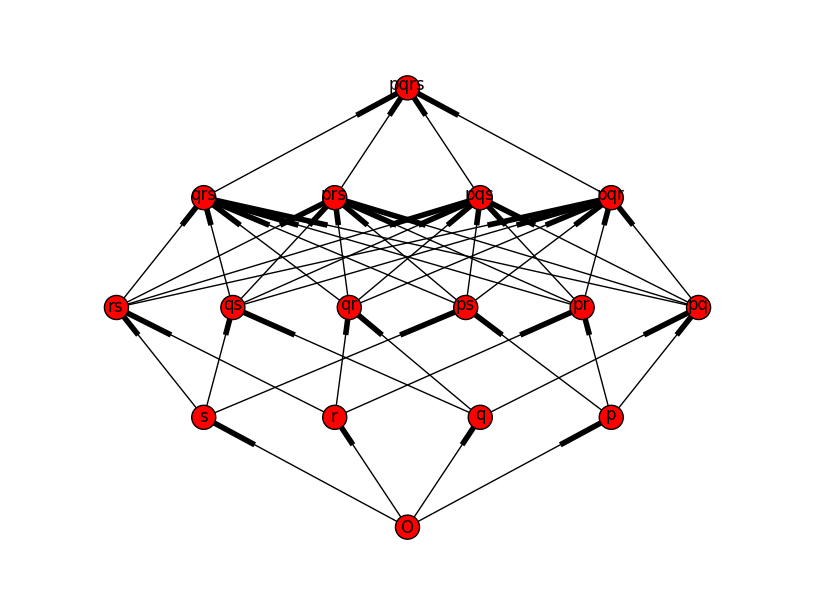
Wikimedia exemple de projection
Remarque:
si vous voulez entrer dans les mathématiques de faire vos propres projections (et de construire pos mathématiquement), vous pourriez regarder cette note de recherche.
EDIT:
la curiosité a pris le dessus sur moi et j'ai dû chercher une voie mathématique pour ce faire. J'ai trouvé ce blog - dont le résultat principal est la matrice de projection:
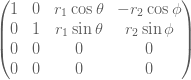
cela m'a amené à développer cette fonction pour projeter chaque étiquette, en prenant l'étiquette contenant " p "pour signifier que le point a la valeur 1 sur l'axe "p", c'est-à-dire que nous avons affaire à l'unité tesseract. Donc:
def construct_projection(label):
r1 = r2 = 0.5
theta = math.pi / 6
phi = math.pi / 3
x = int( 'p' in label) + r1 * math.cos(theta) * int('r' in label) - r2 * math.cos(phi) * int('s' in label)
y = int( 'q' in label) + r1 * math.sin(theta) * int('r' in label) + r2 * math.sin(phi) * int('s' in label)
return (x,y)
donne une belle projection dans un octogone 2D régulier avec tous les points distincts.
exécuter en le programme ci-dessus, il suffit de remplacer
pos[label] = example_projection_coords[i]
pos[label] = construct_projection(label)
Ce qui donne le résultat:
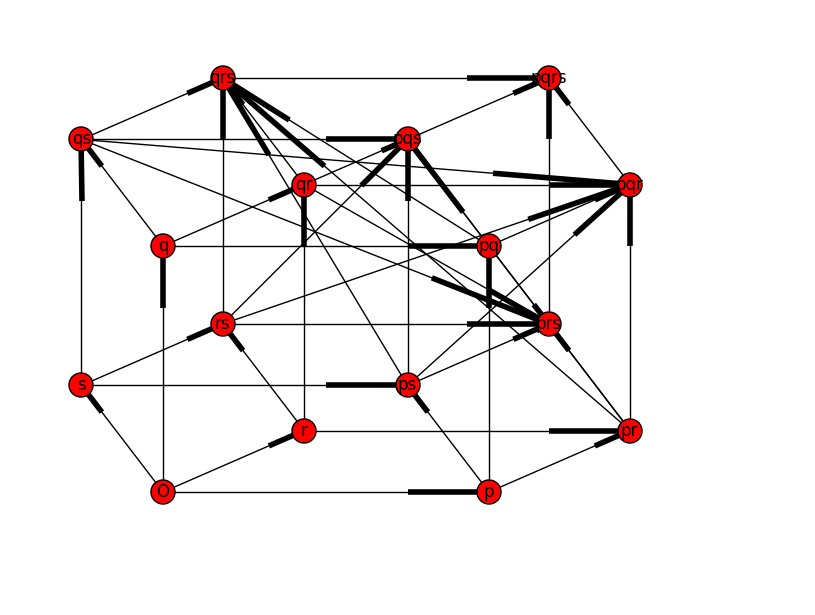
jouer r1,r2,theta et phi au contenu de votre coeur :)