Comment normaliser un histogramme dans MATLAB?
Comment normaliser un histogramme tels que l'aire sous la fonction de densité de probabilité est égale à 1?
7 réponses
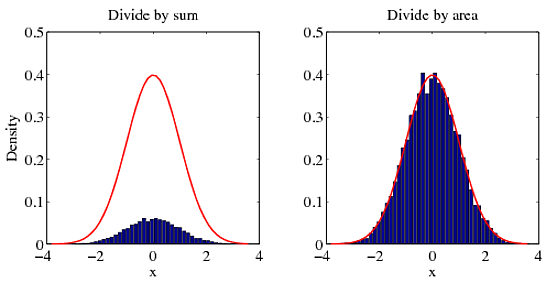
ma réponse à cela est la même que dans une réponse à votre question précédente . Pour une fonction de densité de probabilité, l'intégrale sur l'espace entier est 1 . En divisant par la somme et non , on obtient la densité correcte. Pour obtenir la bonne densité, vous devez diviser par la surface. Pour illustrer mon point de vue, essayez l'exemple suivant.
[f, x] = hist(randn(10000, 1), 50); % Create histogram from a normal distribution.
g = 1 / sqrt(2 * pi) * exp(-0.5 * x .^ 2); % pdf of the normal distribution
% METHOD 1: DIVIDE BY SUM
figure(1)
bar(x, f / sum(f)); hold on
plot(x, g, 'r'); hold off
% METHOD 2: DIVIDE BY AREA
figure(2)
bar(x, f / trapz(x, f)); hold on
plot(x, g, 'r'); hold off
vous pouvez voir par vous-même quelle méthode est d'accord avec la bonne réponse (courbe rouge).
une autre méthode (plus simple que la méthode 2) pour normaliser l'histogramme est de diviser par sum(f * dx) qui exprime l'intégrale de la fonction de densité de probabilité, i.e.
% METHOD 3: DIVIDE BY AREA USING sum()
figure(3)
dx = diff(x(1:2))
bar(x, f / sum(f * dx)); hold on
plot(x, g, 'r'); hold off
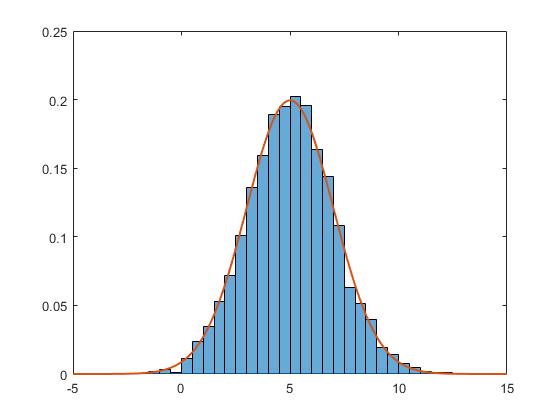
depuis 2014b, Matlab dispose de ces routines de normalisation intégrées nativement dans la fonction histogram (voir le fichier d'aide pour les 6 routines offertes par cette fonction). Voici un exemple utilisant le PDF normalisation (la somme de tous les bacs est 1).
data = 2*randn(5000,1) + 5; % generate normal random (m=5, std=2)
h = histogram(data,'Normalization','pdf') % PDF normalization
le PDF correspondant est
Nbins = h.NumBins;
edges = h.BinEdges;
x = zeros(1,Nbins);
for counter=1:Nbins
midPointShift = abs(edges(counter)-edges(counter+1))/2;
x(counter) = edges(counter)+midPointShift;
end
mu = mean(data);
sigma = std(data);
f = exp(-(x-mu).^2./(2*sigma^2))./(sigma*sqrt(2*pi));
les deux ensemble donne
hold on;
plot(x,f,'LineWidth',1.5)
une amélioration qui pourrait très bien être due au succès de la question actuelle et de la réponse acceptée!
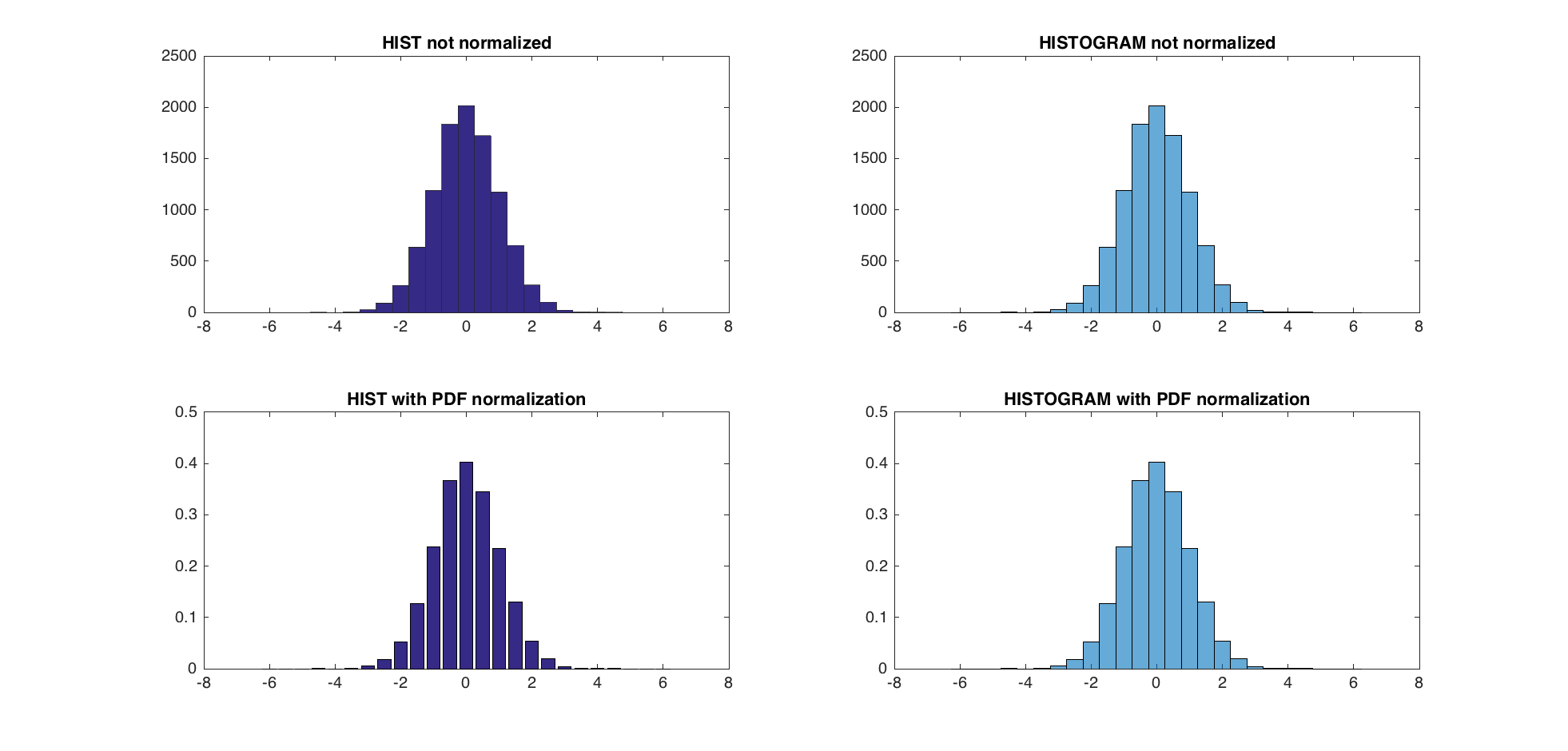
modifier - l'utilisation de hist et histc est non recommandé maintenant, et histogram devrait être utilisé à la place. Attention, aucune des 6 façons de créer des bacs avec cette nouvelle fonction produira les boîtes hist et histc . Il y a un script Matlab pour mettre à jour l'ancien code pour s'adapter à la façon dont histogram est appelé (bin edges au lieu de bin centers - link ). Ce faisant, on peut comparer les pdf méthodes de normalisation DE @abcd ( trapz et sum ) et Matlab ( pdf ).
3 pdf méthode de normalisation donner des résultats presque identiques (dans la gamme de eps ) .
TEST:
A = randn(10000,1);
centers = -6:0.5:6;
d = diff(centers)/2;
edges = [centers(1)-d(1), centers(1:end-1)+d, centers(end)+d(end)];
edges(2:end) = edges(2:end)+eps(edges(2:end));
figure;
subplot(2,2,1);
hist(A,centers);
title('HIST not normalized');
subplot(2,2,2);
h = histogram(A,edges);
title('HISTOGRAM not normalized');
subplot(2,2,3)
[counts, centers] = hist(A,centers); %get the count with hist
bar(centers,counts/trapz(centers,counts))
title('HIST with PDF normalization');
subplot(2,2,4)
h = histogram(A,edges,'Normalization','pdf')
title('HISTOGRAM with PDF normalization');
dx = diff(centers(1:2))
normalization_difference_trapz = abs(counts/trapz(centers,counts) - h.Values);
normalization_difference_sum = abs(counts/sum(counts*dx) - h.Values);
max(normalization_difference_trapz)
max(normalization_difference_sum)
la différence maximale entre la nouvelle normalisation PDF et la première est de 5.5511 e-17.
hist peut non seulement tracer un histogramme, mais aussi vous rendre le nombre d'éléments dans chaque bin, de sorte que vous pouvez obtenir ce nombre, le normaliser en divisant chaque bin par le total et de tracer le résultat en utilisant bar . Exemple:
Y = rand(10,1);
C = hist(Y);
C = C ./ sum(C);
bar(C)
ou si vous voulez une doublure:
bar(hist(Y) ./ sum(hist(Y)))
de la Documentation:
Edit: Cette solution répond à la question Comment faire pour avoir la somme de toutes les cellules égal à 1 . Cette approximation n'est valable que si la taille de votre bin est petite par rapport à la variance de vos données. La somme utilisée ici correspond à une simple formule de quadrature, les plus complexes peuvent être utilisés comme trapz comme proposé par R. M.
[f,x]=hist(data)
la surface de chaque barre est Hauteur*Largeur. Puisque MATLAB choisira des points équidistants pour les barres, la largeur est donc:
delta_x = x(2) - x(1)
maintenant, si nous additionnons toutes les barres individuelles, la superficie totale s'élèvera à
A=sum(f)*delta_x
ainsi le tracé à l'échelle correcte est obtenu par
bar(x, f/sum(f)/(x(2)-x(1)))
la zone de PDF d'abcd n'est pas une, ce qui est impossible comme souligné dans de nombreux commentaires. Hypothèses faites dans de nombreuses réponses ici
- suppose une distance constante entre les bords consécutifs.
- la probabilité sous
pdfdevrait être 1. La normalisation doit être faite commeNormalizationavecprobability, et non commeNormalizationavecpdf, dans histogram() et hist().
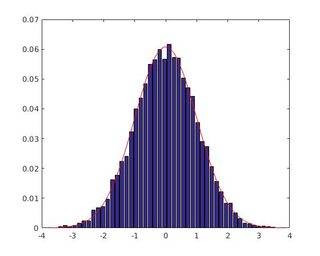
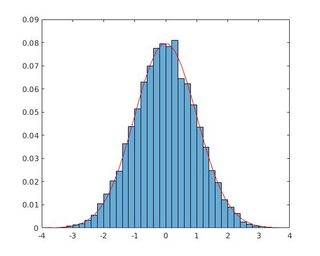
Fig. 1 résultat de l'approche hist (), Fig. 2 Sortie de l'approche histogram () 1519220920"
l'amplitude maximale diffère entre deux approches qui proposent qu'il y ait une erreur dans l'approche de hist () parce que l'approche de histogram () utilise la normalisation standard.
Je suppose que l'erreur avec l'approche de hist () ici est au sujet de la normalisation comme partiellement pdf , pas complètement comme probability .
Code avec hist() [obsolète]
Quelques remarques
- premier contrôle:
sum(f)/Ndonne1siNbinsréglé manuellement. - pdf exige la largeur de la cellule (
dx) dans le graphiqueg
Code
%http://stackoverflow.com/a/5321546/54964
N=10000;
Nbins=50;
[f,x]=hist(randn(N,1),Nbins); % create histogram from ND
%METHOD 4: Count Densities, not Sums!
figure(3)
dx=diff(x(1:2)); % width of bin
g=1/sqrt(2*pi)*exp(-0.5*x.^2) .* dx; % pdf of ND with dx
% 1.0000
bar(x, f/sum(f));hold on
plot(x,g,'r');hold off
sortie est en Figue. 1.
Code avec histogramme ()
Quelques remarques
- d'Abord vérifier: a)
sum(f)est1siNbinsajusté avec de l'histogramme()'s la Normalisation de la probabilité, b)sum(f)/Nest 1 siNbinsest réglé manuellement sans normalisation. - pdf exige la largeur de la cellule (
dx) dans le graphiqueg
Code
%%METHOD 5: with histogram()
% http://stackoverflow.com/a/38809232/54964
N=10000;
figure(4);
h = histogram(randn(N,1), 'Normalization', 'probability') % hist() deprecated!
Nbins=h.NumBins;
edges=h.BinEdges;
x=zeros(1,Nbins);
f=h.Values;
for counter=1:Nbins
midPointShift=abs(edges(counter)-edges(counter+1))/2; % same constant for all
x(counter)=edges(counter)+midPointShift;
end
dx=diff(x(1:2)); % constast for all
g=1/sqrt(2*pi)*exp(-0.5*x.^2) .* dx; % pdf of ND
% Use if Nbins manually set
%new_area=sum(f)/N % diff of consecutive edges constant
% Use if histogarm() Normalization probability
new_area=sum(f)
% 1.0000
% No bar() needed here with histogram() Normalization probability
hold on;
plot(x,g,'r');hold off
sortie Fig. 2 et les résultats escomptés sont atteints: zone 1.0000.
Matlab: 2016a
Système: Linux Ubuntu 16.04 64 bits
Noyau Linux 4.6
pour certaines Distributions, Cauchy je pense, j'ai constaté que trapz surestimera la zone, et donc le pdf changera en fonction du nombre de bacs que vous sélectionnez. Dans ce cas, je fais
[N,h]=hist(q_f./theta,30000); % there Is a large range but most of the bins will be empty
plot(h,N/(sum(N)*mean(diff(h))),'+r')
il y a un excellent guide en trois parties pour ajustements D'histogrammes dans MATLAB ( rupture de lien original , archive.org link ), la première partie est sur l'Étirement d'Histogramme.