Comment mettre en œuvre la profondeur première recherche de graphe avec aprroach non récursif
eh Bien, j'ai passé beaucoup de temps sur cette question. Cependant, je ne peux trouver des solutions avec des méthodes non-récursives pour un arbre: Non récursive pour l'arbre , ou méthode récursive pour le graphe, récursive pour le graphe .
et beaucoup de tutoriels(Je ne fournis pas ces liens ici) ne fournissent pas les approches aussi bien. Ou le tutoriel est totalement erronée. S'il vous plaît aider moi.
mise à Jour:
il est vraiment difficile de décrire:
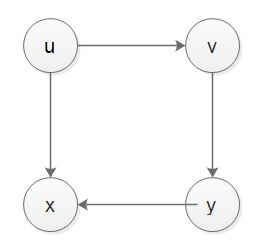
si j'ai un graphique non corrigé:
1
/ |
4 | 2
3 /
1-- 2-- 3 --1 c'est un cycle.
au pas: push the neighbors of the popped vertex into the stack
WHAT'S THE ORDER OF THE VERTEXES SHOULD BE PUSHED?
si l'ordre poussé est 2 4 3, le sommet de la pile est:
| |
|3|
|4|
|2|
_
après avoir fait sauter les noeuds, nous avons eu le résultat: 1 - > 3 -> 4 -> 2 au lieu de 1--> 3 --> 2 -->4.
C'EST INCORRECT. QUELLE CONDITION DOIS-JE AJOUTER POUR ARRÊTER CE SCÉNARIO?
13 réponses
A DFS sans récursion est fondamentalement la même que BFS - mais utiliser une stack au lieu d'une file d'attente que la structure de données.
Le fil Itératif DFS vs Récursive DFS et les différents éléments de commande les poignées avec les deux approches et la différence entre eux (et il y en a! vous ne traverserez pas les noeuds dans le même ordre!)
l'algorithme pour l'approche itérative est essentiellement:
DFS(source):
s <- new stack
visited <- {} // empty set
s.push(source)
while (s is not empty):
current <- s.pop()
if (current is in visited):
continue
visited.add(current)
// do something with current
for each node v such that (current,v) is an edge:
s.push(v)
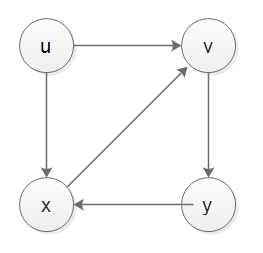
ce n'est pas une réponse, mais un commentaire étendu, montrant l'application de l'algorithme dans la réponse de @amit au graphique dans la version actuelle de la question, en supposant que 1 est le noeud de départ et ses voisins sont poussés dans l'ordre 2, 4, 3:
1
/ | \
4 | 2
3 /
Actions Stack Visited
======= ===== =======
push 1 [1] {}
pop and visit 1 [] {1}
push 2, 4, 3 [2, 4, 3] {1}
pop and visit 3 [2, 4] {1, 3}
push 1, 2 [2, 4, 1, 2] {1, 3}
pop and visit 2 [2, 4, 1] {1, 3, 2}
push 1, 3 [2, 4, 1, 1, 3] {1, 3, 2}
pop 3 (visited) [2, 4, 1, 1] {1, 3, 2}
pop 1 (visited) [2, 4, 1] {1, 3, 2}
pop 1 (visited) [2, 4] {1, 3, 2}
pop and visit 4 [2] {1, 3, 2, 4}
push 1 [2, 1] {1, 3, 2, 4}
pop 1 (visited) [2] {1, 3, 2, 4}
pop 2 (visited) [] {1, 3, 2, 4}
appliquant ainsi l'algorithme poussant les voisins de 1 dans l'ordre 2, 4, 3 résultats dans l'ordre de visite 1, 3, 2, 4. Indépendamment de l'ordre de poussée pour les voisins de 1, 2 et 3 seront adjacents dans l'ordre de visite parce que celui qui est visité le premier poussera l'autre, qui n'est pas encore visité, ainsi que 1 qui a été visité.
la logique DFS devrait être:
1) si le noeud courant n'est pas visité, visitez le noeud et marquez-le comme visité
151940920"
2) pour tous ses voisins qui n'ont pas été visités, les pousser à la pile
par exemple, définissons une classe GraphNode en Java:
class GraphNode {
int index;
ArrayList<GraphNode> neighbors;
}
et voici la DFS sans récursion:
void dfs(GraphNode node) {
// sanity check
if (node == null) {
return;
}
// use a hash set to mark visited nodes
Set<GraphNode> set = new HashSet<GraphNode>();
// use a stack to help depth-first traversal
Stack<GraphNode> stack = new Stack<GraphNode>();
stack.push(node);
while (!stack.isEmpty()) {
GraphNode curr = stack.pop();
// current node has not been visited yet
if (!set.contains(curr)) {
// visit the node
// ...
// mark it as visited
set.add(curr);
}
for (int i = 0; i < curr.neighbors.size(); i++) {
GraphNode neighbor = curr.neighbors.get(i);
// this neighbor has not been visited yet
if (!set.contains(neighbor)) {
stack.push(neighbor);
}
}
}
}
on peut utiliser la même logique faire DFS de manière récursive, clone graphique etc.
la récursion est un moyen d'utiliser la pile d'appels pour stocker l'état de traversée du graphe. Vous pouvez utiliser la pile explicitement, par exemple en ayant une variable locale de type std::stack , alors vous n'aurez pas besoin de la récursion pour implémenter la DFS, mais juste une boucle.
d'accord. si vous êtes toujours à la recherche d'un code java
dfs(Vertex start){
Stack<Vertex> stack = new Stack<>(); // initialize a stack
List<Vertex> visited = new ArrayList<>();//maintains order of visited nodes
stack.push(start); // push the start
while(!stack.isEmpty()){ //check if stack is empty
Vertex popped = stack.pop(); // pop the top of the stack
if(!visited.contains(popped)){ //backtrack if the vertex is already visited
visited.add(popped); //mark it as visited as it is not yet visited
for(Vertex adjacent: popped.getAdjacents()){ //get the adjacents of the vertex as add them to the stack
stack.add(adjacent);
}
}
}
for(Vertex v1 : visited){
System.out.println(v1.getId());
}
}
code Python. La complexité temporelle est O ( V + E ) où V et E sont respectivement le nombre de sommets et d'arêtes. La complexité de l'espace est O ( V ) en raison du pire des cas où il ya un chemin qui contient chaque vertex sans aucun retour en arrière (c.-à-d. le chemin de recherche est un chaîne linéaire ).
la pile stocke les tuples de la forme (vertex, vertex_edge_index) afin que la DFS puisse être reprise à partir d'un vertex particulier au bord immédiatement après le dernier bord qui a été traité à partir de ce vertex (tout comme la pile d'appels de fonction d'un DFS récursif).
le code de l'exemple utilise un digraphe complet où chaque vertex est connecté à chaque autre vertex. Il n'est donc pas nécessaire de stocker une liste de bord explicite pour chaque noeud, car le graphe est une liste de bord (le graphe g contient chaque sommet).
numv = 1000
print('vertices =', numv)
G = [Vertex(i) for i in range(numv)]
def dfs(source):
s = []
visited = set()
s.append((source,None))
time = 1
space = 0
while s:
time += 1
current, index = s.pop()
if index is None:
visited.add(current)
index = 0
# vertex has all edges possible: G is a complete graph
while index < len(G) and G[index] in visited:
index += 1
if index < len(G):
s.append((current,index+1))
s.append((G[index], None))
space = max(space, len(s))
print('time =', time, '\nspace =', space)
dfs(G[0])
sortie:
time = 2000
space = 1000
noter que time ici mesure V opérations et non E . La valeur est numv *2 parce que chaque sommet est considéré deux fois, une fois à la découverte et une fois à la finition.
en fait, stack n'est pas en mesure de gérer le temps de découverte et le temps de finition, si nous voulons implémenter DFS avec stack, et si nous voulons gérer le temps de découverte et le temps de finition, nous aurions besoin de recourir à une autre pile d'enregistreurs, mon implémentation est montrée ci-dessous, avoir un test correct, ci-dessous est pour le cas-1, le cas-2 et le cas-3 graph.
from collections import defaultdict
class Graph(object):
adj_list = defaultdict(list)
def __init__(self, V):
self.V = V
def add_edge(self,u,v):
self.adj_list[u].append(v)
def DFS(self):
visited = []
instack = []
disc = []
fini = []
for t in range(self.V):
visited.append(0)
disc.append(0)
fini.append(0)
instack.append(0)
time = 0
for u_ in range(self.V):
if (visited[u_] != 1):
stack = []
stack_recorder = []
stack.append(u_)
while stack:
u = stack.pop()
visited[u] = 1
time+=1
disc[u] = time
print(u)
stack_recorder.append(u)
flag = 0
for v in self.adj_list[u]:
if (visited[v] != 1):
flag = 1
if instack[v]==0:
stack.append(v)
instack[v]= 1
if flag == 0:
time+=1
temp = stack_recorder.pop()
fini[temp] = time
while stack_recorder:
temp = stack_recorder.pop()
time+=1
fini[temp] = time
print(disc)
print(fini)
if __name__ == '__main__':
V = 6
G = Graph(V)
#==============================================================================
# #for case 1
# G.add_edge(0,1)
# G.add_edge(0,2)
# G.add_edge(1,3)
# G.add_edge(2,1)
# G.add_edge(3,2)
#==============================================================================
#==============================================================================
# #for case 2
# G.add_edge(0,1)
# G.add_edge(0,2)
# G.add_edge(1,3)
# G.add_edge(3,2)
#==============================================================================
#for case 3
G.add_edge(0,3)
G.add_edge(0,1)
G.add_edge(1,4)
G.add_edge(2,4)
G.add_edge(2,5)
G.add_edge(3,1)
G.add_edge(4,3)
G.add_edge(5,5)
G.DFS()
je pense que vous devez utiliser un tableau booléen visited[n] pour vérifier si le noeud courant est visité ou pas plus tôt.
un algorithme récursif fonctionne très bien pour DFS alors que nous essayons de plonger aussi profondément que nous le pouvons, c'est à dire. dès qu'on trouve un vertex Non exploré, on va explorer son premier voisin non exploré tout de suite. Vous devez sortir de la boucle for dès que vous trouvez le premier voisin non exploré.
for each neighbor w of v
if w is not explored
mark w as explored
push w onto the stack
BREAK out of the for loop
je pense que c'est une DFS optimisée en ce qui concerne l'espace-corrigez-moi si je me trompe.
s = stack
s.push(initial node)
add initial node to visited
while s is not empty:
v = s.peek()
if for all E(v,u) there is one unvisited u:
mark u as visited
s.push(u)
else
s.pop
utilisant la pile et implémentant comme fait par la pile d'appel dans le processus de récursion -
l'idée est de pousser un vertex dans la pile, puis de pousser son vertex adjacent qui est stocké dans une liste de contiguïté à l'index du vertex et puis de continuer ce processus jusqu'à ce que nous ne puissions pas aller plus loin dans le graphe, maintenant si nous ne pouvons pas aller de l'avant dans le graphe, alors nous allons supprimer le vertex qui est actuellement sur le dessus de la pile car il est incapable de nous emmener sur un sommet quelconque qui est inconnu.
maintenant, en utilisant stack nous nous occupons du point que le vertex n'est retiré de la pile que lorsque tous les vertices qui peuvent être explorés à partir du vertex courant ont été visités, ce qui était fait par le processus de récursion automatiquement.
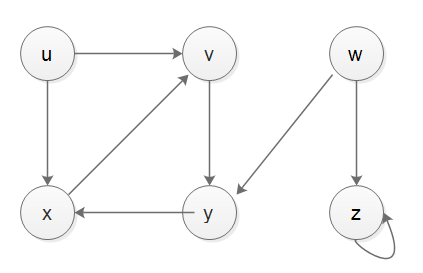
voir l'exemple du graphique ici.
( 0 ( 1 ( 2 ( 4 4 ) 2 ) ( 3 3 ) 1 ) 0 ) ( 6 ( 5 5 ) ( 7 7 ) 6 )
ci-dessus entre parenthèses indiquent l'ordre dans lequel le sommet est ajouté sur la pile et retiré de la pile, de sorte qu'une parenthèse pour un sommet est fermé uniquement lorsque tous les sommets peuvent être visités ont été fait.
(ici j'ai utilisé la représentation de la liste de contiguïté et implémenté comme un vecteur de liste (vecteur > AdjList) en utilisant C++ STL)
void DFSUsingStack() {
/// we keep a check of the vertices visited, the vector is set to false for all vertices initially.
vector<bool> visited(AdjList.size(), false);
stack<int> st;
for(int i=0 ; i<AdjList.size() ; i++){
if(visited[i] == true){
continue;
}
st.push(i);
cout << i << '\n';
visited[i] = true;
while(!st.empty()){
int curr = st.top();
for(list<int> :: iterator it = AdjList[curr].begin() ; it != AdjList[curr].end() ; it++){
if(visited[*it] == false){
st.push(*it);
cout << (*it) << '\n';
visited[*it] = true;
break;
}
}
/// We can move ahead from current only if a new vertex has been added on the top of the stack.
if(st.top() != curr){
continue;
}
st.pop();
}
}
}
le Code Java suivant sera pratique: -
private void DFS(int v,boolean[] visited){
visited[v]=true;
Stack<Integer> S = new Stack<Integer>();
S.push(v);
while(!S.isEmpty()){
int v1=S.pop();
System.out.println(adjLists.get(v1).name);
for(Neighbor nbr=adjLists.get(v1).adjList; nbr != null; nbr=nbr.next){
if (!visited[nbr.VertexNum]){
visited[nbr.VertexNum]=true;
S.push(nbr.VertexNum);
}
}
}
}
public void dfs() {
boolean[] visited = new boolean[adjLists.size()];
for (int v=0; v < visited.length; v++) {
if (!visited[v])/*This condition is for Unconnected Vertices*/ {
System.out.println("\nSTARTING AT " + adjLists.get(v).name);
DFS(v, visited);
}
}
}
beaucoup de gens diront que la DFS non récursive est juste BFS avec une pile plutôt qu'une queue. Ce n'est pas exact, laisse-moi t'expliquer un peu plus.
DFS récursifs
DFS récursif utilise la pile d'appels pour maintenir l'état, ce qui signifie que vous ne gérez pas une pile séparée vous-même.
Cependant, pour un grand graphe, DFS récursive (ou toute fonction récursive qui est) peut entraîner une profonde récursion, qui peut écraser votre problème avec un un débordement de pile (pas ce site, la vraie chose ).
DFS Non récursifs
DFS n'est pas la même que la BFS. Il a une utilisation d'espace différente, mais si vous l'implémentez comme BFS, mais en utilisant une pile plutôt qu'une file, vous utiliserez plus d'espace que DFS non récursive.
pourquoi plus d'espace?
considérez ceci:
// From non-recursive "DFS"
for (auto i&: adjacent) {
if (!visited(i)) {
stack.push(i);
}
}
et comparez - le avec ceci:
// From recursive DFS
for (auto i&: adjacent) {
if (!visited(i)) {
dfs(i);
}
}
dans le premier morceau de code vous mettez tous les noeuds adjacents dans la pile avant itération au prochain sommet adjacent et qui a un coût d'espace. Si le graphique est importante, cela peut faire une différence significative.
Que faire alors?
si vous décidez de résoudre le problème d'espace en itérant au-dessus de la liste adjacente encore une fois après avoir popping la pile, cela va ajouter le coût de complexité de temps.
une solution est d'ajouter des articles à la pile un par un, comme vous le visitez. Pour ce faire, vous pouvez enregistrer un itérateur dans la pile pour reprendre l'itération après popping.
manière Paresseuse
en C/C++, une approche paresseuse est de compiler votre programme avec une plus grande taille de pile et d'augmenter la taille de pile via ulimit , mais c'est vraiment nul. En Java, vous pouvez définir la taille de la pile comme paramètre JVM.