Comment implémenter une file d'attente en utilisant deux piles?
supposons que nous ayons deux piles et aucune autre variable temporaire.
est-il possible de" construire " une structure de données de file d'attente en utilisant seulement les deux piles?
17 réponses
gardez 2 piles, appelons-les inbox et outbox .
enquête :
- Pousser l'élément nouveau sur
inbox
file d'attente :
-
si
outboxest vide, remplissez-le en enlevant chaque élément deinboxet en le poussant suroutbox -
de la Pop et de retour, l'élément supérieur de
outbox
en utilisant cette méthode, chaque élément sera dans chaque pile exactement une fois - ce qui signifie que chaque élément sera poussé deux fois et poussé deux fois, donnant des opérations amorties en temps constant.
Voici une implémentation en Java:
public class Queue<E>
{
private Stack<E> inbox = new Stack<E>();
private Stack<E> outbox = new Stack<E>();
public void queue(E item) {
inbox.push(item);
}
public E dequeue() {
if (outbox.isEmpty()) {
while (!inbox.isEmpty()) {
outbox.push(inbox.pop());
}
}
return outbox.pop();
}
}
A-Comment Inverser Une Pile
pour comprendre comment construire une file d'attente en utilisant deux piles, vous devez comprendre comment inverser une pile cristalline. Rappelez-vous comment stack fonctionne, il est très similaire à la pile de vaisselle sur votre cuisine. Le dernier plat lavé sera sur le dessus de la pile propre, qui est appelé comme L ast I n F irst o ut (LIFO) dans l'ordinateur sciences.
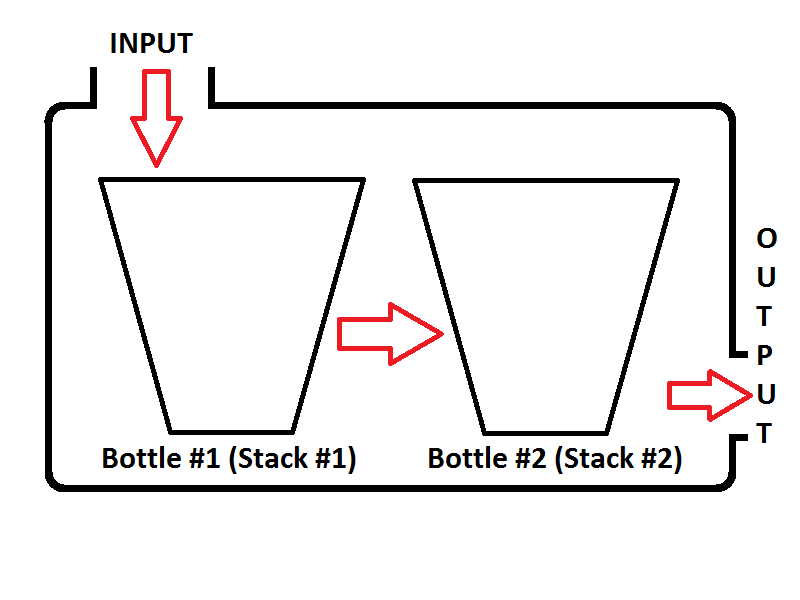
laisse imaginer notre pile comme une bouteille comme ci-dessous;
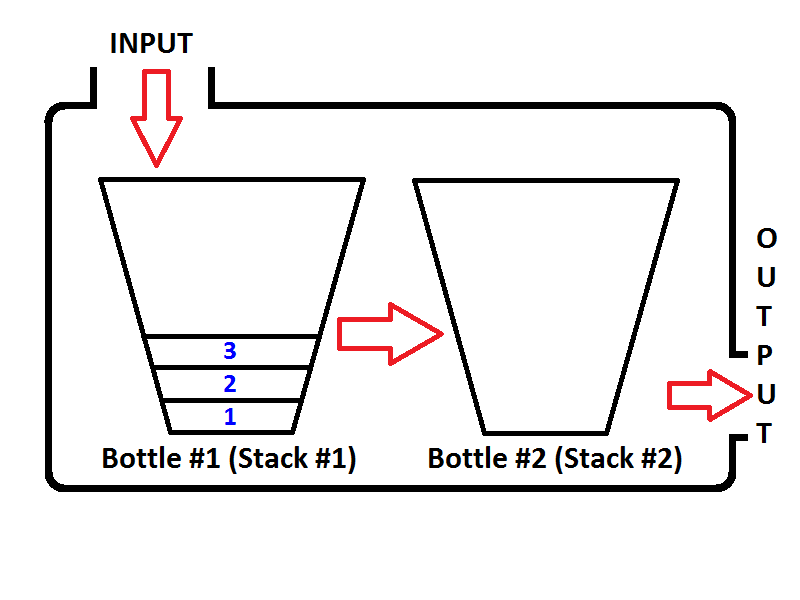
si nous poussons des entiers 1,2,3 respectivement, alors 3 sera sur le dessus de la pile. Parce que 1 sera poussé d'abord, puis 2 sera mis sur le dessus de 1. Enfin, 3 seront placés sur le dessus de la pile et le dernier état de notre pile représenté comme une bouteille sera comme ci-dessous;
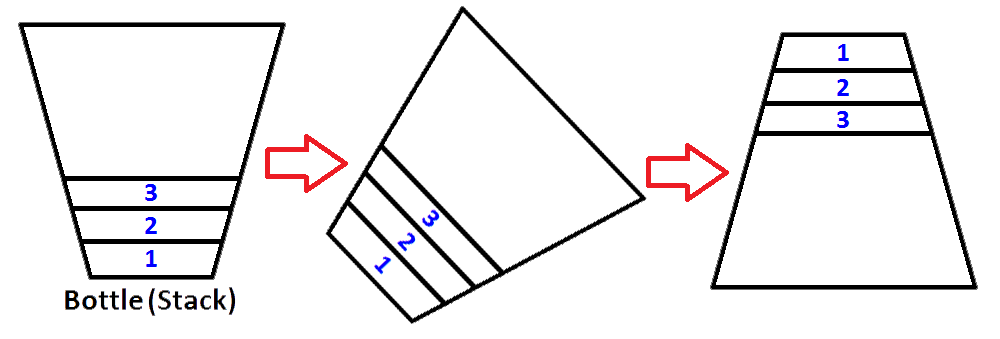
maintenant nous avons notre pile représentée comme une bouteille est peuplée avec des valeurs 3,2,1. Et nous voulons inverser la pile pour que l'élément supérieur de la pile soit 1 et l'élément inférieur de la pile sera 3. Ce que nous pouvons faire ? On peut prendre la bouteille et la tenir à l'envers pour que toutes les valeurs soient inversées dans l'ordre ?
oui on peut faire ça, mais c'est une bouteille. Pour faire la même démarche, nous avons besoin d'avoir une deuxième pile qui va stocker la première pile éléments dans l'ordre inverse. Mettons notre pile peuplée à gauche et notre nouvelle pile vide à droite. Pour inverser l'ordre des éléments, nous allons pop chaque élément de la pile de gauche, et les pousser à la pile de droite. Vous pouvez voir ce qui se passe pendant que nous le faisons sur l'image ci-dessous;
pour savoir comment inverser une pile.
B-Utilisation De Deux Piles Comme File D'Attente
sur la partie précédente, j'ai expliqué comment nous pouvons inverser l'ordre des éléments de pile. C'était important, parce que si on push et pop des éléments de la pile, la sortie sera exactement dans l'ordre inverse d'une file d'attente. En pensant à un exemple, poussons le tableau des entiers {1, 2, 3, 4, 5} à une pile. Si nous pop les éléments et les imprimer jusqu'à ce que la pile soit vide, nous obtiendrons le tableau dans l'ordre inverse de pousser l'ordre, qui sera {5, 4, 3, 2, 1} rappelez-vous que pour la même entrée, si nous définissons la file d'attente jusqu'à ce que la file d'attente soit vide, la sortie sera {1, 2, 3, 4, 5} . Il est donc évident que, pour la même entrée de commande des éléments de sortie de la file d'attente est exactement l'inverse de la sortie d'une pile. Comme nous savons inverser une pile en utilisant une pile supplémentaire, nous pouvons construire une file d'attente en utilisant deux piles.
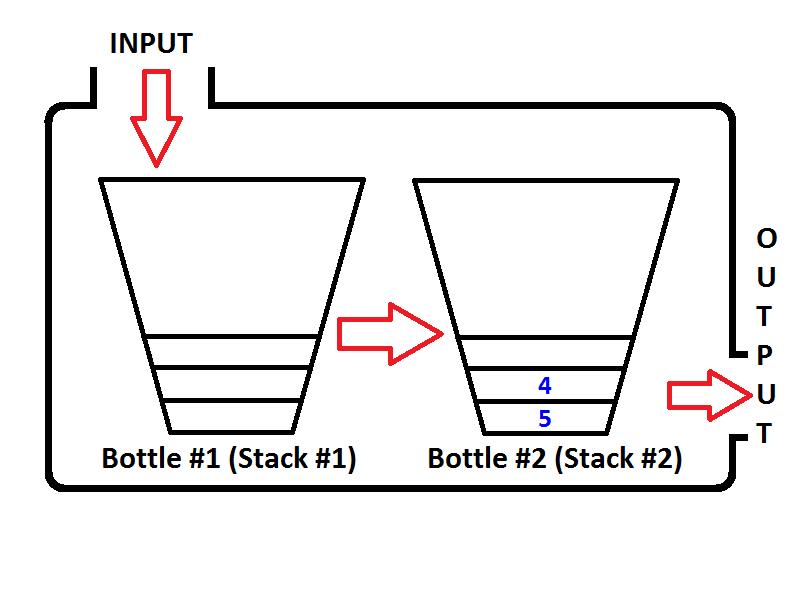
notre modèle de file d'attente se composera de deux piles. Une pile sera utilisée pour l'opération enqueue (pile n ° 1 à gauche, appelée pile D'entrée), une autre pile sera utilisée pour l'opération dequeue (pile n ° 2 à droite, appelée pile de sortie). Regardez l'image ci-dessous;
Notre pseudo-code est comme ci-dessous;
Mettre En File D'Attente De L'Opération
Push every input element to the Input Stack
Résorption De L'Opération
If ( Output Stack is Empty)
pop every element in the Input Stack
and push them to the Output Stack until Input Stack is Empty
pop from Output Stack
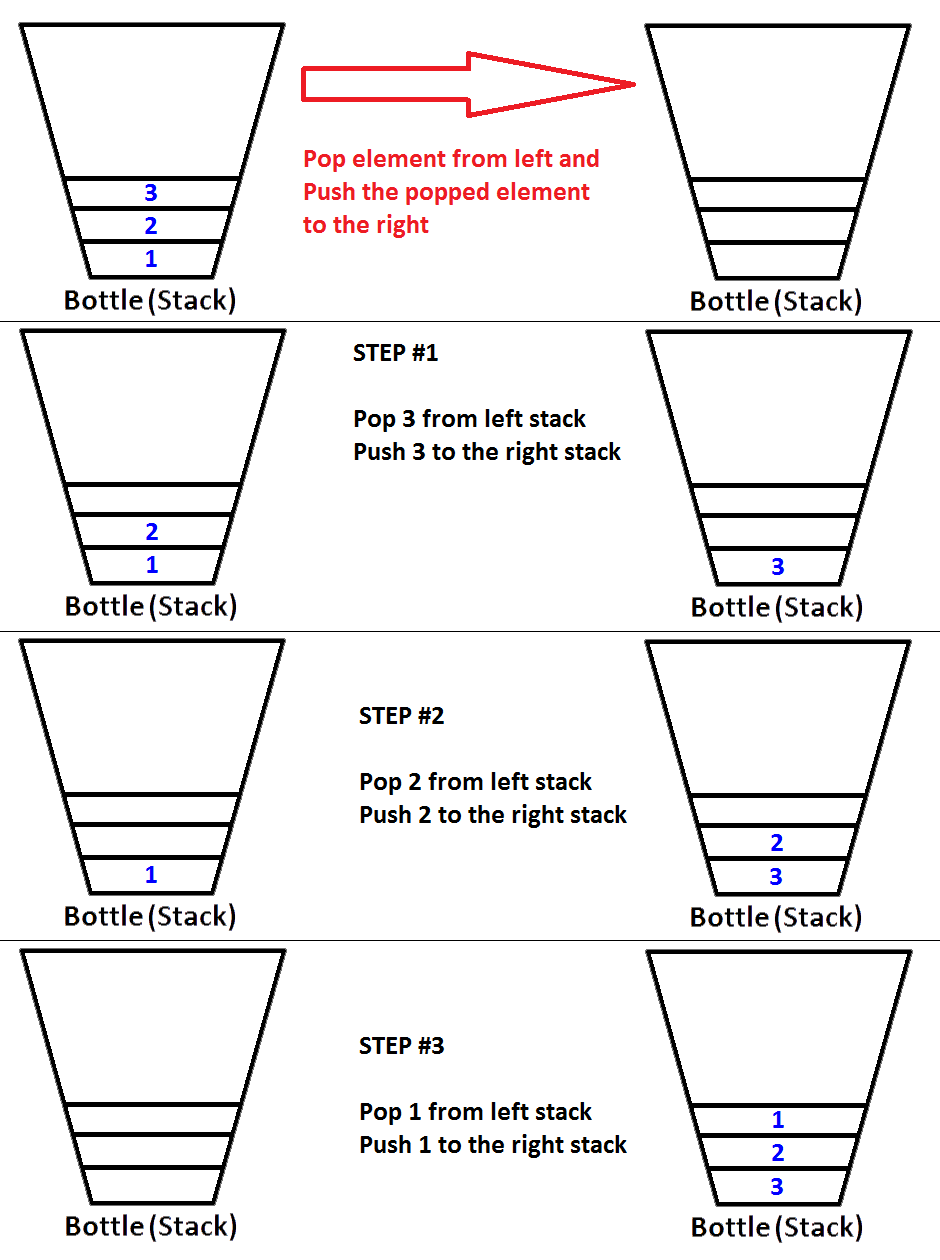
nous allons mettre en file d'attente les entiers {1, 2, 3} , respectivement. Les entiers seront poussés sur la d'Entrée de la Pile ( "1519170920 Pile" #1 ), qui est situé sur la gauche;
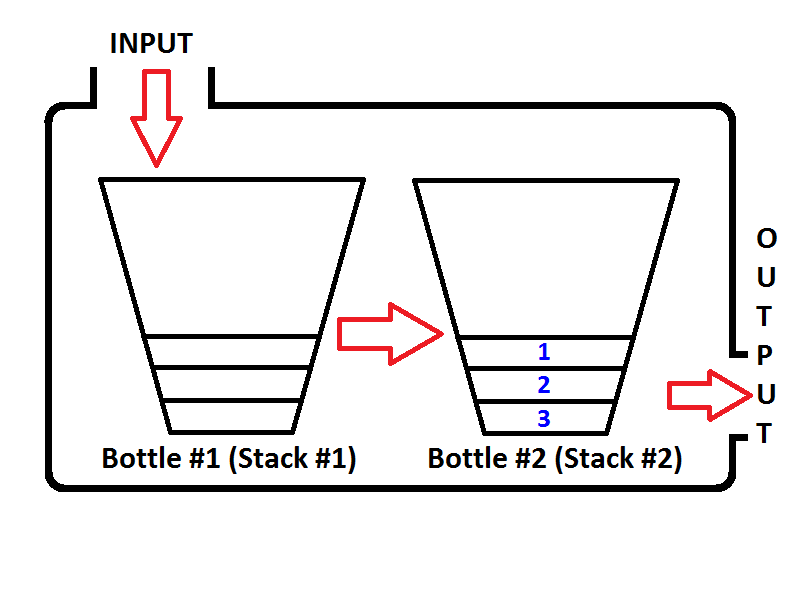
alors que se passera-t-il si nous exécutons une résorption de l'opération? Chaque fois qu'une opération de série est exécutée, file va vérifier si la pile de sortie est vide ou non(voir le pseudo-code ci-dessus) si la pile de sortie est vide, alors la pile D'entrée va être extraite sur la sortie de sorte que les éléments de la pile D'entrée seront inversés. Avant de retourner une valeur, l'état de la file d'attente sera comme ci-dessous;
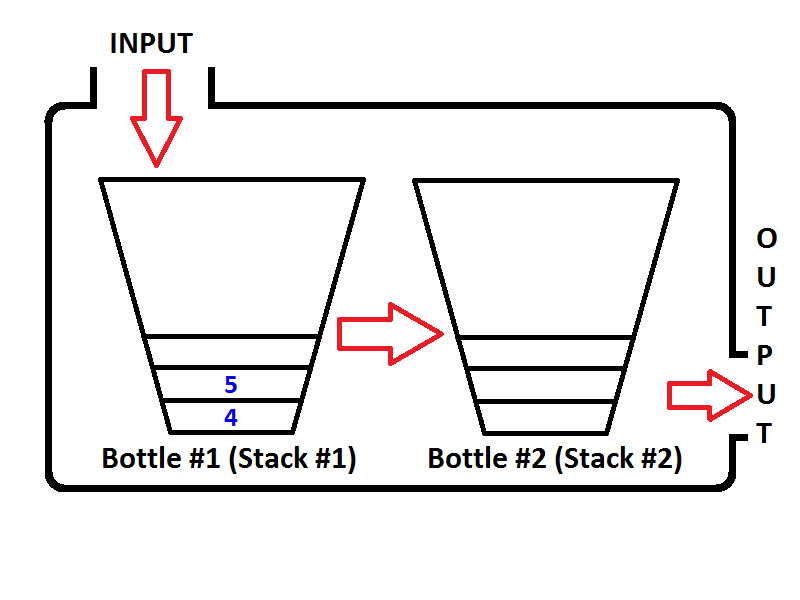
Vérifier le ordre des éléments dans la pile de sortie (Stack #2). Il est évident que nous pouvons pop les éléments de la pile de sortie de sorte que la sortie sera la même que si nous sommes dans une file d'attente. Ainsi, si nous exécutons deux opérations dequeue, nous obtiendrons d'abord {1, 2} respectivement. Alors l'élément 3 sera le seul élément de la pile de sortie, et la pile D'entrée sera vide. Si nous examinons les éléments 4 et 5, l'état de la file d'attente sera le suivant:
maintenant la pile de sortie n'est pas vide, et si nous exécutons une opération de série, seulement 3 seront sortis de la pile de sortie. Ensuite, l'état sera vu comme ci-dessous;
encore une fois, si nous exécutons deux autres opérations de série, lors de la première opération de série, file vérifiera si la pile de sortie est vide, ce qui est vrai. Puis sortir les éléments de la pile D'entrée et les pousser vers la pile de sortie jusqu'à ce que la pile d'entrée soit vide, puis l'état de la file d'attente sera comme ci-dessous;
facile à voir, la sortie des deux opérations de la série sera {4, 5}
C - la mise en Œuvre De la File d'attente Construit avec Deux Piles
Voici une implémentation en Java. Je suis ne va pas utiliser la mise en œuvre existante de Stack de sorte que l'exemple ici va réinventer la roue;
C - 1) MyStack classe : Une Simple Pile de mise en Œuvre
public class MyStack<T> {
// inner generic Node class
private class Node<T> {
T data;
Node<T> next;
public Node(T data) {
this.data = data;
}
}
private Node<T> head;
private int size;
public void push(T e) {
Node<T> newElem = new Node(e);
if(head == null) {
head = newElem;
} else {
newElem.next = head;
head = newElem; // new elem on the top of the stack
}
size++;
}
public T pop() {
if(head == null)
return null;
T elem = head.data;
head = head.next; // top of the stack is head.next
size--;
return elem;
}
public int size() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
public void printStack() {
System.out.print("Stack: ");
if(size == 0)
System.out.print("Empty !");
else
for(Node<T> temp = head; temp != null; temp = temp.next)
System.out.printf("%s ", temp.data);
System.out.printf("\n");
}
}
C - 2) Classe MyQueue: mise en place de la file D'attente en utilisant deux piles
public class MyQueue<T> {
private MyStack<T> inputStack; // for enqueue
private MyStack<T> outputStack; // for dequeue
private int size;
public MyQueue() {
inputStack = new MyStack<>();
outputStack = new MyStack<>();
}
public void enqueue(T e) {
inputStack.push(e);
size++;
}
public T dequeue() {
// fill out all the Input if output stack is empty
if(outputStack.isEmpty())
while(!inputStack.isEmpty())
outputStack.push(inputStack.pop());
T temp = null;
if(!outputStack.isEmpty()) {
temp = outputStack.pop();
size--;
}
return temp;
}
public int size() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
}
C - 3) Le Code De Démonstration
public class TestMyQueue {
public static void main(String[] args) {
MyQueue<Integer> queue = new MyQueue<>();
// enqueue integers 1..3
for(int i = 1; i <= 3; i++)
queue.enqueue(i);
// execute 2 dequeue operations
for(int i = 0; i < 2; i++)
System.out.println("Dequeued: " + queue.dequeue());
// enqueue integers 4..5
for(int i = 4; i <= 5; i++)
queue.enqueue(i);
// dequeue the rest
while(!queue.isEmpty())
System.out.println("Dequeued: " + queue.dequeue());
}
}
C-4) Sortie De L'Échantillon
Dequeued: 1
Dequeued: 2
Dequeued: 3
Dequeued: 4
Dequeued: 5
Vous pouvez même simuler une file d'attente en utilisant une seule pile. La seconde pile (temporaire) peut être simulée par la pile d'appels récursifs à la méthode insert.
Le principe reste le même lors de l'insertion d'un nouvel élément dans la file d'attente:
- vous devez transférer des éléments d'une pile à une autre pile temporaire, pour inverser leur ordre.
- Puis poussez le nouvel élément à insérer, sur le temporaire stack
- puis transférer les éléments de nouveau à la pile d'origine
- le nouvel élément sera sur le fond de la pile, et l'élément le plus ancien est sur le dessus (le premier à être poppé)
une classe de file d'attente utilisant une seule pile serait la suivante:
public class SimulatedQueue<E> {
private java.util.Stack<E> stack = new java.util.Stack<E>();
public void insert(E elem) {
if (!stack.empty()) {
E topElem = stack.pop();
insert(elem);
stack.push(topElem);
}
else
stack.push(elem);
}
public E remove() {
return stack.pop();
}
}
Le temps complexités serait pire, si. Une bonne implémentation de la file d'attente fait tout en temps constant.
Modifier
Je ne sais pas pourquoi ma réponse a été rétrogradée ici. Si nous programmons, nous nous soucions de la complexité du temps, et l'utilisation de deux piles standard pour faire une file d'attente est inefficace. C'est un point très valable et pertinent. Si quelqu'un d'autre ressent le besoin de réduire cela, je serais intéressé de savoir pourquoi.
un peu plus de détails : sur pourquoi l'utilisation de deux piles est pire qu'une simple file d'attente: si vous utilisez deux piles, et quelqu'un appelle dequeue alors que la boîte de réception est vide, vous avez besoin de temps linéaire pour aller au fond de la boîte de réception (comme vous pouvez le voir dans le code de Dave).
vous pouvez implémenter une file d'attente comme une liste mono-liée (chaque élément pointe vers l'élément inséré suivant), en gardant un pointeur supplémentaire vers le dernier élément inséré pour les push (ou faire il cyclique de la liste). Implémenter queue et dequeue sur cette structure de données est très facile à faire en temps constant. C'est dans le pire des cas, le temps constant, pas amorti. Et, comme les commentaires semblent demander cette clarification, dans le pire des cas, le temps constant est strictement meilleur que le temps constant amorti.
laisser la file d'attente pour être mis en œuvre être q et les piles utilisées pour mettre en œuvre q être stack1 et stack2.
Q Peut être mis en œuvre dans deux voies:
Méthode 1 (en rendant l'opération de recherche coûteuse)
cette méthode permet de s'assurer que l'élément nouvellement entré est toujours au sommet de la cheminée 1, de sorte que l'opération de laquelle sort tout juste de la cheminée 1. Pour placer l'élément au sommet de la stace1, la stace2 est utilisée.
enQueue(q, x)
1) While stack1 is not empty, push everything from stack1 to stack2.
2) Push x to stack1 (assuming size of stacks is unlimited).
3) Push everything back to stack1.
deQueue(q)
1) If stack1 is empty then error
2) Pop an item from stack1 and return it.
la Méthode 2 (résorption de l'opération coûteuse)
dans cette méthode, en mode de mise en file d'attente, le nouvel élément est entré au haut du stack1. Si la pile 2 est vide, tous les éléments sont déplacés vers la pile 2 et finalement le haut de la pile 2 est retourné.
enQueue(q, x)
1) Push x to stack1 (assuming size of stacks is unlimited).
deQueue(q)
1) If both stacks are empty then error.
2) If stack2 is empty
While stack1 is not empty, push everything from stack1 to stack2.
3) Pop the element from stack2 and return it.
la méthode 2 est certainement meilleure que la méthode 1. La méthode 1 déplace tous les éléments deux fois dans l'opération de recherche, tandis que la méthode 2 (en mode "deQueue") déplace les éléments une fois et ne déplace les éléments que si le stack2 est vide.
une solution en c#
public class Queue<T> where T : class
{
private Stack<T> input = new Stack<T>();
private Stack<T> output = new Stack<T>();
public void Enqueue(T t)
{
input.Push(t);
}
public T Dequeue()
{
if (output.Count == 0)
{
while (input.Count != 0)
{
output.Push(input.Pop());
}
}
return output.Pop();
}
}
deux piles dans la file d'attente sont définies comme stack1 et stack2 .
enquête: Les éléments euqueued sont toujours poussés dans stack1
file d'attente: Le haut de stack2 peut être sorti car il est le premier élément inséré dans la file d'attente quand stack2 n'est pas vide. Lorsque stack2 est vide, nous pop tous les éléments de stack1 et les pousser dans stack2 un par un. Le premier élément d'une file d'attente est poussé dans le bas de la stack1 . Il peut être sorti directement après des opérations de poussée et de poussée puisqu'il se trouve au sommet de la stack2 .
le code suivant est le même C++:
template <typename T> class CQueue
{
public:
CQueue(void);
~CQueue(void);
void appendTail(const T& node);
T deleteHead();
private:
stack<T> stack1;
stack<T> stack2;
};
template<typename T> void CQueue<T>::appendTail(const T& element) {
stack1.push(element);
}
template<typename T> T CQueue<T>::deleteHead() {
if(stack2.size()<= 0) {
while(stack1.size()>0) {
T& data = stack1.top();
stack1.pop();
stack2.push(data);
}
}
if(stack2.size() == 0)
throw new exception("queue is empty");
T head = stack2.top();
stack2.pop();
return head;
}
This la solution est empruntée à mon blog . Une analyse plus détaillée avec des simulations d'opérations étape par étape est disponible sur ma page web blog.
vous aurez à pop tout sur la première pile pour obtenir l'élément inférieur. Remettez-les ensuite sur la deuxième pile pour chaque opération "dequeue".
pour C# developer voici le programme complet:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace QueueImplimentationUsingStack
{
class Program
{
public class Stack<T>
{
public int size;
public Node<T> head;
public void Push(T data)
{
Node<T> node = new Node<T>();
node.data = data;
if (head == null)
head = node;
else
{
node.link = head;
head = node;
}
size++;
Display();
}
public Node<T> Pop()
{
if (head == null)
return null;
else
{
Node<T> temp = head;
//temp.link = null;
head = head.link;
size--;
Display();
return temp;
}
}
public void Display()
{
if (size == 0)
Console.WriteLine("Empty");
else
{
Console.Clear();
Node<T> temp = head;
while (temp!= null)
{
Console.WriteLine(temp.data);
temp = temp.link;
}
}
}
}
public class Queue<T>
{
public int size;
public Stack<T> inbox;
public Stack<T> outbox;
public Queue()
{
inbox = new Stack<T>();
outbox = new Stack<T>();
}
public void EnQueue(T data)
{
inbox.Push(data);
size++;
}
public Node<T> DeQueue()
{
if (outbox.size == 0)
{
while (inbox.size != 0)
{
outbox.Push(inbox.Pop().data);
}
}
Node<T> temp = new Node<T>();
if (outbox.size != 0)
{
temp = outbox.Pop();
size--;
}
return temp;
}
}
public class Node<T>
{
public T data;
public Node<T> link;
}
static void Main(string[] args)
{
Queue<int> q = new Queue<int>();
for (int i = 1; i <= 3; i++)
q.EnQueue(i);
// q.Display();
for (int i = 1; i < 3; i++)
q.DeQueue();
//q.Display();
Console.ReadKey();
}
}
}
// Two stacks s1 Original and s2 as Temp one
private Stack<Integer> s1 = new Stack<Integer>();
private Stack<Integer> s2 = new Stack<Integer>();
/*
* Here we insert the data into the stack and if data all ready exist on
* stack than we copy the entire stack s1 to s2 recursively and push the new
* element data onto s1 and than again recursively call the s2 to pop on s1.
*
* Note here we can use either way ie We can keep pushing on s1 and than
* while popping we can remove the first element from s2 by copying
* recursively the data and removing the first index element.
*/
public void insert( int data )
{
if( s1.size() == 0 )
{
s1.push( data );
}
else
{
while( !s1.isEmpty() )
{
s2.push( s1.pop() );
}
s1.push( data );
while( !s2.isEmpty() )
{
s1.push( s2.pop() );
}
}
}
public void remove()
{
if( s1.isEmpty() )
{
System.out.println( "Empty" );
}
else
{
s1.pop();
}
}
Une mise en œuvre d'une file d'attente à l'aide de deux piles de Swift:
struct Stack<Element> {
var items = [Element]()
var count : Int {
return items.count
}
mutating func push(_ item: Element) {
items.append(item)
}
mutating func pop() -> Element? {
return items.removeLast()
}
func peek() -> Element? {
return items.last
}
}
struct Queue<Element> {
var inStack = Stack<Element>()
var outStack = Stack<Element>()
mutating func enqueue(_ item: Element) {
inStack.push(item)
}
mutating func dequeue() -> Element? {
fillOutStack()
return outStack.pop()
}
mutating func peek() -> Element? {
fillOutStack()
return outStack.peek()
}
private mutating func fillOutStack() {
if outStack.count == 0 {
while inStack.count != 0 {
outStack.push(inStack.pop()!)
}
}
}
}
alors que vous obtiendrez beaucoup de messages liés à la mise en œuvre d'une file d'attente avec deux piles : 1. Soit en rendant le processus d'enquête beaucoup plus coûteux 2. Ou en faisant la file d'attente de processus beaucoup plus coûteux
https://www.geeksforgeeks.org/queue-using-stacks /
une façon importante que j'ai découvert à partir du post ci-dessus était de construire la file d'attente avec seulement la structure de données de la pile et la pile d'appels de récursion.
alors que l'on peut dire que littéralement ceci utilise encore deux cheminées, mais alors idéalement ceci utilise seulement une structure de données de pile.
voici l'explication du problème:
-
déclarez une seule pile pour la recherche et la destruction des données et poussez les données dans la pile.
-
pendant le dégel ont une condition de base où l'élément de la pile est poped lorsque le la taille de la pile est 1. Cela permettra de s'assurer qu'il n'y a pas de débordement de la pile pendant la récursion de la deQueue.
-
pendant que deQueueing pop d'abord les données du haut de la pile. Idéalement, cet élément sera l'élément qui est présent en haut de la pile. Maintenant, une fois que cela est fait, appeler récursivement la fonction deQueue puis pousser l'élément placé au-dessus de nouveau dans la pile.
le code aura l'air comme ci-dessous:
if (s1.isEmpty())
System.out.println("The Queue is empty");
else if (s1.size() == 1)
return s1.pop();
else {
int x = s1.pop();
int result = deQueue();
s1.push(x);
return result;
de cette façon, vous pouvez créer une file d'attente en utilisant une structure de données de pile unique et la pile d'appels de récursion.
public class QueueUsingStacks<T>
{
private LinkedListStack<T> stack1;
private LinkedListStack<T> stack2;
public QueueUsingStacks()
{
stack1=new LinkedListStack<T>();
stack2 = new LinkedListStack<T>();
}
public void Copy(LinkedListStack<T> source,LinkedListStack<T> dest )
{
while(source.Head!=null)
{
dest.Push(source.Head.Data);
source.Head = source.Head.Next;
}
}
public void Enqueue(T entry)
{
stack1.Push(entry);
}
public T Dequeue()
{
T obj;
if (stack2 != null)
{
Copy(stack1, stack2);
obj = stack2.Pop();
Copy(stack2, stack1);
}
else
{
throw new Exception("Stack is empty");
}
return obj;
}
public void Display()
{
stack1.Display();
}
}
pour chaque opération de recherche, nous ajoutons au haut du stack1. Pour chaque quantité, nous vidons le contenu de la stac1 dans la stac2, et supprimons l'élément en haut de la pile.La complexité temporelle est O (n) pour dequeue, puisque nous devons copier la stack1 à la stack2. la complexité temporelle de l'enquête est la même que celle d'une pile régulière
je vais répondre à cette question dans Go parce que Go n'a pas beaucoup de collections dans sa bibliothèque standard.
Puisqu'une pile est vraiment facile à mettre en œuvre, j'ai pensé que je pourrais essayer d'utiliser deux piles pour accomplir une file d'attente double extrémité. Pour mieux comprendre comment j'en suis arrivé à ma réponse, j'ai divisé la mise en œuvre en deux parties, la première partie est peut-être plus facile à comprendre, mais elle est incomplète.
type IntQueue struct {
front []int
back []int
}
func (q *IntQueue) PushFront(v int) {
q.front = append(q.front, v)
}
func (q *IntQueue) Front() int {
if len(q.front) > 0 {
return q.front[len(q.front)-1]
} else {
return q.back[0]
}
}
func (q *IntQueue) PopFront() {
if len(q.front) > 0 {
q.front = q.front[:len(q.front)-1]
} else {
q.back = q.back[1:]
}
}
func (q *IntQueue) PushBack(v int) {
q.back = append(q.back, v)
}
func (q *IntQueue) Back() int {
if len(q.back) > 0 {
return q.back[len(q.back)-1]
} else {
return q.front[0]
}
}
func (q *IntQueue) PopBack() {
if len(q.back) > 0 {
q.back = q.back[:len(q.back)-1]
} else {
q.front = q.front[1:]
}
}
c'est essentiellement deux piles où nous permettons que le fond des piles soit manipulé l'un par l'autre. J'ai aussi utilisé les conventions de nommage STL, où les opérations traditionnelles push, pop, peek d'une pile ont un préfixe front/back qu'elles se réfèrent à l'avant ou à l'arrière de la file d'attente.
le problème avec le code ci-dessus est qu'il n'utilise pas la mémoire très efficacement. En fait, ça pousse sans fin jusqu'à ce que tu manques d'espace. C'est vraiment mauvais. Le correctif pour cela est de simplement réutiliser le fond de la pile de l'espace à chaque fois que possible. Nous devons introduire un offset pour suivre cela car une tranche de Go ne peut pas pousser à l'avant une fois rétrécie.
type IntQueue struct {
front []int
frontOffset int
back []int
backOffset int
}
func (q *IntQueue) PushFront(v int) {
if q.backOffset > 0 {
i := q.backOffset - 1
q.back[i] = v
q.backOffset = i
} else {
q.front = append(q.front, v)
}
}
func (q *IntQueue) Front() int {
if len(q.front) > 0 {
return q.front[len(q.front)-1]
} else {
return q.back[q.backOffset]
}
}
func (q *IntQueue) PopFront() {
if len(q.front) > 0 {
q.front = q.front[:len(q.front)-1]
} else {
if len(q.back) > 0 {
q.backOffset++
} else {
panic("Cannot pop front of empty queue.")
}
}
}
func (q *IntQueue) PushBack(v int) {
if q.frontOffset > 0 {
i := q.frontOffset - 1
q.front[i] = v
q.frontOffset = i
} else {
q.back = append(q.back, v)
}
}
func (q *IntQueue) Back() int {
if len(q.back) > 0 {
return q.back[len(q.back)-1]
} else {
return q.front[q.frontOffset]
}
}
func (q *IntQueue) PopBack() {
if len(q.back) > 0 {
q.back = q.back[:len(q.back)-1]
} else {
if len(q.front) > 0 {
q.frontOffset++
} else {
panic("Cannot pop back of empty queue.")
}
}
}
c'est beaucoup de petites fonctions mais des 6 Fonctions 3 d'entre elles sont juste des miroirs de l'autre.
voici ma solution en java en utilisant linkedlist.
class queue<T>{
static class Node<T>{
private T data;
private Node<T> next;
Node(T data){
this.data = data;
next = null;
}
}
Node firstTop;
Node secondTop;
void push(T data){
Node temp = new Node(data);
temp.next = firstTop;
firstTop = temp;
}
void pop(){
if(firstTop == null){
return;
}
Node temp = firstTop;
while(temp != null){
Node temp1 = new Node(temp.data);
temp1.next = secondTop;
secondTop = temp1;
temp = temp.next;
}
secondTop = secondTop.next;
firstTop = null;
while(secondTop != null){
Node temp3 = new Node(secondTop.data);
temp3.next = firstTop;
firstTop = temp3;
secondTop = secondTop.next;
}
}
}
Note: dans ce cas, l'opération pop prend beaucoup de temps. Je ne suggère donc pas de créer une file d'attente en utilisant deux piles.
Avec O(1) dequeue() , qui est la même que pythonquick réponse :
// time: O(n), space: O(n)
enqueue(x):
if stack.isEmpty():
stack.push(x)
return
temp = stack.pop()
enqueue(x)
stack.push(temp)
// time: O(1)
x dequeue():
return stack.pop()
avec O(1) enqueue() (ceci n'est pas mentionné dans ce post donc cette réponse), qui utilise également le backtracking pour gonfler et retourner l'article le plus bas.
// O(1)
enqueue(x):
stack.push(x)
// time: O(n), space: O(n)
x dequeue():
temp = stack.pop()
if stack.isEmpty():
x = temp
else:
x = dequeue()
stack.push(temp)
return x
évidemment, c'est un bon exercice de codage car il est inefficace mais élégant néanmoins.
mise en file d'attente utilisant deux java.util.Empiler des objets:
public final class QueueUsingStacks<E> {
private final Stack<E> iStack = new Stack<>();
private final Stack<E> oStack = new Stack<>();
public void enqueue(E e) {
iStack.push(e);
}
public E dequeue() {
if (oStack.isEmpty()) {
if (iStack.isEmpty()) {
throw new NoSuchElementException("No elements present in Queue");
}
while (!iStack.isEmpty()) {
oStack.push(iStack.pop());
}
}
return oStack.pop();
}
public boolean isEmpty() {
if (oStack.isEmpty() && iStack.isEmpty()) {
return true;
}
return false;
}
public int size() {
return iStack.size() + oStack.size();
}
}