Comment gérer les contraintes limites lors de l'utilisation de `nls.lm ' in R
j'ai demandé à cette question il y a un moment. Je ne sais pas si je dois poster ceci comme réponse ou une nouvelle question. Je n'ai pas de réponse mais j'ai "résolu" le problème en appliquant L'algorithme de Levenberg-Marquardt en utilisant nls.lm dans R et quand la solution est à la limite, j'exécute l'algorithme de réflexion de la région de confiance (TRR, implémenté dans R) pour m'en écarter. Maintenant, j'ai de nouvelles questions.
D'après mon expérience, en faisant cela le programme atteint de façon optimale et n'est pas si sensible aux valeurs de départ. Mais il s'agit seulement d'une méthode pratique pour sortir des problèmes que je rencontre en utilisant nls.lm et aussi d'autres fonctions d'optimisation dans R. Je voudrais savoir pourquoi nls.lm se comporte de cette façon pour les problèmes d'optimisation avec des contraintes aux limites et comment gérer les contraintes aux limites en utilisant nls.lm dans la pratique.
ci-après, j'ai donné un exemple illustrant les deux numéros en utilisant nls.lm .
- Il est sensible aux valeurs de départ.
- il s'arrête quand un paramètre atteint la limite.
A Reproductible Example: Focus Dataset D
library(devtools)
install_github("KineticEval","zhenglei-gao")
library(KineticEval)
data(FOCUS2006D)
km <- mkinmod.full(parent=list(type="SFO",M0 = list(ini = 0.1,fixed = 0,lower = 0.0,upper =Inf),to="m1"),m1=list(type="SFO"),data=FOCUS2006D)
system.time(Fit.TRR <- KinEval(km,evalMethod = 'NLLS',optimMethod = 'TRR'))
system.time(Fit.LM <- KinEval(km,evalMethod = 'NLLS',optimMethod = 'LM',ctr=kingui.control(runTRR=FALSE)))
compare_multi_kinmod(km,rbind(Fit.TRR$par,Fit.LM$par))
dev.print(jpeg,"LMvsTRR.jpeg",width=480)
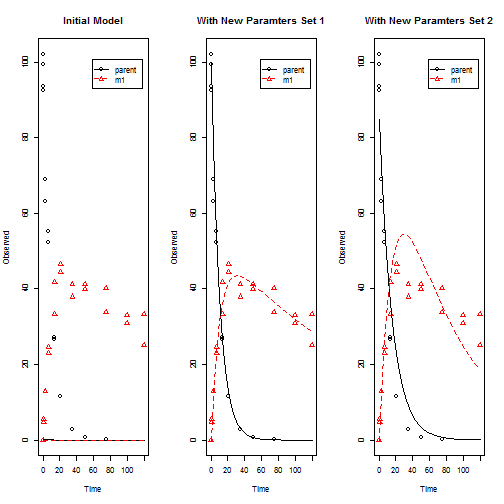
les équations différentielles qui décrivent le modèle / système est:
"d_parent = - k_parent * parent"
"d_m1 = - k_m1 * m1 + k_parent * f_parent_to_m1 * parent"
Dans le graphique de gauche est le modèle avec les valeurs initiales, et au milieu est le modèle ajusté en utilisant " TRR "(similaire à l'algorithme dans la fonction lsqnonlin de Matlab ), à droite est le modèle ajusté en utilisant" LM "avec nls.lm . En regardant les paramètres ajustés ( Fit.LM$par ) vous trouverez qu'un paramètre ajusté ( f_parent_to_m1 ) est à la limite 1 . Si je change la valeur de départ pour un paramètre M0_parent de 0.1 à 100, alors j'obtiens les mêmes résultats avec nls.lm et lsqnonlin .Je avoir de nombreux cas comme celui-ci.
newpars <- rbind(Fit.TRR$par,Fit.LM$par)
rownames(newpars)<- c("TRR(lsqnonlin)","LM(nls.lm)")
newpars
M0_parent k_parent k_m1 f_parent_to_m1
TRR(lsqnonlin) 99.59848 0.09869773 0.005260654 0.514476
LM(nls.lm) 84.79150 0.06352110 0.014783294 1.000000
sauf pour les problèmes ci-dessus, il arrive souvent que le Hessian retourné par nls.lm n'est pas inversible(surtout quand certains paramètres sont à la limite) de sorte que je ne peux pas obtenir une estimation de la matrice de covariance. D'autre part, L'algorithme" TRR " (dans Matlab) donne presque toujours une estimation en calculant le Jacobien au point de solution. Je pense que C'est utile, mais je suis aussi sûr que l'optimisation R les algorithmes (ceux que j'ai essayés) n'ont pas fait cela pour une raison. J'aimerais savoir si je me trompe en utilisant la méthode de Matlab pour calculer la matrice de covariance afin d'obtenir l'erreur-type pour les estimations des paramètres.
une dernière note, j'ai affirmé dans mon post précédent que le Matlab lsqnonlin surpasse les fonctions d'optimisation de R dans presque tous les cas. J'ai eu tort. L'algorithme" Trust-Region-Reflective " utilisé dans Matlab est en fait plus lent (parfois beaucoup plus lent) s'il est aussi implémenté dans R comme vous pouvez le voir dans l'exemple ci-dessus. Cependant, il est encore plus stable et atteint une meilleure solution que les algorithmes d'optimisation de base du R.
2 réponses
tout d'abord, je ne suis pas un expert en Matlab et Optimisation et je N'ai jamais utilisé R.
Je ne suis pas sûr de voir ce qu'est votre question actuelle, mais peut-être que je peux apporter un peu de lumière dans votre puzzle:
LM est légèrement améliorée Gauß-Newton, l'approche des problèmes avec plusieurs minima locaux, il est très sensible aux conditions initiales. Le fait d'inclure des limites génère généralement plus de ces minimums.
TRR est proche de LM, mais plus robuste. Il a de meilleures capacités pour "sauter hors de" mauvais minima locaux. Il est tout à fait possible qu'il se comporte mieux, mais moins bon qu'un LM. En fait, expliquer pourquoi est très difficile. Vous devez étudier les algorithmes en détail et de regarder comment ils se comportent dans cette situation.
Je ne peux pas expliquer la différence entre la mise en œuvre de Matlab et de R, mais il y a plusieurs extensions à TRR que Matlab utilise peut-être et R ne le fait pas. Votre approche de L'utilisation de LM et que TRR converge alternativement mieux que TRR seul?
en utilisant le paquet mkin, vous pouvez trouver les paramètres en utilisant l'algorithme "Port" (qui est aussi une sorte d'algorithme TRR d'après ce que j'ai pu voir dans sa documentation), ou l'algorithme "Marq", qui utilise nls.lm en arrière-plan. Vous pouvez alors utiliser des valeurs de départ" normales" ou "mauvaises".
library(mkin)
packageVersion("mkin")
version récente mkin peut accélérer le processus considérablement car ils compilent les modèles à partir du code C généré automatiquement si un compilateur est disponible sur votre système (par exemple, vous avez R-base-dev installé sur Debian/Ubuntu, ou Rtools sur Windows).
définit le modèle:
m <- mkinmod(parent = mkinsub("SFO", "m1"),
m1 = mkinsub("SFO"),
use_of_ff = "max")
vous pouvez vérifier que les équations différentielles sont correctes:
cat(m$diffs, sep = "\n")
alors nous nous adaptons en quatre variantes, Port et LM, avec ou sans M0 fixé à 0.1:
f.Port = mkinfit(m, FOCUS_2006_D)
f.Port.M0 = mkinfit(m, FOCUS_2006_D, state.ini = c(parent = 0.1, m1 = 0))
f.LM = mkinfit(m, FOCUS_2006_D, method.modFit = "Marq")
f.LM.M0 = mkinfit(m, FOCUS_2006_D, state.ini = c(parent = 0.1, m1 = 0),
method.modFit = "Marq")
ensuite, nous regardons les résultats:
results <- sapply(list(Port = f.Port, Port.M0 = f.Port.M0, LM = f.LM, LM.M0 = f.LM.M0),
function(x) round(summary(x)$bpar[, "Estimate"], 5))
qui sont
Port Port.M0 LM LM.M0
parent_0 99.59848 99.59848 99.59848 39.52278
k_parent 0.09870 0.09870 0.09870 0.00000
k_m1 0.00526 0.00526 0.00526 0.00000
f_parent_to_m1 0.51448 0.51448 0.51448 1.00000
donc nous pouvons voir que l'algorithme de Port trouve la meilleure solution (au meilleur de ma connaissance) même avec de mauvaises valeurs de départ. La question de la vitesse que l'on peut avoir avec des modèles plus compliqués est atténuée en utilisant la génération automatique de C code.