Comment trouver la fréquence fondamentale d'un son de cordes de guitare?

vous pouvez utiliser l'autocorrélation du signal, qui est la transformation inverse de la magnitude au carré du DFT. Si vous échantillonnez à 44100 échantillons / s, alors une fondamentale de 82,4 Hz est d'environ 535 échantillons, tandis que 1479,98 Hz est d'environ 30 échantillons. Cherchez le décalage positif de pointe dans cette plage (par exemple de 28 à 560). Assurez-vous que votre fenêtre est au moins deux périodes de la plus fondamentale, qui serait 1070 échantillons ici. Au pouvoir suivant de deux, c'est un tampon de 2048 échantillons. Pour une meilleure fréquence résolution et une moins estimation biaisée, utiliser un tampon plus, mais pas tant que le signal n'est plus environ stationnaire. Voici un exemple en Python:

from pylab import *
import wave

fs = 44100.0   # sample rate
K = 3          # number of windows
L = 8192       # 1st pass window overlap, 50%
M = 16384      # 1st pass window length
N = 32768      # 1st pass DFT lenth: acyclic correlation

# load a sample of guitar playing an open string 6
# with a fundamental frequency of 82.4 Hz (in theory),
# but this sample is actually at about 81.97 Hz
g = fromstring(wave.open('dist_gtr_6.wav').readframes(-1),
               dtype='int16')
g = g / float64(max(abs(g)))    # normalize to +/- 1.0
mi = len(g) / 4                 # start index

def welch(x, w, L, N):
    # Welch's method
    M = len(w)
    K = (len(x) - L) / (M - L)
    Xsq = zeros(N/2+1)                  # len(N-point rfft) = N/2+1
    for k in range(K):
        m = k * ( M - L)
        xt = w * x[m:m+M]
        # use rfft for efficiency (assumes x is real-valued)
        Xsq = Xsq + abs(rfft(xt, N)) ** 2
    Xsq = Xsq / K
    Wsq = abs(rfft(w, N)) ** 2
    bias = irfft(Wsq)                   # for unbiasing Rxx and Sxx
    p = dot(x,x) / len(x)               # avg power, used as a check
    return Xsq, bias, p

# first pass: acyclic autocorrelation
x = g[mi:mi + K*M - (K-1)*L]        # len(x) = 32768
w = hamming(M)                      # hamming[m] = 0.54 - 0.46*cos(2*pi*m/M)
                                    # reduces the side lobes in DFT
Xsq, bias, p = welch(x, w, L, N)
Rxx = irfft(Xsq)                    # acyclic autocorrelation
Rxx = Rxx / bias                    # unbias (bias is tapered)
mp = argmax(Rxx[28:561]) + 28       # index of 1st peak in 28 to 560

# 2nd pass: cyclic autocorrelation
N = M = L - (L % mp)                # window an integer number of periods
                                    # shortened to ~8192 for stationarity
x = g[mi:mi+K*M]                    # data for K windows
w = ones(M); L = 0                  # rectangular, non-overlaping
Xsq, bias, p = welch(x, w, L, N)
Rxx = irfft(Xsq)                    # cyclic autocorrelation
Rxx = Rxx / bias                    # unbias (bias is constant)
mp = argmax(Rxx[28:561]) + 28       # index of 1st peak in 28 to 560

Sxx = Xsq / bias[0]
Sxx[1:-1] = 2 * Sxx[1:-1]           # fold the freq axis
Sxx = Sxx / N                       # normalize S for avg power
n0 = N / mp
np = argmax(Sxx[n0-2:n0+3]) + n0-2  # bin of the nearest peak power

# check
print "\nAverage Power"
print "  p:", p
print "Rxx:", Rxx[0]                # should equal dot product, p
print "Sxx:", sum(Sxx), '\n'        # should equal Rxx[0]

figure().subplots_adjust(hspace=0.5)
subplot2grid((2,1), (0,0))
title('Autocorrelation, R$_{xx}$'); xlabel('Lags')
mr = r_[:3 * mp]
plot(Rxx[mr]); plot(mp, Rxx[mp], 'ro')
xticks(mp/2 * r_[1:6])
grid(); axis('tight'); ylim(1.25*min(Rxx), 1.25*max(Rxx))

subplot2grid((2,1), (1,0))
title('Power Spectral Density, S$_{xx}$'); xlabel('Frequency (Hz)')
fr = r_[:5 * np]; f = fs * fr / N; 
vlines(f, 0, Sxx[fr], colors='b', linewidth=2)
xticks((fs * np/N  * r_[1:5]).round(3))
grid(); axis('tight'); ylim(0,1.25*max(Sxx[fr]))
show()

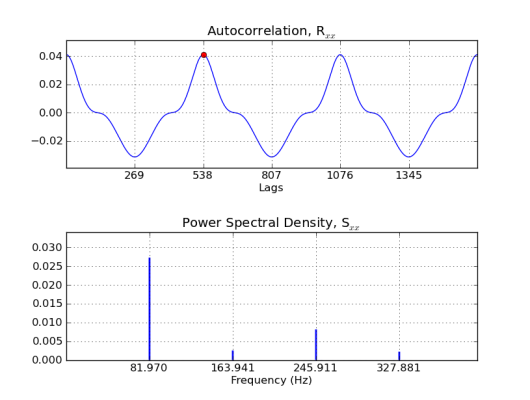
Sortie:

Average Power
  p: 0.0410611012542
Rxx: 0.0410611012542
Sxx: 0.0410611012542 

Edit: mise à jour pour utiliser la méthode de Welch pour estimer l'autocorrélation. Le chevauchement des fenêtres compense la fenêtre de martelage. Je calcule aussi le biais conique de la fenêtre de martelage pour dénouer l'autocorrélation.

Edit: ajout d'une 2e passe avec cyclique corrélation pour nettoyer la densité spectrale de puissance. Cette passe utilise 3 fenêtres rectangulaires sans chevauchement 538*15 = 8070 (assez courtes pour être presque stationnaires). Le biais pour la corrélation cyclique est une constante, au lieu du biais conique de la fenêtre de martelage.