Comment filtrer les données FFT (pour la visualisation audio)?
je la regardais Web Audio API demo partie ce beau livre
si vous regardez la démo, les pics FFT tombent en douceur. J'essaie de faire la même chose avec le traitement en mode Java en utilisant la bibliothèque minim. J'ai regardé comment cela se fait avec l'api web audio dans le doFFTAnalysis () méthode et essayé de répliquer avec minim. J'ai aussi essayé de porter comment abs() fonctionne avec le type complexe:
/ 26.2.7/3 abs(__z): Returns the magnitude of __z.
00565 template<typename _Tp>
00566 inline _Tp
00567 __complex_abs(const complex<_Tp>& __z)
00568 {
00569 _Tp __x = __z.real();
00570 _Tp __y = __z.imag();
00571 const _Tp __s = std::max(abs(__x), abs(__y));
00572 if (__s == _Tp()) // well ...
00573 return __s;
00574 __x /= __s;
00575 __y /= __s;
00576 return __s * sqrt(__x * __x + __y * __y);
00577 }
00578
je suis actuellement en train de faire un prototype rapide en utilisant le traitement(un cadre/bibliothèque java). Mon code ressemble à ceci:
import ddf.minim.*;
import ddf.minim.analysis.*;
private int blockSize = 512;
private Minim minim;
private AudioInput in;
private FFT mfft;
private float[] time = new float[blockSize];//time domain
private float[] real = new float[blockSize];
private float[] imag = new float[blockSize];
private float[] freq = new float[blockSize];//smoothed freq. domain
public void setup() {
minim = new Minim(this);
in = minim.getLineIn(Minim.STEREO, blockSize);
mfft = new FFT( in.bufferSize(), in.sampleRate() );
}
public void draw() {
background(255);
for (int i = 0; i < blockSize; i++) time[i] = in.left.get(i);
mfft.forward( time);
real = mfft.getSpectrumReal();
imag = mfft.getSpectrumImaginary();
final float magnitudeScale = 1.0 / mfft.specSize();
final float k = (float)mouseX/width;
for (int i = 0; i < blockSize; i++)
{
float creal = real[i];
float cimag = imag[i];
float s = Math.max(creal,cimag);
creal /= s;
cimag /= s;
float absComplex = (float)(s * Math.sqrt(creal*creal + cimag*cimag));
float scalarMagnitude = absComplex * magnitudeScale;
freq[i] = (k * mfft.getBand(i) + (1 - k) * scalarMagnitude);
line( i, height, i, height - freq[i]*8 );
}
fill(0);
text("smoothing: " + k,10,10);
}
Je n'obtiens pas d'erreurs, ce qui est bon, mais je n'obtiens pas le comportement attendu qui est mauvais. Je m'attendais à ce que les pics tombent plus lentement quand lissage (k) est proche 1, mais aussi loin que je peux dire mon code seulement les échelles les bandes.
malheureusement, les maths et le son ne sont pas mon point fort, donc je poignarde dans le noir. Comment puis-je répliquer la belle visualisation à partir de la démo de L'API Audio Web ?
je serais tenté de dire qu'il peut s'agir de langage agnostique, mais utiliser javascript par exemple ne s'appliquerait pas :). Cependant, je suis heureux d'essayer toute autre bibliothèque java qui fait l'analyse FFT.
UPDATE
j'ai une solution simple pour lisser (diminuer continuellement les valeurs de chaque bande FFT précédente si la bande FFT actuelle n'est pas plus élevée:
import ddf.minim.analysis.*;
import ddf.minim.*;
Minim minim;
AudioInput in;
FFT fft;
float smoothing = 0;
float[] fftReal;
float[] fftImag;
float[] fftSmooth;
int specSize;
void setup(){
size(640, 360, P3D);
minim = new Minim(this);
in = minim.getLineIn(Minim.STEREO, 512);
fft = new FFT(in.bufferSize(), in.sampleRate());
specSize = fft.specSize();
fftSmooth = new float[specSize];
fftReal = new float[specSize];
colorMode(HSB,specSize,100,100);
}
void draw(){
background(0);
stroke(255);
fft.forward( in.left);
fftReal = fft.getSpectrumReal();
fftImag = fft.getSpectrumImaginary();
for(int i = 0; i < specSize; i++)
{
float band = fft.getBand(i);
fftSmooth[i] *= smoothing;
if(fftSmooth[i] < band) fftSmooth[i] = band;
stroke(i,100,50);
line( i, height, i, height - fftSmooth[i]*8 );
stroke(i,100,100);
line( i, height, i, height - band*8 );
}
text("smoothing: " + (int)(smoothing*100),10,10);
}
void keyPressed(){
float inc = 0.01;
if(keyCode == UP && smoothing < 1-inc) smoothing += inc;
if(keyCode == DOWN && smoothing > inc) smoothing -= inc;
}

le délavé le graphe est le lissé et le complètement saturé est le vivant.
je manque cependant quelque chose par rapport à la démo de L'API Audio Web:
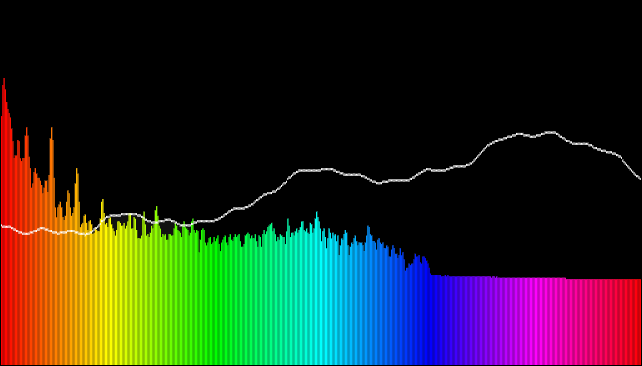
je pense que L'API Audio Web pourrait tenir compte du fait que les fréquences moyennes et supérieures devront être ajustées pour être plus proches de ce que nous percevons, mais je ne suis pas sûr de la façon d'aborder cela.
j'essayais de lire plus sur la façon dont la classe RealtimeAnalyser fait cela pour le WebAudioAPI, mais il semble FFTFrame classdoFFT méthode pourrait faire l'échelle logarithmique. Je n'ai pas encore compris comment doFFT fonctionne.
Comment puis-je mettre à l'échelle un graphique TNI brut avec une échelle logarithmique pour tenir compte de la perception ? Mon objectif est de faire un décent à la recherche de visualisation, et je suppose que j'ai besoin de:
- lisse les valeurs, sinon les éléments s'animeront rapide/crispés
- échelle la FFT bacs/bandes d'obtenir de meilleures données pour les moyennes/hautes fréquences
- carte traiter les valeurs FFT en éléments visuels (trouver les valeurs/limites maximales)
y a-t-il des conseils pour y arriver ?
UPDATE 2
je suppose que cette partie fait le lissage et la mise à l'échelle que je suis après dans L'API Audio Web: // Normaliser de façon à obtenir une onde sinusoïdale d'entrée à 0dBfs s'enregistre comme 0dBfs (défauf FFT scaling factor). const double magnitudeScale = 1.0 / DefaultFFTSize;
// A value of 0 does no averaging with the previous result. Larger values produce slower, but smoother changes.
double k = m_smoothingTimeConstant;
k = max(0.0, k);
k = min(1.0, k);
// Convert the analysis data from complex to magnitude and average with the previous result.
float* destination = magnitudeBuffer().data();
size_t n = magnitudeBuffer().size();
for (size_t i = 0; i < n; ++i) {
Complex c(realP[i], imagP[i]);
double scalarMagnitude = abs(c) * magnitudeScale;
destination[i] = float(k * destination[i] + (1 - k) * scalarMagnitude);
}
il semble que la mise à l'échelle se fait en prenant l'absolu de la valeur complexe. Ce post indique la même direction. J'ai essayé d'utiliser l'abs du nombre complexe en utilisant Minim et en utilisant diverses fonctions de fenêtre, mais il ne ressemble toujours pas à ce que je vise(le Web Audio API demo):
import ddf.minim.analysis.*;
import ddf.minim.*;
Minim minim;
AudioInput in;
FFT fft;
float smoothing = 0;
float[] fftReal;
float[] fftImag;
float[] fftSmooth;
int specSize;
WindowFunction[] window = {FFT.NONE,FFT.HAMMING,FFT.HANN,FFT.COSINE,FFT.TRIANGULAR,FFT.BARTLETT,FFT.BARTLETTHANN,FFT.LANCZOS,FFT.BLACKMAN,FFT.GAUSS};
String[] wlabel = {"NONE","HAMMING","HANN","COSINE","TRIANGULAR","BARTLETT","BARTLETTHANN","LANCZOS","BLACKMAN","GAUSS"};
int windex = 0;
void setup(){
size(640, 360, P3D);
minim = new Minim(this);
in = minim.getLineIn(Minim.STEREO, 512);
fft = new FFT(in.bufferSize(), in.sampleRate());
fft.window(window[windex]);
specSize = fft.specSize();
fftSmooth = new float[specSize];
fftReal = new float[specSize];
colorMode(HSB,specSize,100,100);
}
void draw(){
background(0);
stroke(255);
fft.forward( in.mix);
fftReal = fft.getSpectrumReal();
fftImag = fft.getSpectrumImaginary();
for(int i = 0; i < specSize; i++)
{
float band = fft.getBand(i);
//Sw = abs(Sw(1:(1+N/2))); %# abs is sqrt(real^2 + imag^2)
float abs = sqrt(fftReal[i]*fftReal[i] + fftImag[i]*fftImag[i]);
fftSmooth[i] *= smoothing;
if(fftSmooth[i] < abs) fftSmooth[i] = abs;
stroke(i,100,50);
line( i, height, i, height - fftSmooth[i]*8 );
stroke(i,100,100);
line( i, height, i, height - band*8 );
}
text("smoothing: " + (int)(smoothing*100)+"nwindow:"+wlabel[windex],10,10);
}
void keyPressed(){
float inc = 0.01;
if(keyCode == UP && smoothing < 1-inc) smoothing += inc;
if(keyCode == DOWN && smoothing > inc) smoothing -= inc;
if(key == 'W' && windex < window.length-1) windex++;
if(key == 'w' && windex > 0) windex--;
if(key == 'w' || key == 'W') fft.window(window[windex]);
}
je ne suis pas sûr que je suis utiliser les fonctions de fenêtre correctement parce que je ne remarque pas une énorme différence entre eux. Est l'abs de la valeur complexe correct ? Comment puis-je obtenir une visualisation plus proche de mon objectif ?
UPDATE 3
j'ai essayé d'appliquer les conseils utiles de @wakjah comme ceci:
import ddf.minim.analysis.*;
import ddf.minim.*;
Minim minim;
AudioInput in;
FFT fft;
float smoothing = 0;
float[] fftReal;
float[] fftImag;
float[] fftSmooth;
float[] fftPrev;
float[] fftCurr;
int specSize;
WindowFunction[] window = {FFT.NONE,FFT.HAMMING,FFT.HANN,FFT.COSINE,FFT.TRIANGULAR,FFT.BARTLETT,FFT.BARTLETTHANN,FFT.LANCZOS,FFT.BLACKMAN,FFT.GAUSS};
String[] wlabel = {"NONE","HAMMING","HANN","COSINE","TRIANGULAR","BARTLETT","BARTLETTHANN","LANCZOS","BLACKMAN","GAUSS"};
int windex = 0;
int scale = 10;
void setup(){
minim = new Minim(this);
in = minim.getLineIn(Minim.STEREO, 512);
fft = new FFT(in.bufferSize(), in.sampleRate());
fft.window(window[windex]);
specSize = fft.specSize();
fftSmooth = new float[specSize];
fftPrev = new float[specSize];
fftCurr = new float[specSize];
size(specSize, specSize/2);
colorMode(HSB,specSize,100,100);
}
void draw(){
background(0);
stroke(255);
fft.forward( in.mix);
fftReal = fft.getSpectrumReal();
fftImag = fft.getSpectrumImaginary();
for(int i = 0; i < specSize; i++)
{
//float band = fft.getBand(i);
//Sw = abs(Sw(1:(1+N/2))); %# abs is sqrt(real^2 + imag^2)
//float abs = sqrt(fftReal[i]*fftReal[i] + fftImag[i]*fftImag[i]);
//fftSmooth[i] *= smoothing;
//if(fftSmooth[i] < abs) fftSmooth[i] = abs;
//x_dB = 10 * log10(real(x) ^ 2 + imag(x) ^ 2);
fftCurr[i] = scale * (float)Math.log10(fftReal[i]*fftReal[i] + fftImag[i]*fftImag[i]);
//Y[k] = alpha * Y_(t-1)[k] + (1 - alpha) * X[k]
fftSmooth[i] = smoothing * fftPrev[i] + ((1 - smoothing) * fftCurr[i]);
fftPrev[i] = fftCurr[i];//
stroke(i,100,100);
line( i, height, i, height - fftSmooth[i]);
}
text("smoothing: " + (int)(smoothing*100)+"nwindow:"+wlabel[windex]+"nscale:"+scale,10,10);
}
void keyPressed(){
float inc = 0.01;
if(keyCode == UP && smoothing < 1-inc) smoothing += inc;
if(keyCode == DOWN && smoothing > inc) smoothing -= inc;
if(key == 'W' && windex < window.length-1) windex++;
if(key == 'w' && windex > 0) windex--;
if(key == 'w' || key == 'W') fft.window(window[windex]);
if(keyCode == LEFT && scale > 1) scale--;
if(keyCode == RIGHT) scale++;
}
Je ne suis pas sûr d'avoir appliqué les indices comme prévu. Voici comment ma sortie de l'air:
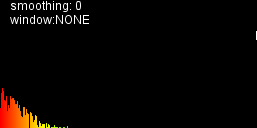
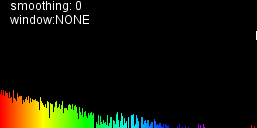
mais Je ne pense pas que je suis là, mais si je compare cela avec des visualisations je vise:
spectre dans windows media player
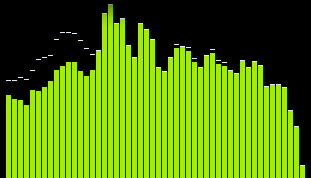
spectre dans le lecteur VLC
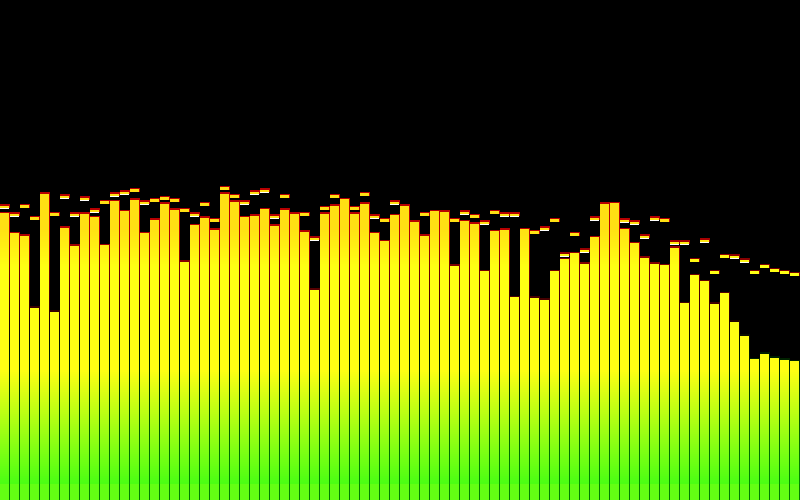
Je ne suis pas sûr d'avoir appliqué correctement l'échelle logarithmique. Mes hypothèses étaient, que je voudrais un tracé similaire à ce que je vise pour après avoir utilisé log10 (ignorant lissage pour le moment).
mise à jour 4:
import ddf.minim.analysis.*;
import ddf.minim.*;
Minim minim;
AudioInput in;
FFT fft;
float smoothing = 0;
float[] fftReal;
float[] fftImag;
float[] fftSmooth;
float[] fftPrev;
float[] fftCurr;
int specSize;
WindowFunction[] window = {FFT.NONE,FFT.HAMMING,FFT.HANN,FFT.COSINE,FFT.TRIANGULAR,FFT.BARTLETT,FFT.BARTLETTHANN,FFT.LANCZOS,FFT.BLACKMAN,FFT.GAUSS};
String[] wlabel = {"NONE","HAMMING","HANN","COSINE","TRIANGULAR","BARTLETT","BARTLETTHANN","LANCZOS","BLACKMAN","GAUSS"};
int windex = 0;
int scale = 10;
void setup(){
minim = new Minim(this);
in = minim.getLineIn(Minim.STEREO, 512);
fft = new FFT(in.bufferSize(), in.sampleRate());
fft.window(window[windex]);
specSize = fft.specSize();
fftSmooth = new float[specSize];
fftPrev = new float[specSize];
fftCurr = new float[specSize];
size(specSize, specSize/2);
colorMode(HSB,specSize,100,100);
}
void draw(){
background(0);
stroke(255);
fft.forward( in.mix);
fftReal = fft.getSpectrumReal();
fftImag = fft.getSpectrumImaginary();
for(int i = 0; i < specSize; i++)
{
float maxVal = Math.max(Math.abs(fftReal[i]), Math.abs(fftImag[i]));
if (maxVal != 0.0f) { // prevent divide-by-zero
// Normalize
fftReal[i] = fftReal[i] / maxVal;
fftImag[i] = fftImag[i] / maxVal;
}
fftCurr[i] = -scale * (float)Math.log10(fftReal[i]*fftReal[i] + fftImag[i]*fftImag[i]);
fftSmooth[i] = smoothing * fftSmooth[i] + ((1 - smoothing) * fftCurr[i]);
stroke(i,100,100);
line( i, height/2, i, height/2 - (mousePressed ? fftSmooth[i] : fftCurr[i]));
}
text("smoothing: " + (int)(smoothing*100)+"nwindow:"+wlabel[windex]+"nscale:"+scale,10,10);
}
void keyPressed(){
float inc = 0.01;
if(keyCode == UP && smoothing < 1-inc) smoothing += inc;
if(keyCode == DOWN && smoothing > inc) smoothing -= inc;
if(key == 'W' && windex < window.length-1) windex++;
if(key == 'w' && windex > 0) windex--;
if(key == 'w' || key == 'W') fft.window(window[windex]);
if(keyCode == LEFT && scale > 1) scale--;
if(keyCode == RIGHT) scale++;
}
produit:
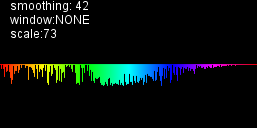
dans la boucle de tirage je tire du centre puisque l'échelle est maintenant négative. Si je mets les valeurs à l'échelle, le résultat devient aléatoire.
UPDATE6
import ddf.minim.analysis.*;
import ddf.minim.*;
Minim minim;
AudioInput in;
FFT fft;
float smoothing = 0;
float[] fftReal;
float[] fftImag;
float[] fftSmooth;
float[] fftPrev;
float[] fftCurr;
int specSize;
WindowFunction[] window = {FFT.NONE,FFT.HAMMING,FFT.HANN,FFT.COSINE,FFT.TRIANGULAR,FFT.BARTLETT,FFT.BARTLETTHANN,FFT.LANCZOS,FFT.BLACKMAN,FFT.GAUSS};
String[] wlabel = {"NONE","HAMMING","HANN","COSINE","TRIANGULAR","BARTLETT","BARTLETTHANN","LANCZOS","BLACKMAN","GAUSS"};
int windex = 0;
int scale = 10;
void setup(){
minim = new Minim(this);
in = minim.getLineIn(Minim.STEREO, 512);
fft = new FFT(in.bufferSize(), in.sampleRate());
fft.window(window[windex]);
specSize = fft.specSize();
fftSmooth = new float[specSize];
fftPrev = new float[specSize];
fftCurr = new float[specSize];
size(specSize, specSize/2);
colorMode(HSB,specSize,100,100);
}
void draw(){
background(0);
stroke(255);
fft.forward( in.mix);
fftReal = fft.getSpectrumReal();
fftImag = fft.getSpectrumImaginary();
for(int i = 0; i < specSize; i++)
{
fftCurr[i] = scale * (float)Math.log10(fftReal[i]*fftReal[i] + fftImag[i]*fftImag[i]);
fftSmooth[i] = smoothing * fftSmooth[i] + ((1 - smoothing) * fftCurr[i]);
stroke(i,100,100);
line( i, height/2, i, height/2 - (mousePressed ? fftSmooth[i] : fftCurr[i]));
}
text("smoothing: " + (int)(smoothing*100)+"nwindow:"+wlabel[windex]+"nscale:"+scale,10,10);
}
void keyPressed(){
float inc = 0.01;
if(keyCode == UP && smoothing < 1-inc) smoothing += inc;
if(keyCode == DOWN && smoothing > inc) smoothing -= inc;
if(key == 'W' && windex < window.length-1) windex++;
if(key == 'w' && windex > 0) windex--;
if(key == 'w' || key == 'W') fft.window(window[windex]);
if(keyCode == LEFT && scale > 1) scale--;
if(keyCode == RIGHT) scale++;
if(key == 's') saveFrame("fftmod.png");
}
Cela se sent si proche:
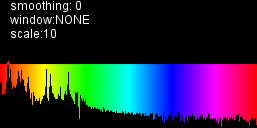
cela semble beaucoup mieux que la version précédente, mais quelques valeurs sur le côté inférieur / gauche du spectre l'air un peu hors et la forme semble changer très vite. (les valeurs lissées indiquent des zéros)
2 réponses
Je ne sais pas exactement quel type de lissage vous voulez faire, mais je vais essayer de fournir quelques informations qui pourraient vous aider.
mise à L'échelle des résultats FFT pour affichage
généralement, quand vous prenez la Transformée de Fourier et vous souhaitez afficher un graphique de l', vous avez besoin (comme vous le mentionnez) de l'échelle logarithmique. C'est parce que l'ampleur des valeurs variera sur une gamme énorme - de nombreux ordres de grandeur - et en comprimant cette dans le petit espace observable sur un graphique permet d'entraîner les principaux sommets à éclipser le reste de l'information.
pour réaliser cette mise à l'échelle, nous convertissons les valeurs en décibels. Il est important de noter que decibels est une échelle et non une unité - il représente un rapport entre deux nombres: généralement une valeur mesurée et une référence. La formule générale pour les décibels est
x_dB = 10 * log10((x ^ 2) / (ref ^ 2))
où log10 is logarithme to base 10,^ est le pouvoir l'opérateur, et x_ref est la valeur de référence que vous avez choisie. Puisque les valeurs FFT d'un fichier audio n'ont pas (habituellement) d'unités significatives,x_ref est généralement choisi pour être simplement 1 pour cette application. En outre, depuis le x est complexe, vous devez prendre la valeur absolue. Ainsi, la formule sera
x_dB = 10 * log10(abs(x) ^ 2)
il y a une petite optimisation (numérique et de vitesse) possible ici, puisque vous êtes en train de corriger le résultat d'une racine carrée:
x_dB = 10 * log10(real(x) ^ 2 + imag(x) ^ 2)
perception pondération
mise à L'échelle des mesures du domaine de fréquence est généralement fait lors de la mesure de la pression et de la puissance du son: un type de mesure spécifique est choisi pour l'application donnée (Je ne vais pas entrer dans les types ici), et un enregistrement du son est fait en fonction de ce type de mesure. Le résultat est FFT et ensuite multiplié par une pondération donnée à chaque fréquence en fonction de ce que le résultat sera utilisé et du type de son enregistré. Il y a deux pondérations dans usage courant: A, et C. C n'est généralement utilisé que pour les sons de très grande amplitude.
notez que ce type de pondération n'est pas vraiment nécessaire si vous voulez simplement afficher un joli graphique: il est utilisé pour s'assurer que tout le monde dans le monde peut faire des mesures (et de l'équipement de mesure) qui suivent la même norme. Si vous décidez d'inclure cela, il doit être réalisée comme une multiplication avant conversion en décibels (ou en plus de la décibels valeur de la pondération - qui est mathématiquement équivalente).
Info sur la pondération A est wikipédia.
fenêtrage
le fenêtrage est effectué principalement pour réduire l'effet du phénomène Gibbs. On ne peut jamais s'en débarrasser complètement, mais le fenêtrage aide. Malheureusement, elle a d'autres effets: les pics pointus sont élargis et des" lobes secondaires " sont introduits; il y a toujours un compromis entre la netteté des pics et hauteur du lobe latéral. Je ne vais pas entrer dans tous les détails à moins que vous ne le demandiez expressément; il y a une explication assez longue du fenêtrage!--58-->dans ce livre électronique gratuit.
lissage du domaine temporel des bacs de fréquence individuels
pour ce qui est de faire la ligne dans chaque bin de fréquence décroître lentement, voici une idée simple qui pourrait faire l'affaire: dans chaque bin de fréquence, appliquer une moyenne exponentielle simple mobile. Dites que vos résultats sont stockés dans X[k], où k est l'indice de fréquence. Laissez votre valeur d'affichage Y[k] tels que
Y[k] = alpha * Y_(t-1)[k] + (1 - alpha) * X[k]
où 0 < alpha < 1 est votre facteur de lissage, et Y_(t-1)[k] est la valeur de Y[k]dernière étape (t-1). Il s'agit en fait d'un filtre IIR (infinite impulse response) simple passe-bas (infinite impulse response), et nous espérons devrait faire essentiellement ce que vous voulez (peut-être avec un peu de retouche). Plus l'alpha est proche de zéro, plus les nouvelles observations sont rapides (entrée X[k]) affectera le résultat. Le plus c'est l'un, plus lentement, le résultat de la décomposition, mais l'entrée sera également affecter le résultat plus lentement, de sorte qu'il peut paraître "lente". Vous pouvez ajouter un conditionnel autour d'elle pour prendre la nouvelle valeur immédiatement si elle est supérieure à la valeur actuelle.
Notez que, encore une fois, cela devrait être effectué avant la conversion en décibels.
(edit) après avoir regardé le code que vous avez posté un peu plus clairement, cela apparaît la méthode utilisée dans l'exemple, vous êtes à essayer de les reproduire. Votre tentative initiale était proche, mais notez que le premier terme est le coefficient de lissage multiplié par le dernier valeur d'affichage, pas le courant d'entrée.
(edit 2) votre troisième mise à jour est, encore une fois, proche, mais il y a une légère erreur de traduction de la formule dans les lignes suivantes
fftSmooth[i] = smoothing * fftPrev[i] + ((1 - smoothing) * fftCurr[i]);
fftPrev[i] = fftCurr[i];//
au lieu de la valeur précédente des coefficients FFT avant lissage, vous voulez prendre la valeur après lissage. (notez que cela signifie que vous n'avez pas réellement besoin d'un autre tableau pour stocker la valeur précédente)
fftSmooth[i] = smoothing * fftSmooth[i] + ((1 - smoothing) * fftCurr[i]);
Si smoothing == 0, cette ligne devrait avoir peu d'effet autre que de multiplier le résultat par un scalaire.
normalisation dans le calcul de la valeur absolue
en regardant de plus près la façon dont ils calculent la valeur absolue, ils ont une normalisation là-dedans, de sorte que celui des deux complexes les valeurs est le maximum, devient 1, et l'autre est graduée en conséquence. Cela signifie que vous obtiendrez toujours une valeur absolue entre 0 et 1, et est probablement leur alternative à la conversion de décibel. Vraiment, ce n'est pas tout à fait ce que la documentation de abs fonction suggère, ce qui est un peu ennuyeux... mais de toute façon, si vous répliquez ceci, cela garantira que vos valeurs sont toujours dans une plage raisonnable.
pour faire cela simplement dans votre code, vous pourriez faire quelque chose comme
float maxVal = Math.max(Math.abs(fftReal[i]), Math.abs(fftImag[i]));
if (maxVal != 0.0f) { // prevent divide-by-zero
// Normalize
fftReal[i] = fftReal[i] / maxVal;
fftImag[i] = fftImag[i] / maxVal;
}
fftCurr[i] = scale * (float)Math.log10(fftReal[i]*fftReal[i] + fftImag[i]*fftImag[i]);
// ...
Mettre tous ensemble: un peu de code
ayant joué avec pendant un certain temps dans le traitement 2.1, j'ai une solution dont je pense que vous serez heureux:
import ddf.minim.analysis.*;
import ddf.minim.*;
Minim minim;
//AudioInput in;
AudioPlayer in;
FFT fft;
float smoothing = 0.60;
final boolean useDB = true;
final int minBandwidthPerOctave = 200;
final int bandsPerOctave = 10;
float[] fftSmooth;
int avgSize;
float minVal = 0.0;
float maxVal = 0.0;
boolean firstMinDone = false;
void setup(){
minim = new Minim(this);
//in = minim.getLineIn(Minim.STEREO, 512);
in = minim.loadFile("C:\path\to\some\audio\file.ext", 2048);
in.loop();
fft = new FFT(in.bufferSize(), in.sampleRate());
// Use logarithmically-spaced averaging
fft.logAverages(minBandwidthPerOctave, bandsPerOctave);
avgSize = fft.avgSize();
fftSmooth = new float[avgSize];
int myWidth = 500;
int myHeight = 250;
size(myWidth, myHeight);
colorMode(HSB,avgSize,100,100);
}
float dB(float x) {
if (x == 0) {
return 0;
}
else {
return 10 * (float)Math.log10(x);
}
}
void draw(){
background(0);
stroke(255);
fft.forward( in.mix);
final int weight = width / avgSize;
final float maxHeight = (height / 2) * 0.75;
for (int i = 0; i < avgSize; i++) {
// Get spectrum value (using dB conversion or not, as desired)
float fftCurr;
if (useDB) {
fftCurr = dB(fft.getAvg(i));
}
else {
fftCurr = fft.getAvg(i);
}
// Smooth using exponential moving average
fftSmooth[i] = (smoothing) * fftSmooth[i] + ((1 - smoothing) * fftCurr);
// Find max and min values ever displayed across whole spectrum
if (fftSmooth[i] > maxVal) {
maxVal = fftSmooth[i];
}
if (!firstMinDone || (fftSmooth[i] < minVal)) {
minVal = fftSmooth[i];
}
}
// Calculate the total range of smoothed spectrum; this will be used to scale all values to range 0...1
final float range = maxVal - minVal;
final float scaleFactor = range + 0.00001; // avoid div. by zero
for(int i = 0; i < avgSize; i++)
{
stroke(i,100,100);
strokeWeight(weight);
// Y-coord of display line; fftSmooth is scaled to range 0...1; this is then multiplied by maxHeight
// to make it within display port range
float fftSmoothDisplay = maxHeight * ((fftSmooth[i] - minVal) / scaleFactor);
// X-coord of display line
float x = i * weight;
line(x, height / 2, x, height / 2 - fftSmoothDisplay);
}
text("smoothing: " + (int)(smoothing*100)+"\n",10,10);
}
void keyPressed(){
float inc = 0.01;
if(keyCode == UP && smoothing < 1-inc) smoothing += inc;
if(keyCode == DOWN && smoothing > inc) smoothing -= inc;
}
ce qui précède utilise une approche légèrement différente-la moyenne du spectre dans une série de bacs qui est plus petite que la taille totale du spectre - qui produit un résultat plus proche de WMP's que votre original.
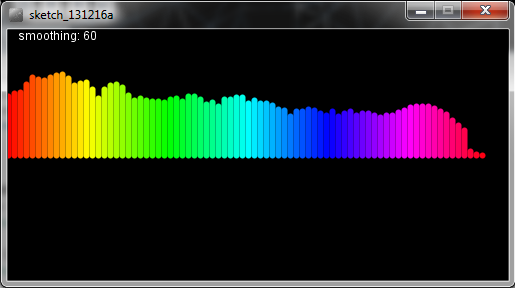
Amélioration: Maintenant, avec Une pondération
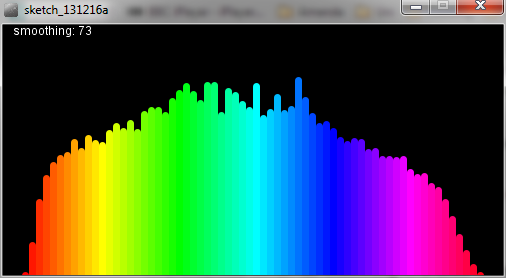
j'ai une version mise à jour du code qui applique la pondération A dans chaque bande de fréquences (mais seulement lorsque le mode dB est activé, parce que le tableau que j'avais était en dB :). Transformer Une pondération pour un résultat plus proche de WMP, ou dans un plus proche de VLC.
Il y a aussi quelques modifications mineures à la façon dont il est affiché: il est désormais centré sur l'écran et il va s'afficher uniquement jusqu'à une fréquence centrale maximale de bande.
voici le code-enjoy!
import ddf.minim.analysis.*;
import ddf.minim.*;
Minim minim;
//AudioInput in;
AudioPlayer in;
FFT fft;
float smoothing = 0.73;
final boolean useDB = true;
final boolean useAWeighting = true; // only used in dB mode, because the table I found was in dB
final boolean resetBoundsAtEachStep = false;
final float maxViewportUsage = 0.85;
final int minBandwidthPerOctave = 200;
final int bandsPerOctave = 10;
final float maxCentreFrequency = 18000;
float[] fftSmooth;
int avgSize;
float minVal = 0.0;
float maxVal = 0.0;
boolean firstMinDone = false;
final float[] aWeightFrequency = {
10, 12.5, 16, 20,
25, 31.5, 40, 50,
63, 80, 100, 125,
160, 200, 250, 315,
400, 500, 630, 800,
1000, 1250, 1600, 2000,
2500, 3150, 4000, 5000,
6300, 8000, 10000, 12500,
16000, 20000
};
final float[] aWeightDecibels = {
-70.4, -63.4, -56.7, -50.5,
-44.7, -39.4, -34.6, -30.2,
-26.2, -22.5, -19.1, -16.1,
-13.4, -10.9, -8.6, -6.6,
-4.8, -3.2, -1.9, -0.8,
0.0, 0.6, 1.0, 1.2,
1.3, 1.2, 1.0, 0.5,
-0.1, -1.1, -2.5, -4.3,
-6.6, -9.3
};
float[] aWeightDBAtBandCentreFreqs;
void setup(){
minim = new Minim(this);
//in = minim.getLineIn(Minim.STEREO, 512);
in = minim.loadFile("D:\Music\Arthur Brown\The Crazy World Of Arthur Brown\1-09 Fire.mp3", 2048);
in.loop();
fft = new FFT(in.bufferSize(), in.sampleRate());
// Use logarithmically-spaced averaging
fft.logAverages(minBandwidthPerOctave, bandsPerOctave);
aWeightDBAtBandCentreFreqs = calculateAWeightingDBForFFTAverages(fft);
avgSize = fft.avgSize();
// Only use freqs up to maxCentreFrequency - ones above this may have
// values too small that will skew our range calculation for all time
while (fft.getAverageCenterFrequency(avgSize-1) > maxCentreFrequency) {
avgSize--;
}
fftSmooth = new float[avgSize];
int myWidth = 500;
int myHeight = 250;
size(myWidth, myHeight);
colorMode(HSB,avgSize,100,100);
}
float[] calculateAWeightingDBForFFTAverages(FFT fft) {
float[] result = new float[fft.avgSize()];
for (int i = 0; i < result.length; i++) {
result[i] = calculateAWeightingDBAtFrequency(fft.getAverageCenterFrequency(i));
}
return result;
}
float calculateAWeightingDBAtFrequency(float frequency) {
return linterp(aWeightFrequency, aWeightDecibels, frequency);
}
float dB(float x) {
if (x == 0) {
return 0;
}
else {
return 10 * (float)Math.log10(x);
}
}
float linterp(float[] x, float[] y, float xx) {
assert(x.length > 1);
assert(x.length == y.length);
float result = 0.0;
boolean found = false;
if (x[0] > xx) {
result = y[0];
found = true;
}
if (!found) {
for (int i = 1; i < x.length; i++) {
if (x[i] > xx) {
result = y[i-1] + ((xx - x[i-1]) / (x[i] - x[i-1])) * (y[i] - y[i-1]);
found = true;
break;
}
}
}
if (!found) {
result = y[y.length-1];
}
return result;
}
void draw(){
background(0);
stroke(255);
fft.forward( in.mix);
final int weight = width / avgSize;
final float maxHeight = height * maxViewportUsage;
final float xOffset = weight / 2 + (width - avgSize * weight) / 2;
if (resetBoundsAtEachStep) {
minVal = 0.0;
maxVal = 0.0;
firstMinDone = false;
}
for (int i = 0; i < avgSize; i++) {
// Get spectrum value (using dB conversion or not, as desired)
float fftCurr;
if (useDB) {
fftCurr = dB(fft.getAvg(i));
if (useAWeighting) {
fftCurr += aWeightDBAtBandCentreFreqs[i];
}
}
else {
fftCurr = fft.getAvg(i);
}
// Smooth using exponential moving average
fftSmooth[i] = (smoothing) * fftSmooth[i] + ((1 - smoothing) * fftCurr);
// Find max and min values ever displayed across whole spectrum
if (fftSmooth[i] > maxVal) {
maxVal = fftSmooth[i];
}
if (!firstMinDone || (fftSmooth[i] < minVal)) {
minVal = fftSmooth[i];
}
}
// Calculate the total range of smoothed spectrum; this will be used to scale all values to range 0...1
final float range = maxVal - minVal;
final float scaleFactor = range + 0.00001; // avoid div. by zero
for(int i = 0; i < avgSize; i++)
{
stroke(i,100,100);
strokeWeight(weight);
// Y-coord of display line; fftSmooth is scaled to range 0...1; this is then multiplied by maxHeight
// to make it within display port range
float fftSmoothDisplay = maxHeight * ((fftSmooth[i] - minVal) / scaleFactor);
// Artificially impose a minimum of zero (this is mathematically bogus, but whatever)
fftSmoothDisplay = max(0.0, fftSmoothDisplay);
// X-coord of display line
float x = xOffset + i * weight;
line(x, height, x, height - fftSmoothDisplay);
}
text("smoothing: " + (int)(smoothing*100)+"\n",10,10);
}
void keyPressed(){
float inc = 0.01;
if(keyCode == UP && smoothing < 1-inc) smoothing += inc;
if(keyCode == DOWN && smoothing > inc) smoothing -= inc;
}
dans votre boucle: vous devez ajouter un calcul logarithmique pour une échelle lg:
stroke(i,100,50);
line( i, height, i, height - fftSmooth[i]*8 );
stroke(i,100,100);
line( i, height, i, height - band*8 );
devrait être changée en:
int l = map(log(map(i ,0 ,specSize,0,100),0,2,0,width). // an estimation, may have to calibrate
stroke(i,100,50);
line( l, height, l, height - fftSmooth[i]*8 );
stroke(i,100,100);
line( l, height, l, height - band*8 );