Comment dessiner une Perspective-grille correcte en 2D
j'ai une application qui définit un rectangle du monde réel sur une image/Photographie, bien sûr en 2D il ne peut pas être un rectangle parce que vous le regardez d'un angle.
le problème est, disons que le rectangle doit avoir des lignes de grille dessinées dessus, par exemple si elle est de 3x5 donc je dois dessiner 2 lignes de côté 1 à côté 3, et 4 lignes de côté 2 à côté 4.
à partir de Maintenant je divise chaque ligne en parties équidistantes, pour obtenir le début et la fin de toutes les lignes de la grille. Cependant plus l'angle du rectangle est sur, plus "incorrect" ces lignes deviennent, comme les lignes horizontales plus loin de vous devraient être plus près ensemble.
est-ce que quelqu'un connaît le nom de l'algorithme que je devrais chercher?
Oui je sais que vous pouvez faire cela en 3D, mais je suis limité à 2D pour cette application particulière.
11 réponses
Voici la solution: http://freespace.virgin.net/hugo.elias/graphics/x_persp.htm
l'idée de base est que vous pouvez trouver la perspective correcte" centre " de votre rectangle en reliant les coins diagonalement. L'intersection des deux lignes résultantes est votre centre correct de perspective. De là, vous subdivisez votre rectangle en quatre petits rectangles, et vous répétez le processus. Le nombre de fois dépend de la précision que vous souhaitez il. Vous pouvez subdiviser à juste au-dessous de la taille d'un pixel pour la perspective effectivement parfaite.
alors dans vos sous-rectangles vous appliquez juste vos triangles "texturés" standard, ou rectangles ou n'importe quoi.
vous pouvez effectuer cet algorithme sans aller à la difficulté complexe de construire un monde 3d 'réel'. il est également bon pour si vous do avoir un monde réel 3D modélisé, mais vos textriangles ne sont pas perspective corrigé dans le matériel, ou vous avez besoin d'un moyen performant pour obtenir des plans corrects en perspective Sans par pixel Rendu tromperie.
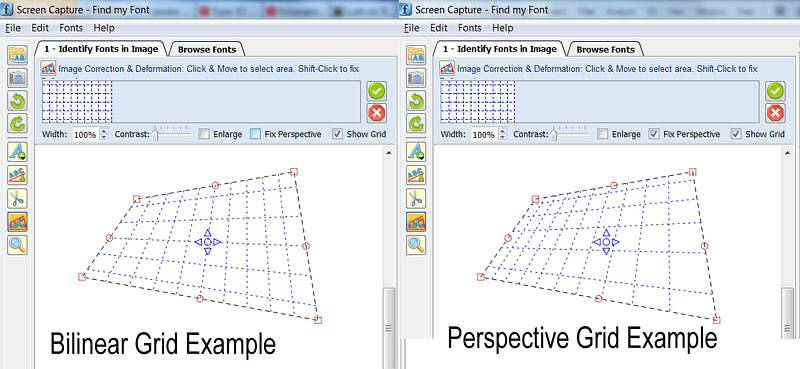Image: Exemple de transformation Bilinéaire et Perspective (Note: la hauteur des lignes de quadrillage horizontales du haut et du bas est en fait la moitié de la hauteur des lignes de repos, sur les deux dessins)
========================================
je sais que c'est une vieille question, mais j'ai une solution générique donc j'ai décidé de la publier sautillant il sera utile aux futurs lecteurs. Le code ci-dessous peut dessiner une grille de perspective arbitraire sans avoir besoin de calculs répétitifs.
je commence en fait avec un problème similaire: dessiner une grille de perspective 2D et puis transformer l'image de soulignement pour restaurer la perspective.
j'ai commencé à lire ici: http://www.imagemagick.org/Usage/distorts/#bilinear_forward
et puis ici (la bibliothèque Leptonica): http://www.leptonica.com/affine.html
où j'ai trouvé ceci:
quand vous regardez un objet dans un plan à partir d'une direction arbitraire à une distance limitée, vous obtenez une distorsion "clé de voûte" supplémentaire dans le image. C'est une transformation projective, qui conserve les lignes droites droit mais ne préserve pas les angles entre les lignes. Cette déformation ne peut être décrit par une transformation affine linéaire, et en fait diffère par les Termes dépendant de x et de y dans le dénominateur.
la transformation n'est pas linéaire, comme beaucoup de gens l'ont déjà souligné dans ce fil. Il s'agit de résoudre un système linéaire de 8 équations (une fois) pour calculer les 8 coefficients requis, puis vous pouvez les utiliser pour transformer autant de points que vous voulez.
pour éviter d'inclure toute bibliothèque Leptonica dans mon projet, j'ai pris quelques morceaux de code, j'ai enlevé tous les types de données et macros Leptonica Spéciaux, j'ai corrigé quelques fuites de mémoire et je l'ai converti en un Classe C++ (principalement pour des raisons d'encapsulation) qui ne fait qu'une chose: Il établit une correspondance entre les coordonnées a (Qt) qpointtf float (x,y) et la coordonnée de Perspective correspondante.
si vous voulez adapter le code à une autre bibliothèque C++, la seule chose à redéfinir/substituer est la classe de coordonnées Qpointtf.
j'espère que d'autres lecteurs le trouveront utile. Le code ci-dessous est divisé en 3 parties:
A. exemple d'utilisation de la genImageProjective classe C++ pour dessiner un point de vue 2D de la Grille
B. genImageProjective.h fichier
c. genImageProjective.fichier cpp
//============================================================
// C++ Code Example on how to use the
// genImageProjective class to draw a perspective 2D Grid
//============================================================
#include "genImageProjective.h"
// Input: 4 Perspective-Tranformed points:
// perspPoints[0] = top-left
// perspPoints[1] = top-right
// perspPoints[2] = bottom-right
// perspPoints[3] = bottom-left
void drawGrid(QPointF *perspPoints)
{
(...)
// Setup a non-transformed area rectangle
// I use a simple square rectangle here because in this case we are not interested in the source-rectangle,
// (we want to just draw a grid on the perspPoints[] area)
// but you can use any arbitrary rectangle to perform a real mapping to the perspPoints[] area
QPointF topLeft = QPointF(0,0);
QPointF topRight = QPointF(1000,0);
QPointF bottomRight = QPointF(1000,1000);
QPointF bottomLeft = QPointF(0,1000);
float width = topRight.x() - topLeft.x();
float height = bottomLeft.y() - topLeft.y();
// Setup Projective trasform object
genImageProjective imageProjective;
imageProjective.sourceArea[0] = topLeft;
imageProjective.sourceArea[1] = topRight;
imageProjective.sourceArea[2] = bottomRight;
imageProjective.sourceArea[3] = bottomLeft;
imageProjective.destArea[0] = perspPoints[0];
imageProjective.destArea[1] = perspPoints[1];
imageProjective.destArea[2] = perspPoints[2];
imageProjective.destArea[3] = perspPoints[3];
// Compute projective transform coefficients
if (imageProjective.computeCoeefficients() != 0)
return; // This can actually fail if any 3 points of Source or Dest are colinear
// Initialize Grid parameters (without transform)
float gridFirstLine = 0.1f; // The normalized position of first Grid Line (0.0 to 1.0)
float gridStep = 0.1f; // The normalized Grd size (=distance between grid lines: 0.0 to 1.0)
// Draw Horizonal Grid lines
QPointF lineStart, lineEnd, tempPnt;
for (float pos = gridFirstLine; pos <= 1.0f; pos += gridStep)
{
// Compute Grid Line Start
tempPnt = QPointF(topLeft.x(), topLeft.y() + pos*width);
imageProjective.mapSourceToDestPoint(tempPnt, lineStart);
// Compute Grid Line End
tempPnt = QPointF(topRight.x(), topLeft.y() + pos*width);
imageProjective.mapSourceToDestPoint(tempPnt, lineEnd);
// Draw Horizontal Line (use your prefered method to draw the line)
(...)
}
// Draw Vertical Grid lines
for (float pos = gridFirstLine; pos <= 1.0f; pos += gridStep)
{
// Compute Grid Line Start
tempPnt = QPointF(topLeft.x() + pos*height, topLeft.y());
imageProjective.mapSourceToDestPoint(tempPnt, lineStart);
// Compute Grid Line End
tempPnt = QPointF(topLeft.x() + pos*height, bottomLeft.y());
imageProjective.mapSourceToDestPoint(tempPnt, lineEnd);
// Draw Vertical Line (use your prefered method to draw the line)
(...)
}
(...)
}
==========================================
//========================================
//C++ Header File: genImageProjective.h
//========================================
#ifndef GENIMAGE_H
#define GENIMAGE_H
#include <QPointF>
// Class to transform an Image Point using Perspective transformation
class genImageProjective
{
public:
genImageProjective();
int computeCoeefficients(void);
int mapSourceToDestPoint(QPointF& sourcePoint, QPointF& destPoint);
public:
QPointF sourceArea[4]; // Source Image area limits (Rectangular)
QPointF destArea[4]; // Destination Image area limits (Perspectivelly Transformed)
private:
static int gaussjordan(float **a, float *b, int n);
bool coefficientsComputed;
float vc[8]; // Vector of Transform Coefficients
};
#endif // GENIMAGE_H
//========================================
//========================================
//C++ CPP File: genImageProjective.cpp
//========================================
#include <math.h>
#include "genImageProjective.h"
// ----------------------------------------------------
// class genImageProjective
// ----------------------------------------------------
genImageProjective::genImageProjective()
{
sourceArea[0] = sourceArea[1] = sourceArea[2] = sourceArea[3] = QPointF(0,0);
destArea[0] = destArea[1] = destArea[2] = destArea[3] = QPointF(0,0);
coefficientsComputed = false;
}
// --------------------------------------------------------------
// Compute projective transform coeeeficients
// RetValue: 0: Success, !=0: Error
/*-------------------------------------------------------------*
* Projective coordinate transformation *
*-------------------------------------------------------------*/
/*!
* computeCoeefficients()
*
* Input: this->sourceArea[4]: (source 4 points; unprimed)
* this->destArea[4]: (transformed 4 points; primed)
* this->vc (computed vector of transform coefficients)
* Return: 0 if OK; <0 on error
*
* We have a set of 8 equations, describing the projective
* transformation that takes 4 points (sourceArea) into 4 other
* points (destArea). These equations are:
*
* x1' = (c[0]*x1 + c[1]*y1 + c[2]) / (c[6]*x1 + c[7]*y1 + 1)
* y1' = (c[3]*x1 + c[4]*y1 + c[5]) / (c[6]*x1 + c[7]*y1 + 1)
* x2' = (c[0]*x2 + c[1]*y2 + c[2]) / (c[6]*x2 + c[7]*y2 + 1)
* y2' = (c[3]*x2 + c[4]*y2 + c[5]) / (c[6]*x2 + c[7]*y2 + 1)
* x3' = (c[0]*x3 + c[1]*y3 + c[2]) / (c[6]*x3 + c[7]*y3 + 1)
* y3' = (c[3]*x3 + c[4]*y3 + c[5]) / (c[6]*x3 + c[7]*y3 + 1)
* x4' = (c[0]*x4 + c[1]*y4 + c[2]) / (c[6]*x4 + c[7]*y4 + 1)
* y4' = (c[3]*x4 + c[4]*y4 + c[5]) / (c[6]*x4 + c[7]*y4 + 1)
*
* Multiplying both sides of each eqn by the denominator, we get
*
* AC = B
*
* where B and C are column vectors
*
* B = [ x1' y1' x2' y2' x3' y3' x4' y4' ]
* C = [ c[0] c[1] c[2] c[3] c[4] c[5] c[6] c[7] ]
*
* and A is the 8x8 matrix
*
* x1 y1 1 0 0 0 -x1*x1' -y1*x1'
* 0 0 0 x1 y1 1 -x1*y1' -y1*y1'
* x2 y2 1 0 0 0 -x2*x2' -y2*x2'
* 0 0 0 x2 y2 1 -x2*y2' -y2*y2'
* x3 y3 1 0 0 0 -x3*x3' -y3*x3'
* 0 0 0 x3 y3 1 -x3*y3' -y3*y3'
* x4 y4 1 0 0 0 -x4*x4' -y4*x4'
* 0 0 0 x4 y4 1 -x4*y4' -y4*y4'
*
* These eight equations are solved here for the coefficients C.
*
* These eight coefficients can then be used to find the mapping
* (x,y) --> (x',y'):
*
* x' = (c[0]x + c[1]y + c[2]) / (c[6]x + c[7]y + 1)
* y' = (c[3]x + c[4]y + c[5]) / (c[6]x + c[7]y + 1)
*
*/
int genImageProjective::computeCoeefficients(void)
{
int retValue = 0;
int i;
float *a[8]; /* 8x8 matrix A */
float *b = this->vc; /* rhs vector of primed coords X'; coeffs returned in vc[] */
b[0] = destArea[0].x();
b[1] = destArea[0].y();
b[2] = destArea[1].x();
b[3] = destArea[1].y();
b[4] = destArea[2].x();
b[5] = destArea[2].y();
b[6] = destArea[3].x();
b[7] = destArea[3].y();
for (i = 0; i < 8; i++)
a[i] = NULL;
for (i = 0; i < 8; i++)
{
if ((a[i] = (float *)calloc(8, sizeof(float))) == NULL)
{
retValue = -100; // ERROR_INT("a[i] not made", procName, 1);
goto Terminate;
}
}
a[0][0] = sourceArea[0].x();
a[0][1] = sourceArea[0].y();
a[0][2] = 1.;
a[0][6] = -sourceArea[0].x() * b[0];
a[0][7] = -sourceArea[0].y() * b[0];
a[1][3] = sourceArea[0].x();
a[1][4] = sourceArea[0].y();
a[1][5] = 1;
a[1][6] = -sourceArea[0].x() * b[1];
a[1][7] = -sourceArea[0].y() * b[1];
a[2][0] = sourceArea[1].x();
a[2][1] = sourceArea[1].y();
a[2][2] = 1.;
a[2][6] = -sourceArea[1].x() * b[2];
a[2][7] = -sourceArea[1].y() * b[2];
a[3][3] = sourceArea[1].x();
a[3][4] = sourceArea[1].y();
a[3][5] = 1;
a[3][6] = -sourceArea[1].x() * b[3];
a[3][7] = -sourceArea[1].y() * b[3];
a[4][0] = sourceArea[2].x();
a[4][1] = sourceArea[2].y();
a[4][2] = 1.;
a[4][6] = -sourceArea[2].x() * b[4];
a[4][7] = -sourceArea[2].y() * b[4];
a[5][3] = sourceArea[2].x();
a[5][4] = sourceArea[2].y();
a[5][5] = 1;
a[5][6] = -sourceArea[2].x() * b[5];
a[5][7] = -sourceArea[2].y() * b[5];
a[6][0] = sourceArea[3].x();
a[6][1] = sourceArea[3].y();
a[6][2] = 1.;
a[6][6] = -sourceArea[3].x() * b[6];
a[6][7] = -sourceArea[3].y() * b[6];
a[7][3] = sourceArea[3].x();
a[7][4] = sourceArea[3].y();
a[7][5] = 1;
a[7][6] = -sourceArea[3].x() * b[7];
a[7][7] = -sourceArea[3].y() * b[7];
retValue = gaussjordan(a, b, 8);
Terminate:
// Clean up
for (i = 0; i < 8; i++)
{
if (a[i])
free(a[i]);
}
this->coefficientsComputed = (retValue == 0);
return retValue;
}
/*-------------------------------------------------------------*
* Gauss-jordan linear equation solver *
*-------------------------------------------------------------*/
/*
* gaussjordan()
*
* Input: a (n x n matrix)
* b (rhs column vector)
* n (dimension)
* Return: 0 if ok, 1 on error
*
* Note side effects:
* (1) the matrix a is transformed to its inverse
* (2) the vector b is transformed to the solution X to the
* linear equation AX = B
*
* Adapted from "Numerical Recipes in C, Second Edition", 1992
* pp. 36-41 (gauss-jordan elimination)
*/
#define SWAP(a,b) {temp = (a); (a) = (b); (b) = temp;}
int genImageProjective::gaussjordan(float **a, float *b, int n)
{
int retValue = 0;
int i, icol=0, irow=0, j, k, l, ll;
int *indexc = NULL, *indexr = NULL, *ipiv = NULL;
float big, dum, pivinv, temp;
if (!a)
{
retValue = -1; // ERROR_INT("a not defined", procName, 1);
goto Terminate;
}
if (!b)
{
retValue = -2; // ERROR_INT("b not defined", procName, 1);
goto Terminate;
}
if ((indexc = (int *)calloc(n, sizeof(int))) == NULL)
{
retValue = -3; // ERROR_INT("indexc not made", procName, 1);
goto Terminate;
}
if ((indexr = (int *)calloc(n, sizeof(int))) == NULL)
{
retValue = -4; // ERROR_INT("indexr not made", procName, 1);
goto Terminate;
}
if ((ipiv = (int *)calloc(n, sizeof(int))) == NULL)
{
retValue = -5; // ERROR_INT("ipiv not made", procName, 1);
goto Terminate;
}
for (i = 0; i < n; i++)
{
big = 0.0;
for (j = 0; j < n; j++)
{
if (ipiv[j] != 1)
{
for (k = 0; k < n; k++)
{
if (ipiv[k] == 0)
{
if (fabs(a[j][k]) >= big)
{
big = fabs(a[j][k]);
irow = j;
icol = k;
}
}
else if (ipiv[k] > 1)
{
retValue = -6; // ERROR_INT("singular matrix", procName, 1);
goto Terminate;
}
}
}
}
++(ipiv[icol]);
if (irow != icol)
{
for (l = 0; l < n; l++)
SWAP(a[irow][l], a[icol][l]);
SWAP(b[irow], b[icol]);
}
indexr[i] = irow;
indexc[i] = icol;
if (a[icol][icol] == 0.0)
{
retValue = -7; // ERROR_INT("singular matrix", procName, 1);
goto Terminate;
}
pivinv = 1.0 / a[icol][icol];
a[icol][icol] = 1.0;
for (l = 0; l < n; l++)
a[icol][l] *= pivinv;
b[icol] *= pivinv;
for (ll = 0; ll < n; ll++)
{
if (ll != icol)
{
dum = a[ll][icol];
a[ll][icol] = 0.0;
for (l = 0; l < n; l++)
a[ll][l] -= a[icol][l] * dum;
b[ll] -= b[icol] * dum;
}
}
}
for (l = n - 1; l >= 0; l--)
{
if (indexr[l] != indexc[l])
{
for (k = 0; k < n; k++)
SWAP(a[k][indexr[l]], a[k][indexc[l]]);
}
}
Terminate:
if (indexr)
free(indexr);
if (indexc)
free(indexc);
if (ipiv)
free(ipiv);
return retValue;
}
// --------------------------------------------------------------
// Map a source point to destination using projective transform
// --------------------------------------------------------------
// Params:
// sourcePoint: initial point
// destPoint: transformed point
// RetValue: 0: Success, !=0: Error
// --------------------------------------------------------------
// Notes:
// 1. You must call once computeCoeefficients() to compute
// the this->vc[] vector of 8 coefficients, before you call
// mapSourceToDestPoint().
// 2. If there was an error or the 8 coefficients were not computed,
// a -1 is returned and destPoint is just set to sourcePoint value.
// --------------------------------------------------------------
int genImageProjective::mapSourceToDestPoint(QPointF& sourcePoint, QPointF& destPoint)
{
if (coefficientsComputed)
{
float factor = 1.0f / (vc[6] * sourcePoint.x() + vc[7] * sourcePoint.y() + 1.);
destPoint.setX( factor * (vc[0] * sourcePoint.x() + vc[1] * sourcePoint.y() + vc[2]) );
destPoint.setY( factor * (vc[3] * sourcePoint.x() + vc[4] * sourcePoint.y() + vc[5]) );
return 0;
}
else // There was an error while computing coefficients
{
destPoint = sourcePoint; // just copy the source to destination...
return -1; // ...and return an error
}
}
//========================================
alors que mon google-fu n'a pas réussi à produire une solution mathématique solide de roche, peut-être ce dessin que j'ai trouvé pourrait aider un peu.
http://studiochalkboard.evansville.edu/lp-diminish.html
Je pense qu'il pourrait être en fait assez difficile de trouver les maths correctes sur votre propre, il est probablement une sorte d'expression logarithmique ou de sommation. Espérons que le dessin et les termes de ce lien pourraient fournir quelque chose un peu plus recherchable pour vous.
en utilisant la méthode de subdivision de Breton (qui est liée à la méthode d'extension de Mongo), vous obtiendrez précise arbitraire pouvoir-de-deux divisions. Pour se diviser en deux divisions non-puissance-de-deux en utilisant ces méthodes, vous devrez subdiviser à l'espacement sub-pixel, qui peut être coûteux en calcul.
cependant, je crois que vous pouvez être en mesure d'appliquer une variation de théorème de Haga (qui est utilisé en origami pour diviser un côté en Nths donné un côté divisé en (N-1)th) aux subdivisions en perspective-carrés pour produire des divisions arbitraires à partir de la puissance la plus proche de 2 sans avoir à continuer à subdiviser.
la solution la plus élégante et la plus rapide serait de trouver la matrice d'homographie, qui établit une correspondance entre les coordonnées rectangulaires et les coordonnées photographiques.
avec une bibliothèque de matrices décente, ce ne devrait pas être une tâche difficile, tant que vous connaissez vos maths.
Mots Clés: Collinéation, Homographie, Transformation Linéaire Directe
Cependant, l'algorithme récursif ci-dessus devrait fonctionner, mais probablement pas si vos ressources sont limitées, projectives la géométrie est la seule façon d'aller.
dans le cas particulier quand vous regardez perpendiculairement aux côtés 1 et 3, vous pouvez diviser ces côtés en parties égales. Dessinez ensuite une diagonale et tracez des parallèles au côté 1 à travers chaque intersection de la diagonale et des lignes de division tracées précédemment.
c'est une solution géométrique que j'ai pensé. Je ne sais pas si le 'algorithme' a un nom.
dites que vous voulez commencer par diviser le 'rectangle' en n morceaux avec des lignes verticales en premier.
le but est de placer les points P1..Pn-1 sur la ligne supérieure que nous pouvons utiliser pour tracer des lignes à travers eux aux points où la ligne de gauche et droite se rencontrent ou parallèle à eux quand un tel point n'existe pas.
Si le haut et le bas les lignes sont parallèles les uns aux autres il suffit de placer ces points pour diviser la ligne supérieure entre les coins de façon équidistante.
autre place n Points Q1..Qn sur la ligne de gauche de sorte que theese et le coin supérieur gauche sont équidistant et i < j => Qi est plus proche du coin supérieur gauche que Qj. Afin de cartographier les Q-points à la ligne du haut trouver l'intersection S de la ligne de Qn à travers le coin supérieur droit et le parallèle à la ligne de gauche à travers l'intersection du haut et du bas ligne. Maintenant connectez S avec Q1..Qn-1. L'intersection des nouvelles lignes avec la ligne du haut sont les p-points recherchés.
cela analogique pour les lignes horizontales.
compte tenu d'une rotation autour de l'axe y, surtout si les surfaces de rotation sont planes, la perspective est générée par des gradients verticaux. Ceux-ci se rapprochent progressivement dans la perspective. Au lieu d'utiliser des diagonales pour définir quatre rectangles, qui peuvent fonctionner avec des pouvoirs donnés de deux... définissez deux rectangles, gauche et droite. Ils seront plus hauts que larges, éventuellement, si on continue à diviser la surface en segments verticaux plus étroits. Cela peut accommoder des surfaces qui ne sont pas carrées. Si un la rotation est autour de l'axe des x, puis des gradients horizontaux sont nécessaires.
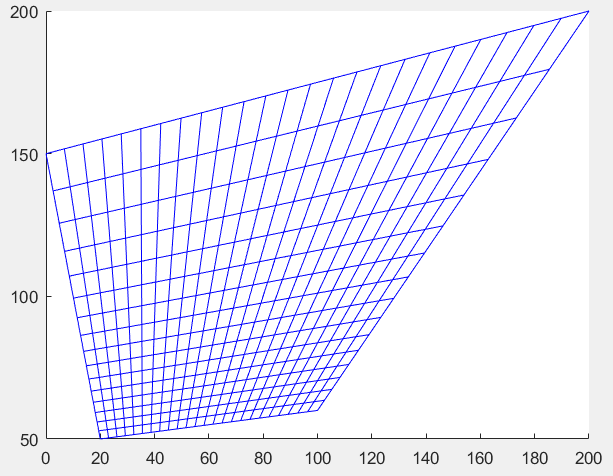
je pense que la réponse choisie n'est pas la meilleure solution disponible. Une meilleure solution consiste à appliquer la transformation de perspective (projective) d'un rectangle à une grille simple comme suit MATLAB script et image show. Vous pouvez implémenter cet algorithme avec C++ et OpenCV.
function drawpersgrid
sz = [ 24, 16 ]; % [x y]
srcpt = [ 0 0; sz(1) 0; 0 sz(2); sz(1) sz(2)];
destpt = [ 20 50; 100 60; 0 150; 200 200;];
% make rectangular grid
[X,Y] = meshgrid(0:sz(1),0:sz(2));
% find projective transform matching corner points
tform = maketform('projective',srcpt,destpt);
% apply the projective transform to the grid
[X1,Y1] = tformfwd(tform,X,Y);
hold on;
%% find grid
for i=1:sz(2)
for j=1:sz(1)
x = [ X1(i,j);X1(i,j+1);X1(i+1,j+1);X1(i+1,j);X1(i,j)];
y = [ Y1(i,j);Y1(i,j+1);Y1(i+1,j+1);Y1(i+1,j);Y1(i,j)];
plot(x,y,'b');
end
end
hold off;
le problème, c'est que c'est la transformation de la 3D en 2D qui vous attire.
ici est un tutoriel sur la façon de faire.
ce que vous devez faire est de le représenter en 3D (monde) puis de le projeter en 2D (écran).
cela vous demandera d'utiliser une matrice de transformation 4D qui fait la projection sur un 4D homogène vers le bas à un vecteur homogène 3D, que vous pouvez ensuite convertir vers le bas à un vecteur d'espace d'écran 2D.
je ne pouvais pas le trouver dans Google, mais une bonne infographie livres les détails.
mots clés sont matrice de projection, projection de transformation, transformation affine, homogène vecteur, le monde, l'espace, l'espace de l'écran, la perspective de la transformation, de transformation 3D
et d'ailleurs, il faut généralement quelques conférences pour expliquer tout cela. Donc, bonne chance.