Comment faire un ajustement de courbe exponentielle et logarithmique en Python? J'ai trouvé seulement un ajustement polynomial
J'ai un ensemble de données et je veux comparer quelle ligne Le décrit le mieux (polynômes d'ordres différents, exponentiels ou logarithmiques).
J'utilise Python et Numpy et pour polynôme côté il y a une fonction polyfit(). Mais je n'ai pas trouvé de telles fonctions pour l'ajustement exponentiel et logarithmique.
Y en a-t-il? Ou comment le résoudre autrement?
4 réponses
Pour le montage de y = Un + B log x, juste la forme y contre (log x).
>>> x = numpy.array([1, 7, 20, 50, 79])
>>> y = numpy.array([10, 19, 30, 35, 51])
>>> numpy.polyfit(numpy.log(x), y, 1)
array([ 8.46295607, 6.61867463])
# y ≈ 8.46 log(x) + 6.62
Pour le montage de y = AeBx, prendre le logarithme des deux côtés donne log y = log Un + Bx. Tellement en forme (log y) contre x.
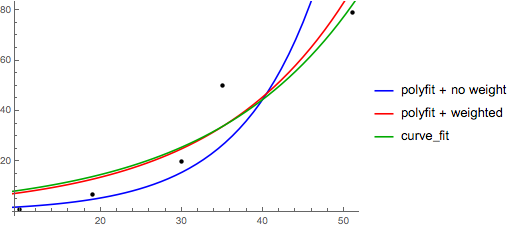
Notez que le montage (log y) que si elle est linéaire mettra l'accent sur les petites valeurs de y, provoquant une grande déviation pour les grandes y . C'est parce que polyfit (régression linéaire) fonctionne en minimisant les ∑j' (ΔY)2 = ∑j' (Yje - Ŷj')2. Lorsque Yj' = log yj', les résidus ΔYj' = Δ(log yj') ≈ Δyj' / |yj'|. Donc, même si polyfit fait une très mauvaise décision pour le grand y, "diviser par|y|" facteur de compensation pour elle, ce qui provoque polyfit favorise les petites valeurs.
Cela pourrait être atténué en donnant à chaque entrée un" poids " proportionnel à y . polyfit prend en charge les moindres carrés pondérés via l'argument de mot clé w.
>>> x = numpy.array([10, 19, 30, 35, 51])
>>> y = numpy.array([1, 7, 20, 50, 79])
>>> numpy.polyfit(x, numpy.log(y), 1)
array([ 0.10502711, -0.40116352])
# y ≈ exp(-0.401) * exp(0.105 * x) = 0.670 * exp(0.105 * x)
# (^ biased towards small values)
>>> numpy.polyfit(x, numpy.log(y), 1, w=numpy.sqrt(y))
array([ 0.06009446, 1.41648096])
# y ≈ exp(1.42) * exp(0.0601 * x) = 4.12 * exp(0.0601 * x)
# (^ not so biased)
Notez que Excel, LibreOffice et la plupart des scientifiques les calculatrices utilisent généralement la formule non pondérée (biaisée) pour les lignes de régression / tendance exponentielles. si vous voulez que vos résultats soient compatibles avec ces plateformes, n'incluez pas les pondérations même si elles donnent de meilleurs résultats.
Maintenant, si vous pouvez utiliser scipy, vous pouvez utiliser scipy.optimize.curve_fit pour s'adapter à n'importe quel modèle sans transformations.
Pour y = Un + B log x, le résultat est le même que la transformation méthode:
>>> x = numpy.array([1, 7, 20, 50, 79])
>>> y = numpy.array([10, 19, 30, 35, 51])
>>> scipy.optimize.curve_fit(lambda t,a,b: a+b*numpy.log(t), x, y)
(array([ 6.61867467, 8.46295606]),
array([[ 28.15948002, -7.89609542],
[ -7.89609542, 2.9857172 ]]))
# y ≈ 6.62 + 8.46 log(x)
Pour y = AeBx, cependant, nous pouvons obtenir un meilleur ajustement, car il calcule Δ(log y) directement. Mais nous devons fournir une supposition initialize afin que curve_fit puisse atteindre le minimum local souhaité.
>>> x = numpy.array([10, 19, 30, 35, 51])
>>> y = numpy.array([1, 7, 20, 50, 79])
>>> scipy.optimize.curve_fit(lambda t,a,b: a*numpy.exp(b*t), x, y)
(array([ 5.60728326e-21, 9.99993501e-01]),
array([[ 4.14809412e-27, -1.45078961e-08],
[ -1.45078961e-08, 5.07411462e+10]]))
# oops, definitely wrong.
>>> scipy.optimize.curve_fit(lambda t,a,b: a*numpy.exp(b*t), x, y, p0=(4, 0.1))
(array([ 4.88003249, 0.05531256]),
array([[ 1.01261314e+01, -4.31940132e-02],
[ -4.31940132e-02, 1.91188656e-04]]))
# y ≈ 4.88 exp(0.0553 x). much better.
Vous pouvez également adapter un ensemble de données à la fonction que vous aimez utiliser curve_fit à partir de scipy.optimize. Par exemple, si vous voulez adapter une fonction exponentielle (à partir de la documentation ):
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
def func(x, a, b, c):
return a * np.exp(-b * x) + c
x = np.linspace(0,4,50)
y = func(x, 2.5, 1.3, 0.5)
yn = y + 0.2*np.random.normal(size=len(x))
popt, pcov = curve_fit(func, x, yn)
, puis si vous voulez tracer, vous pouvez faire:
plt.figure()
plt.plot(x, yn, 'ko', label="Original Noised Data")
plt.plot(x, func(x, *popt), 'r-', label="Fitted Curve")
plt.legend()
plt.show()
(Remarque: la * en face de popt lorsque vous tracez permettra d'élargir les conditions dans le a, b, et c que func attendait.)
J'avais des problèmes avec cela, alors laissez - moi être très explicite pour que noobs comme moi puisse comprendre.
Disons que nous avons un fichier de données ou quelque chose comme ça
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
import numpy as np
import sympy as sym
"""
Generate some data, let's imagine that you already have this.
"""
x = np.linspace(0, 3, 50)
y = np.exp(x)
"""
Plot your data
"""
plt.plot(x, y, 'ro',label="Original Data")
"""
brutal force to avoid errors
"""
x = np.array(x, dtype=float) #transform your data in a numpy array of floats
y = np.array(y, dtype=float) #so the curve_fit can work
"""
create a function to fit with your data. a, b, c and d are the coefficients
that curve_fit will calculate for you.
In this part you need to guess and/or use mathematical knowledge to find
a function that resembles your data
"""
def func(x, a, b, c, d):
return a*x**3 + b*x**2 +c*x + d
"""
make the curve_fit
"""
popt, pcov = curve_fit(func, x, y)
"""
The result is:
popt[0] = a , popt[1] = b, popt[2] = c and popt[3] = d of the function,
so f(x) = popt[0]*x**3 + popt[1]*x**2 + popt[2]*x + popt[3].
"""
print "a = %s , b = %s, c = %s, d = %s" % (popt[0], popt[1], popt[2], popt[3])
"""
Use sympy to generate the latex sintax of the function
"""
xs = sym.Symbol('\lambda')
tex = sym.latex(func(xs,*popt)).replace('$', '')
plt.title(r'$f(\lambda)= %s$' %(tex),fontsize=16)
"""
Print the coefficients and plot the funcion.
"""
plt.plot(x, func(x, *popt), label="Fitted Curve") #same as line above \/
#plt.plot(x, popt[0]*x**3 + popt[1]*x**2 + popt[2]*x + popt[3], label="Fitted Curve")
plt.legend(loc='upper left')
plt.show()
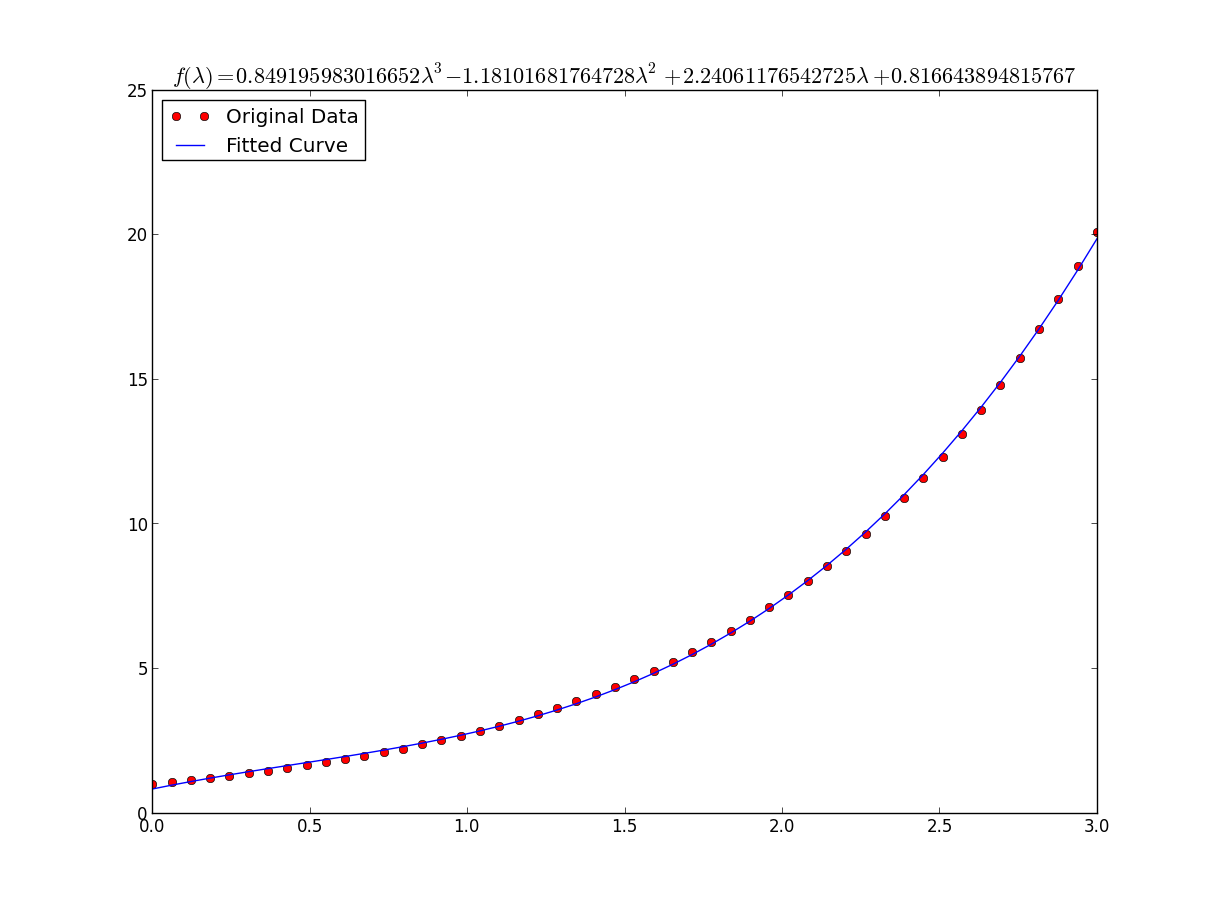
Le résultat est: a = 0,849195983017, b = -1.18101681765, c = 2,24061176543, d = 0,816643894816
Eh Bien, je suppose que vous pouvez toujours utiliser:
np.log --> natural log
np.log10 --> base 10
np.log2 --> base 2
Modifier légèrement la réponse de IanVS :
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
def func(x, a, b, c):
#return a * np.exp(-b * x) + c
return a * np.log(b * x) + c
x = np.linspace(1,5,50) # changed boundary conditions to avoid division by 0
y = func(x, 2.5, 1.3, 0.5)
yn = y + 0.2*np.random.normal(size=len(x))
popt, pcov = curve_fit(func, x, yn)
plt.figure()
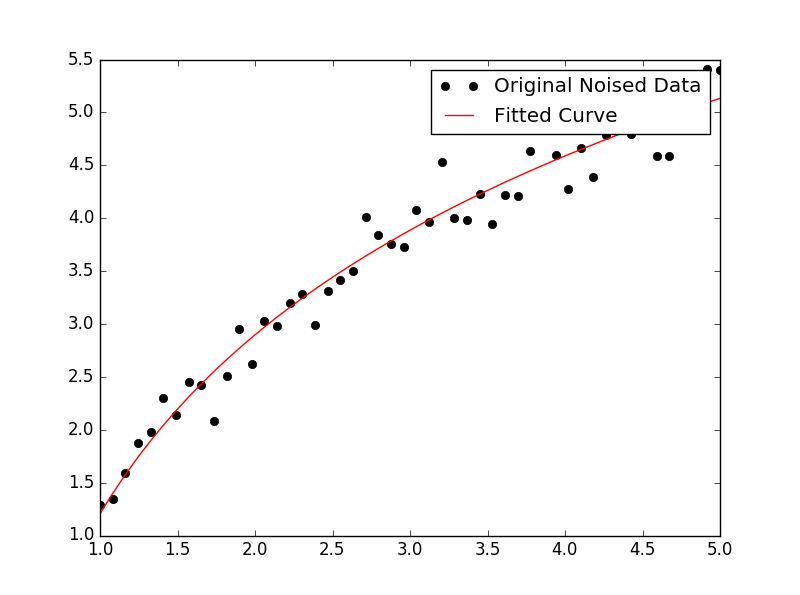
plt.plot(x, yn, 'ko', label="Original Noised Data")
plt.plot(x, func(x, *popt), 'r-', label="Fitted Curve")
plt.legend()
plt.show()
Il en résulte le graphique suivant: