Comment diviser le polygone irrégulier en zones égales sur Google map V2
je suis en train de développer une application pour échantillonner Glebe dans un but agricole. En ce qu'un utilisateur peut sélectionner un a Glebe en tapant sur la carte qui créera un polygone en fonction du nombre de robinets. Je suis capable de créer ce polygone et d'obtenir la zone du polygone. Mais maintenant je dois le diviser en zones égales.
par exemple, si la surface du polygone est de 50 m ^ 2, alors il sera divisé en 50 zones de 1 m^2. La même fonctionnalité a été faite dans Agric Precision App. Trouver l'image ci-dessous. Je dois diviser le polygone de la même façon que l'image ci-dessous et montrer les points à l'intérieur.
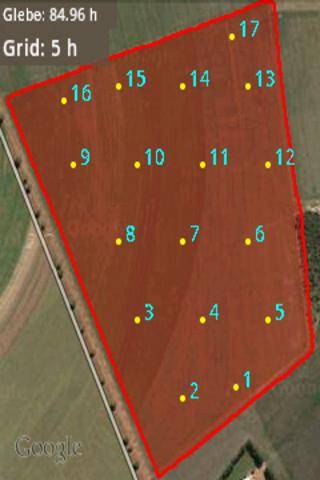
Pour obtenir de la Région, je suis à l'aide de Google Map Utilty Lib il a une algue aussi pour le Clustering de grille. Je veux même comme l'image ci-dessus. Dans l'image ci-dessus, ils ont divisé la superficie par 5 Hectares. Étant donné que toute la superficie est de 85 Hectares, le total des points doit donc être indiqué sera de 17. Qu'est ce que la Façon dont il fonctionne.
donc mon la question est:
comment trouver ces points selon la zone du polygone sur la carte pour que je puisse les dessiner sur la carte?
2 réponses
aucune contrainte n'a été donnée sur la forme des glèbes, donc voici une solution qui remplira l'énoncé du problème en construisant une décomposition en forme d'étoile. Il suppose que le polygone est convexe:
sélectionnez arbitrairement un vertex principal.
trianguler le polygone en joignant le sommet principal à chaque bord à tour de rôle, donnant des triangles de zones
A1,A2,A3...Commencer un voyage autour du polygone, à partir du sommet principal. Si le premier triangle est plus grand que la zone désirée (
A1 > A), trouver le point le long du bord tel qu'il subdivisera le triangle en un sous-triangle de la zone désirée. Continuer le voyage à partir d'ici avec le sous-triangle restant (ayant la zoneA1-A). Sinon, soustrayez la zone du premier triangle de la zone désirée et continuez le voyage (AA-A1).
C'est très similaire au fractionnement d'un séquence de N intervalles sur la ligne réelle dans K intervalles de longueur égale.
a mon avis, une décomposition en étoile ne vous conviendra pas.
si votre polygone est convexe, une solution peut être obtenue en résolvant le sous-problème suivant: "Etant donné un polygone convexe de la zone A, trouvez la ligne horizontale qui le divise en deux parties des zones respectives B et a-B."
cela se fait facilement en balayant les sommets de haut en bas avec un mouvement horizontal et en calculant la surface couverte (cela forme une décomposition du polygone en trapézoïdes). À un certain point, vous dépasserez la zone B. par interpolation linéaire entre les les vertex actuels et précédents, vous déterminerez l'ordonnée exacte de l'horizontale.
vous utiliserez la solution du sous-problème comme suit:
1) calculer la racine carrée entière, Let N, du nombre de tuiles désirées, let M.
2) Couper le polygone N fois, chaque fois obtenir la surface de n tuiles. Il y aura un reste de tuiles M-N^2.
3) trancher chaque tranche à l'aide de verticales pour singuler les tuiles finales.
les carreaux aura une forme beaucoup plus acceptable (rectangles quand ils ne rencontrent aucun bord).