Comment afficher un graphique 3D d'un tableau 3D isosurface dans matplotlib mplot3D ou similaire?
j'ai une matrice tridimensionnelle. J'aimerais afficher (en matplotlib) un joli tracé 3D d'une isosurface de ce tableau (ou plus strictement, afficher une isosurface du champ scalaire 3D défini par interpolation entre les points échantillons).
la partie mplot3d de matplotlib fournit un support de graphique 3D agréable, mais (pour autant que je puisse voir) son API n'a rien qui va simplement prendre un tableau 3D de valeurs scalaires et afficher une isosurface. Cependant, il prend en charge l'affichage d'un collection de polygones, donc probablement je pourrais mettre en œuvre l'algorithme des cubes de marche pour générer de tels polygones.
il semble tout à fait probable qu'un scipy-friendly cubes de marche a déjà été mis en œuvre quelque part et que je ne l'ai pas trouvé, ou que je manque une certaine façon facile de le faire. Alternativement, je serais heureux de n'importe quels pointeurs vers d'autres outils pour visualiser les données 3D array facilement utilisables du monde Python/num PY/scipy.
3 réponses
juste pour développer mon commentaire ci-dessus, le tracé 3D de matplotlib n'est pas vraiment destiné à quelque chose d'aussi complexe que les isosurfaces. Il est destiné à produire de belles publications vectorielles de qualité pour des tracés 3D vraiment simples. Il ne peut pas gérer les polygones 3D complexes, donc même s'il est implémenté des cubes marchant vous - même pour créer l'isosurface, il ne le rendrait pas correctement.
Toutefois, ce que vous pouvez faire est d'utiliser mayavi (Mlab API c'est un peu plus pratique que d'utiliser directement mayavi), qui utilise VTK traiter et visualiser des données multidimensionnelles.
comme exemple rapide (modifié à partir d'un des exemples de la galerie mayavi):
import numpy as np
from enthought.mayavi import mlab
x, y, z = np.ogrid[-10:10:20j, -10:10:20j, -10:10:20j]
s = np.sin(x*y*z)/(x*y*z)
src = mlab.pipeline.scalar_field(s)
mlab.pipeline.iso_surface(src, contours=[s.min()+0.1*s.ptp(), ], opacity=0.3)
mlab.pipeline.iso_surface(src, contours=[s.max()-0.1*s.ptp(), ],)
mlab.show()

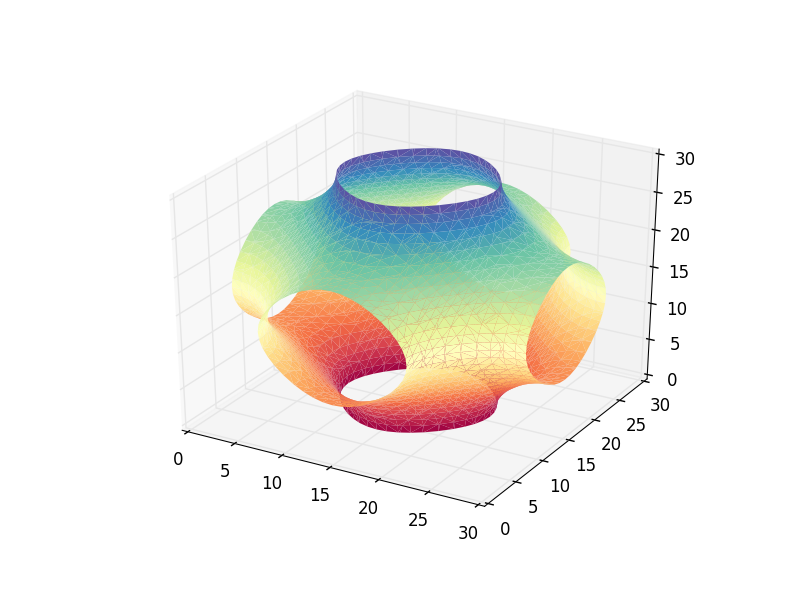
en complément de la réponse de @DanHickstein, vous pouvez aussi utiliser trisurf pour visualiser les polygones obtenus dans la phase des cubes de marche.
import numpy as np
from numpy import sin, cos, pi
from skimage import measure
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def fun(x, y, z):
return cos(x) + cos(y) + cos(z)
x, y, z = pi*np.mgrid[-1:1:31j, -1:1:31j, -1:1:31j]
vol = fun(x, y, z)
verts, faces = measure.marching_cubes(vol, 0, spacing=(0.1, 0.1, 0.1))
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_trisurf(verts[:, 0], verts[:,1], faces, verts[:, 2],
cmap='Spectral', lw=1)
plt.show()
Mise À Jour: 11 Mai 2018
comme mentionné par @DrBwts, marching_cubes retourne maintenant 4 valeurs. Le code suivant fonctionne.
import numpy as np
from numpy import sin, cos, pi
from skimage import measure
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def fun(x, y, z):
return cos(x) + cos(y) + cos(z)
x, y, z = pi*np.mgrid[-1:1:31j, -1:1:31j, -1:1:31j]
vol = fun(x, y, z)
verts, faces, _, _ = measure.marching_cubes(vol, 0, spacing=(0.1, 0.1, 0.1))
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_trisurf(verts[:, 0], verts[:,1], faces, verts[:, 2],
cmap='Spectral', lw=1)
plt.show()
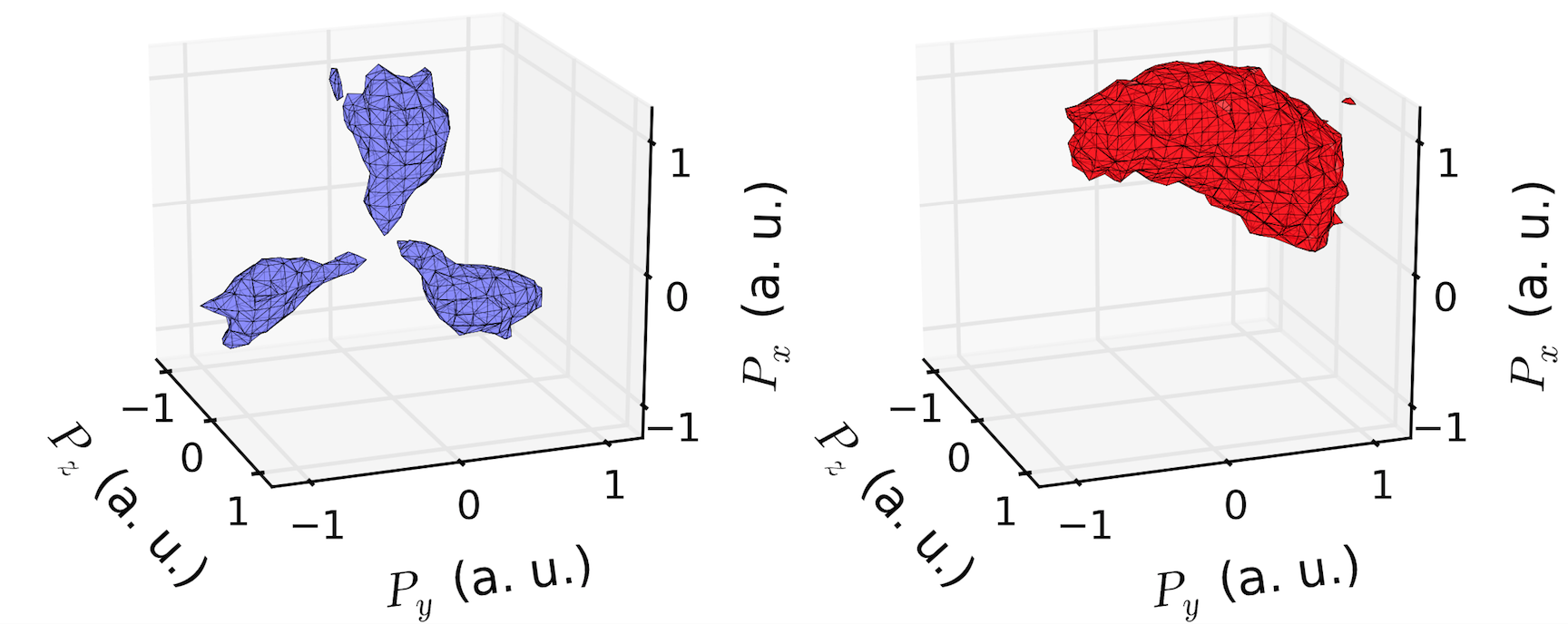
si vous voulez garder vos parcelles dans matplotlib( beaucoup plus facile de produire des images de qualité de publication que mayavi à mon avis), alors vous pouvez utiliser le fonction marching_cubes implémentée dans skimage et ensuite tracer les résultats dans matplotlib en utilisant
mpl_toolkits.mplot3d.art3d.Poly3DCollection
comme indiqué dans le lien ci-dessus. Matplotlib fait un très bon travail de rendu de l'isosurface. Voici un exemple que j'ai fait d'une véritable tomographie données: