Comment déterminer quelle est la fonction de distribution de probabilité d'un tableau de numpy?
j'ai cherché autour et à ma surprise il semble que cette question n'a pas été répondue.
j'ai un tableau Numpy contenant 10000 valeurs de mesures. J'ai tracé un histogramme avec Matplotlib, et par inspection visuelle, les valeurs semblent être distribuées normalement:
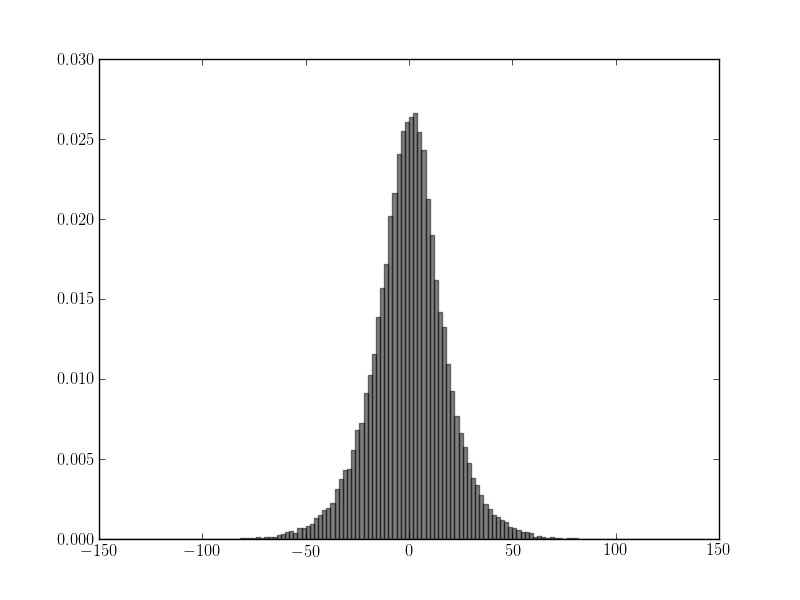
cependant, je voudrais valider ceci. J'ai trouvé un test de normalité implémenté sous scipy.statistique.mstats.normaltest, mais le résultat dit le contraire. J'obtiens ce résultat:
(masked_array(data = [1472.8855375088663],
mask = [False],
fill_value = 1e+20)
, masked_array(data = [ 0.],
mask = False,
fill_value = 1e+20)
)
ce qui signifie que les chances que l'ensemble de données soit normalement distribué sont 0. J'ai repris les expériences et je les ai testées de nouveau pour obtenir le même résultat, et dans le "meilleur" cas, la valeur p était de 3,0 e-290.
j'ai testé la fonction avec le code suivant et il semble faire ce que je veux:
import numpy
import scipy.stats as stats
mu, sigma = 0, 0.1
s = numpy.random.normal(mu, sigma, 10000)
print stats.normaltest(s)
(1.0491016699730547, 0.59182113002186942)
Si j'ai bien compris et utilisé la fonction correctement, cela signifie que les valeurs ne sont normalement pas distribués. (Et honnêtement je n'ai aucune idée pourquoi il y a une différence dans la sortie, c.-à-d. moins de détails.)
j'étais assez sûr qu'il s'agissait d'une distribution normale (bien que ma connaissance des statistiques soit élémentaire), et je ne sais pas quelle pourrait être l'alternative. Comment puis-je vérifier quelle est la fonction de distribution de probabilité en question?
EDIT:
mon tableau de Numpy contenant 10000 valeurs est généré comme ceci (je sais que ce n'est pas la meilleure façon de remplir un tableau Numpy), et ensuite de la normaltest est de lancer:
values = numpy.empty(shape=10000, 1))
for i in range(0, 10000):
values[i] = measurement(...) # The function returns a float
print normaltest(values)
EDIT 2:
je viens de réaliser que l'écart entre les sorties est parce que j'ai utilisés par inadvertance deux fonctions différentes (scipy.statistique.normaltest () et scipy.statistique.mstats.normaltest ()), mais cela ne fait pas de différence puisque la partie pertinente de la sortie est la même quelle que soit la fonction utilisée.
modifier 3:
ajustement de l'histogramme avec la suggestion d'askewchan:
plt.plot(bin_edges, scipy.stats.norm.pdf(bin_edges, loc=values.mean(), scale=values.std()))
résultats:
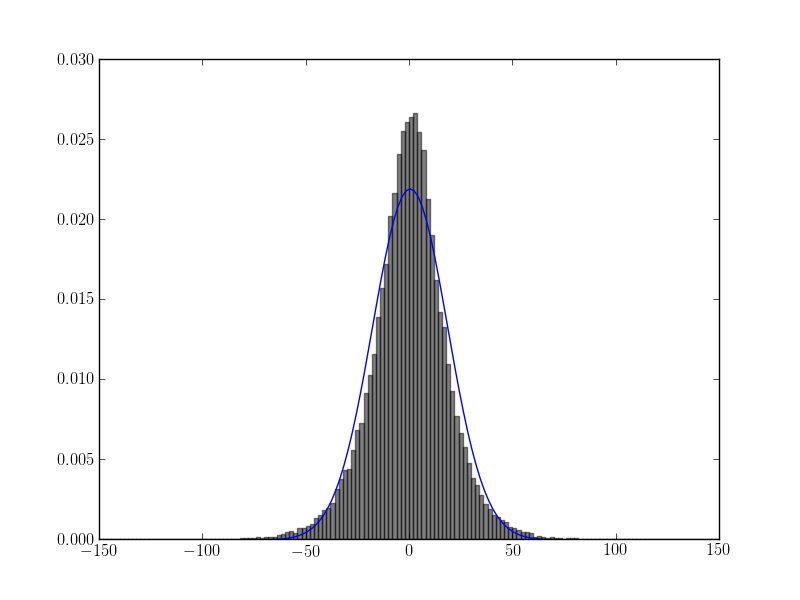
EDIT 4:
ajuster l'histogramme avec la suggestion de l'utilisateur user333700:
scipy.stats.t.fit(data)
résultats:
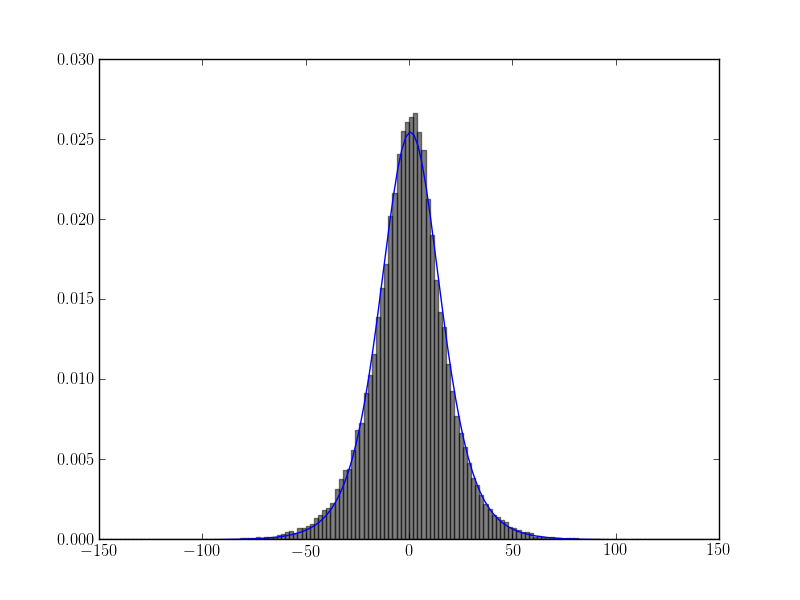
1 réponses
en Supposant que vous avez utilisé le test correctement, je suppose que vous avez un petits déviation par rapport à une distribution normale et parce que la taille de votre échantillon est si grande, même de petites déviations conduiront à un rejet de l'hypothèse nulle d'une distribution normale.
une possibilité est d'inspecter visuellement vos données en traçant un normed histogramme avec un grand nombre de bacs et le pdf loc=data.mean() et scale=data.std().
il existe un autre test pour testing normality, stats models a des tests Anderson-Darling et Lillifors (Kolmogorov-Smirnov) lorsque les paramètres de distribution sont estimés.
cependant, je m'attends à ce que les résultats ne diffèrent pas beaucoup étant donné la Grande Taille de l'échantillon.
La question principale est de savoir si vous voulez savoir si votre échantillon est "exactement" à partir d'une distribution normale, ou si vous êtes simplement intéressé à savoir si votre échantillon provient d'une distribution qui est très proche de la normale distribution,fermer en termes d'usage pratique.
pour développer sur le dernier point:
http://jpktd.blogspot.ca/2012/10/tost-statistically-significant.html http://www.graphpad.com/guides/prism/6/statistics/index.htm?testing_for_equivalence2.htm
comme la taille de l'échantillon augmente un test d'hypothèse gagne plus de puissance, cela signifie que le test sera en mesure de rejeter l'hypothèse nulle de l'égalité même pour de plus en plus petites différences. Si nous maintenons notre niveau de signification fixe, Nous finirons par rejeter les petites différences dont nous ne nous soucions pas vraiment.
un autre type de test d'hypothèse est celui où nous voulons montrer que notre échantillon est proche de l'hypothèse ponctuelle donnée, par exemple deux échantillons ont presque la même moyenne. Le problème est que nous devons définir ce qu'est notre région d'équivalence.
dans le cas de tests de la qualité de l'ajustement, nous devons choisir une distance mesurer et définir un seuil pour la mesure de la distance entre l'échantillon et la distribution hypothétique. Je n'ai trouvé aucune explication où l'intuition pourrait aider à choisir ce seuil de distance.
statistiques.normaltest est basé sur les déviations de la asymétrie et kurtosis de ceux de la distribution normale.
Anderson-Darling est basé sur une intégrale des différences quadratiques pondérées entre les cdf.
Kolmogorov-Smirnov est basé sur le maximum différence absolue entre les cdf.
chisquare pour la mise à la poubelle de données serait basé sur la somme pondérée des carrés des bin probabilités.
et ainsi de suite.
j'ai seulement essayé les tests d'équivalence avec des données en série ou discrétisées, où j'ai utilisé un seuil de quelques cas de référence qui était encore assez arbitraire.
dans les tests d'équivalence médicale, il existe des normes prédéfinies pour préciser quand deux traitements peuvent être considérés comme équivalents, ou de la même façon, comme inférieur ou supérieur dans la version unilatérale.