Comment déterminer si une liste de points polygones est dans le sens des aiguilles d'une montre?

commence par un des sommets, et calcule l'angle sous-tendu de chaque côté.

le premier et Le dernier sera égal à zéro (donc ignorer ces); pour le reste, le sinus de l'angle sera donné par le produit vectoriel des normalisations pour unité de longueur (point[n]-[0]) et ([n-1]-[0]).

si la somme des valeurs est positive, alors votre polygone est dessiné dans le sens anti-horaire.

pour ce que ça vaut, j'ai utilisé ce mixin pour calculer l'ordre d'enroulement des applications V3 de L'API GoogleMaps.

le code tire parti de l'effet secondaire des surfaces polygonales: un ordre d'enroulement des vertex dans le sens des aiguilles d'une montre produit une surface positive, tandis qu'un ordre d'enroulement des mêmes vertex dans le sens contraire des aiguilles d'une montre produit la même surface qu'une valeur négative. Le code utilise également une sorte d'API privée dans la bibliothèque de géométrie de Google Maps. Je me suis sentie à l'aise de l'utiliser à vos risques et périls.

exemple d'utilisation:

var myPolygon = new google.maps.Polygon({/*options*/});
var isCW = myPolygon.isPathClockwise();

exemple Complet avec les tests unitaires @ http://jsfiddle.net/stevejansen/bq2ec/

/** Mixin to extend the behavior of the Google Maps JS API Polygon type
 *  to determine if a polygon path has clockwise of counter-clockwise winding order.
 *  
 *  Tested against v3.14 of the GMaps API.
 *
 *  @author  stevejansen_github@icloud.com
 *
 *  @license http://opensource.org/licenses/MIT
 *
 *  @version 1.0
 *
 *  @mixin
 *  
 *  @param {(number|Array|google.maps.MVCArray)} [path] - an optional polygon path; defaults to the first path of the polygon
 *  @returns {boolean} true if the path is clockwise; false if the path is counter-clockwise
 */
(function() {
  var category = 'google.maps.Polygon.isPathClockwise';
     // check that the GMaps API was already loaded
  if (null == google || null == google.maps || null == google.maps.Polygon) {
    console.error(category, 'Google Maps API not found');
    return;
  }
  if (typeof(google.maps.geometry.spherical.computeArea) !== 'function') {
    console.error(category, 'Google Maps geometry library not found');
    return;
  }

  if (typeof(google.maps.geometry.spherical.computeSignedArea) !== 'function') {
    console.error(category, 'Google Maps geometry library private function computeSignedArea() is missing; this may break this mixin');
  }

  function isPathClockwise(path) {
    var self = this,
        isCounterClockwise;

    if (null === path)
      throw new Error('Path is optional, but cannot be null');

    // default to the first path
    if (arguments.length === 0)
        path = self.getPath();

    // support for passing an index number to a path
    if (typeof(path) === 'number')
        path = self.getPaths().getAt(path);

    if (!path instanceof Array && !path instanceof google.maps.MVCArray)
      throw new Error('Path must be an Array or MVCArray');

    // negative polygon areas have counter-clockwise paths
    isCounterClockwise = (google.maps.geometry.spherical.computeSignedArea(path) < 0);

    return (!isCounterClockwise);
  }

  if (typeof(google.maps.Polygon.prototype.isPathClockwise) !== 'function') {
    google.maps.Polygon.prototype.isPathClockwise = isPathClockwise;
  }
})();

Une mise en œuvre de de Sean réponse JavaScript:

function calcArea(poly) {
    if(!poly || poly.length < 3) return null;
    let end = poly.length - 1;
    let sum = poly[end][0]*poly[0][1] - poly[0][0]*poly[end][1];
    for(let i=0; i<end; ++i) {
        const n=i+1;
        sum += poly[i][0]*poly[n][1] - poly[n][0]*poly[i][1];
    }
    return sum;
}

function isClockwise(poly) {
    return calcArea(poly) > 0;
}

let poly = [[352,168],[305,208],[312,256],[366,287],[434,248],[416,186]];

console.log(isClockwise(poly));

let poly2 = [[618,186],[650,170],[701,179],[716,207],[708,247],[666,259],[637,246],[615,219]];

console.log(isClockwise(poly2));

Je suis sûr que c'est juste. Il semble être au travail :-)

ces polygones ressemblent à ceci, si vous vous demandez:

si vous utilisez Matlab, la fonction ispolycw retourne true si les sommets des polygones sont dans le sens des aiguilles d'une montre.

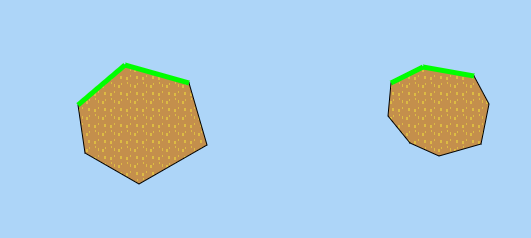
comme aussi expliqué dans cet article de Wikipedia orientation de la courbe , donné 3 points p , q et r sur le plan (i.e. avec des coordonnées x et y), Vous pouvez calculer le signe du déterminant suivant

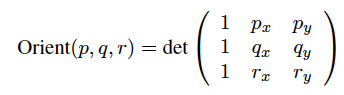
si le déterminant est négatif (c.-à-d. Orient(p, q, r) < 0 ), alors le polygone est orienté dans le sens des aiguilles d'une montre (CW). Si le déterminant est positif (c'est à dire Orient(p, q, r) > 0 ), le polygone est orienté dans le sens inverse des aiguilles d'une montre (CCW). Le déterminant est zéro (c'est-à-dire Orient(p, q, r) == 0 ) si les points p , q et r sont collinéaire .

dans la formule ci-dessus, nous préparons ceux en face des coordonnées de p , q et r parce que nous utilisons des coordonnées homogènes .

c'est la fonction implémentée pour OpenLayers 2 . La condition pour avoir un polygone dans le sens des aiguilles d'une montre est area < 0 , il a confirmé par cette référence .

function IsClockwise(feature)
{
    if(feature.geometry == null)
        return -1;

    var vertices = feature.geometry.getVertices();
    var area = 0;

    for (var i = 0; i < (vertices.length); i++) {
        j = (i + 1) % vertices.length;

        area += vertices[i].x * vertices[j].y;
        area -= vertices[j].x * vertices[i].y;
        // console.log(area);
    }

    return (area < 0);
}

je pense que pour certains points dans le sens des aiguilles toutes les arêtes doivent être positifs, non seulement la somme des bords. Si un bord est négatif, au moins 3 points sont donnés dans le sens contraire des aiguilles d'une montre.

ma solution c# / LINQ est basée sur le Conseil produit croisé de @charlesbretana ci-dessous. Vous pouvez spécifier une référence normale pour le remontage. Il devrait fonctionner aussi longtemps que la courbe est la plupart du temps dans le plan défini par le vecteur.

using System.Collections.Generic;
using System.Linq;
using System.Numerics;

namespace SolidworksAddinFramework.Geometry
{
    public static class PlanePolygon
    {
        /// <summary>
        /// Assumes that polygon is closed, ie first and last points are the same
        /// </summary>
       public static bool Orientation
           (this IEnumerable<Vector3> polygon, Vector3 up)
        {
            var sum = polygon
                .Buffer(2, 1) // from Interactive Extensions Nuget Pkg
                .Where(b => b.Count == 2)
                .Aggregate
                  ( Vector3.Zero
                  , (p, b) => p + Vector3.Cross(b[0], b[1])
                                  /b[0].Length()/b[1].Length());

            return Vector3.Dot(up, sum) > 0;

        } 

    }
}

avec un essai unitaire

namespace SolidworksAddinFramework.Spec.Geometry
{
    public class PlanePolygonSpec
    {
        [Fact]
        public void OrientationShouldWork()
        {

            var points = Sequences.LinSpace(0, Math.PI*2, 100)
                .Select(t => new Vector3((float) Math.Cos(t), (float) Math.Sin(t), 0))
                .ToList();

            points.Orientation(Vector3.UnitZ).Should().BeTrue();
            points.Reverse();
            points.Orientation(Vector3.UnitZ).Should().BeFalse();



        } 
    }
}

C'est ma solution en utilisant les explications dans les autres réponses:

def segments(poly):
    """A sequence of (x,y) numeric coordinates pairs """
    return zip(poly, poly[1:] + [poly[0]])

def check_clockwise(poly):
    clockwise = False
    if (sum(x0*y1 - x1*y0 for ((x0, y0), (x1, y1)) in segments(poly))) < 0:
        clockwise = not clockwise
    return clockwise

poly = [(2,2),(6,2),(6,6),(2,6)]
check_clockwise(poly)
False

poly = [(2, 6), (6, 6), (6, 2), (2, 2)]
check_clockwise(poly)
True

une méthode beaucoup plus simple de calcul, si vous connaissez déjà un point à l'intérieur du polygone :

1. choisissez un segment de ligne du polygone original, les points et leurs coordonnées dans cet ordre.

2. Ajouter un point" intérieur " et former un triangle.

3. calculer CW ou CCW comme suggéré ici avec ces trois points.

après avoir testé plusieurs implémentations non fiables, l'algorithme qui a fourni des résultats satisfaisants concernant l'orientation de la CW/CCW était celui, posté par OP dans ce" thread 151930920 "( shoelace_formula_3 ).

voici la solution swift 3.0 basée sur les réponses ci-dessus:

    for (i, point) in allPoints.enumerated() {
        let nextPoint = i == allPoints.count - 1 ? allPoints[0] : allPoints[i+1]
        signedArea += (point.x * nextPoint.y - nextPoint.x * point.y)
    }

    let clockwise  = signedArea < 0

une autre solution pour cela;

const isClockwise = (vertices=[]) => {
    const len = vertices.length;
    const sum = vertices.map(({x, y}, index) => {
        let nextIndex = index + 1;
        if (nextIndex === len) nextIndex = 0;

        return {
            x1: x,
            x2: vertices[nextIndex].x,
            y1: x,
            y2: vertices[nextIndex].x
        }
    }).map(({ x1, x2, y1, y2}) => ((x2 - x1) * (y1 + y2))).reduce((a, b) => a + b);

    if (sum > -1) return true;
    if (sum < 0) return false;
}

prenez tous les sommets comme un tableau comme celui-ci;

const vertices = [{x: 5, y: 0}, {x: 6, y: 4}, {x: 4, y: 5}, {x: 1, y: 5}, {x: 1, y: 0}];
isClockwise(vertices);

Solution pour R pour déterminer la direction et l'inverse si des aiguilles d'une montre (jugé nécessaire pour owin objets):

coords <- cbind(x = c(5,6,4,1,1),y = c(0,4,5,5,0))
a <- numeric()
for (i in 1:dim(coords)[1]){
  #print(i)
  q <- i + 1
  if (i == (dim(coords)[1])) q <- 1
  out <- ((coords[q,1]) - (coords[i,1])) * ((coords[q,2]) + (coords[i,2]))
  a[q] <- out
  rm(q,out)
} #end i loop

rm(i)

a <- sum(a) #-ve is anti-clockwise

b <- cbind(x = rev(coords[,1]), y = rev(coords[,2]))

if (a>0) coords <- b #reverses coords if polygon not traced in anti-clockwise direction

trouver le centre de masse de ces points.

supposez qu'il y ait des lignes de ce point à vos points.

trouver l'angle entre deux lignes pour la ligne0 ligne 1

que pour la ligne 1 et la ligne 2

...

...

si cet angle augmente de façon monotone qu'il est dans le sens contraire des aiguilles d'une montre,

autrement si monotone le décroissant est dans le sens des aiguilles d'une montre

d'autre (il n'est pas monotonical)

vous ne pouvez pas décider, donc il n'est pas sage