Comment détecter si une ellipse se croise (entre en collision avec) un cercle

une ellipse est définie par l'ensemble des points dont la somme de la distance au point A et de la distance au point B est constante E. (A et B sont appelés les foyers de l'ellipse).

tous les points P, dont la somme AP + BP est inférieure à e, se situent à l'intérieur de l'ellipse.

Un cercle est défini comme l'ensemble des points dont l' distance jusqu'au point c est R.

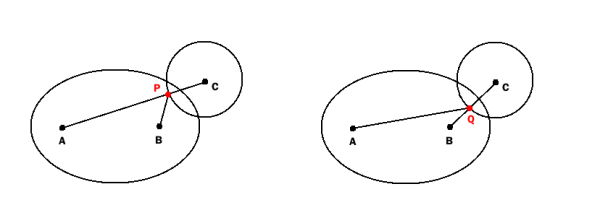
Un test simple pour l'intersection du cercle et de l'ellipse est la suivante:

Trouver

P comme l' intersection du cercle et de la ligne AC et

Q à l'intersection du cercle et de la ligne BC.

Cercle et de l'ellipse se croisent (ou le cercle se trouve complètement à l'intérieur de l'ellipse) si

AP + BP < = e ou AQ + BQ < = e

EDIT:

après le commentaire de Martin DeMello et l'adaptation de ma réponse en conséquence, j'ai réfléchi davantage sur le problème et a constaté que la réponse (avec le 2e contrôle) ne détecte toujours pas intersections:

si le cercle et l'ellipse ne se croisent que très peu (juste un peu plus que tangente) P et Q Ne se trouveront pas à l'intérieur de l'ellipse:

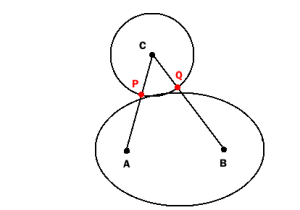
Donc, le test décrit ci-dessus détecte la collision seulement si le chevauchement est "assez grand". Peut-être est-il assez bon pour vos fins pratiques, bien que mathématiquement, il n'est pas parfait.

agrandir les rayons majeurs et mineurs de l'ellipse par le rayon du cercle. Testez ensuite si le centre du cercle donné est à l'intérieur de cette nouvelle ellipse plus grande en additionnant les distances aux foyers de l'ellipse agrandie.

Cet algorithme est très efficace. Vous pouvez commencer si le cercle donné ne coupe pas un cercle qui circonscrit l'ellipse. C'est plus lent qu'un test de boxe, mais trouver la boxe d'une ellipse non alignée sur l'axe est délicat.

trouver le point sur l'ellipse le plus proche du centre du cercle

et puis vérifiez si la distance de ce point est plus petite que le rayon du cercle

si vous avez besoin d'aide juste un commentaire, mais c'est tout simplement le calcul

edit: voici un moyen de trouver la solution, puisqu'il y a quelque chose qui ne va pas avec les caillés

donnée au centre α β sur l'ellipse

et (faute de se souvenir du terme) rayon X a, y rayon B la paramétrisation est

r (Θ) = (ab)/ ((BcosΘ)^2 + (asinΘ)^2)^.5)

x (Θ) = α + sin (Θ)r (Θ)

y (Θ) = β + cos (Θ)r (Θ)

et puis il suffit de prendre le cercle avec le centre à (φ, ψ) et le rayon r puis la distance d (Θ) = ((φ - x(Θ))^2 + (ψ - y(Θ)) ^2)^.5

le minimum de cette distance est lorsque d'(Θ) = 0 (' pour la dérivée)

d'(Θ) = 1 / d (Θ) * (- φx'(Θ) + x (Θ)x '(Θ) - ψy'(Θ) + y (Θ)y'(Θ)) )

= = >

x'(Θ) * (- φ + x (Θ)) = y'(Θ) * (ψ-y (Θ))

et continuer à aller et aller et j'espère que vous pourrez résoudre pour Θ

Le cadre dans lequel vous travaillez peut avoir des choses pour vous aider à résoudre ce problème, et vous pouvez toujours prendre la solution facile et approximatif roots via méthode de Newton

si un cercle et une ellipse entrent en collision, alors soit leurs limites se croisent 1, 2, 3, ou 4 fois(ou à l'infini dans le cas d'une ellipse circulaire qui coïncide avec le cercle), ou le cercle est à l'intérieur de l'ellipse ou vice versa.

je suis en supposant que le cercle a une équation de (x - a)^2 + (y - b)^2 <= r^2 (1) et l'ellipse a une équation de [(x - c)^2]/[d^2] + [(y - e)^2]/[f^2] <= 1 (2)

Pour vérifier si l'un d'entre eux est à l'intérieur de l'autre, vous pouvez evaluer l'équation du cercle aux coordonnées du centre de l'ellipse(x=c, y=e), ou vice versa, et voir si l'inégalité tient.

pour vérifier les autres cas dans lesquels leurs limites se croisent, vous devez vérifier si le système d'équations décrit par (1) et (2) a des solutions.

vous pouvez le faire en ajoutant (1) et (2), vous donnant

(x - a)^2 + (y - b)^2 + [(x - c)^2]/[d^2] + [(y - e)^2]/[f^2] = r^2 + 1

ensuite, vous multipliez les termes, en donnant

x^2 - 2ax + a^2 + y^2 - 2by + b^2 + x^2/d^2 - 2cx/d^2 + c^2/d^2 + y^2/f^2 - 2ey/f^2 + e^2/f^2 = r^2 + 1

collectionner comme les termes, nous obtenons

(1 + 1/d^2)x^2 - (2a + 2c/d^2)x + (1 + 1/f^2)y^2 - (2b + 2e/f^2)y = 1 + r^2 - a^2 - b^2 - c^2/d^2 - e^2/f^2

maintenant, laissez -m = (1 + 1/d^2), n = -(2a + 2c/d^2), o = (1 + 1/f^2), and p = -(2b + 2e/f^2)

l'équation est maintenant mx^2 + nx + oy^2 + py = 1 + r^2 - a^2 - b^2 - c^2/d^2 - e^2/f^2

maintenant, nous avons besoin de compléter les cases sur le côté gauche

m[x^2 + (n/m)x] + o[y^2 + (p/o)y] = 1 + r^2 - a^2 - b^2 - c^2/d^2 - e^2/f^2

m[x^2 + (n/m)x + (n/2m)^2 - (n/2m)^2] + o[y^2 + (p/o)y + (p/2o)^2 - (p/2o)^2] = 1 + r^2 - a^2 - b^2 - c^2/d^2 - e^2/f^2

m[(x + n/2m)^2 - (n/2m)^2] + o[(y + p/2o)^2 - (p/2o)^2] = 1 + r^2 - a^2 - b^2 - c^2/d^2 - e^2/f^2

m(x + n/2m)^2 - m(n/2m)^2 + o(y + p/2o)^2 - o(p/2o)^2 = 1 + r^2 - a^2 - b^2 - c^2/d^2 - e^2/f^2

m(x + n/2m)^2 + o(y + p/2o)^2 = 1 + r^2 - a^2 - b^2 - c^2/d^2 - e^2/f^2 + m(n/2m)^2 + o(p/2o)^2

ce système a une solution iff 11 + r^2 - a^2 - b^2 - c^2/d^2 - e^2/f^2 + m(n/2m)^2 + o(p/2o)^2 >= 0

voilà, si je n'ai pas fait d'erreurs algébriques. Je ne sais pas comment vous pouvez simplifier l'expression résultante, donc cette solution pourrait être tout à fait gourmand en ressources, si vous allez vérifier de nombreux cercles/ellipses

oubliez la solution mathématique. Comme vous pouvez le voir facilement en dessinant, vous pouvez avoir jusqu'à quatre solutions, et donc probablement un polynôme de quatrième grade.

au Lieu de cela il suffit de faire une recherche binaire sur le bord de l'une des figures. Il est facile de déterminer si un point se trouve à l'intérieur d'une ellipse et encore plus dans un cercle (voir si la distance est plus courte que le rayon).

si vous voulez vraiment aller pour les maths, Wolfram MathWorld a un bel article ici: http://mathworld.wolfram.com/Circle-EllipseIntersection.html mais attention, vous devrez quand même écrire un résolveur d'équation polynomiale, probablement en utilisant quelque chose comme la recherche binaire.

Ce n'est pas compliqué. user168715 la réponse est généralement juste, mais faire le calcul n'est pas nécessaire. Juste la trigonométrie.

Trouver l'angle entre le centre des deux objets. En utilisant ceci vous pouvez trouver le point le plus proche du centre du cercle sur l'ellipse en utilisant la forme polaire:

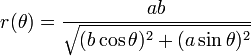
(extrait de L'article de Wikipedia sur Ellipses)

maintenant, comparez la distance entre les deux centres d'objet, en soustrayant le rayon de l'ellipse et du cercle.

peut-être que je manque quelque chose; peut-être ArcTan/Cos/Sin sont lents -- mais je ne le pense pas, et il devrait y avoir des approximations rapides si nécessaire.

je sais que c'est trop tard mais j'espère que ça aiderait quelqu'un. Mon approche pour résoudre ce problème était d'interpoler l'ellipse dans un polygone n-dimensions, puis de construire une ligne entre tous les 2 points et de trouver si le cercle croise avec l'une des lignes ou non. Cela ne fournit pas la meilleure performance, mais il est pratique et facile à mettre en œuvre.

Pour interpoler l'ellipse à un n-dimensions polygone, vous pouvez utiliser:

    float delta = (2 * PI) / n;

    std::vector<Point*> interpolation;

    for(float t = 0; t < (2 * PI); t += delta) {

        float x = rx * cos(t) + c->get_x();
        float y = ry * sin(t) + c->get_y();

        interpolation.push_back(new Point(x, y));
    }

c: le centre de la ellipse. RX: rayon de l'axe X de l'ellipse. ry: rayon de l'axe de l'ellipse aligné en Y.

maintenant nous avons les points d'interpolation, nous pouvons trouver l'intersection entre le cercle et les lignes entre tous les 2 points. Une façon de trouver la ligne-intersection de cricle est décrite ici, une intersection se produit si une intersection est produite entre les lignes et le cercle.

J'espère que cela aidera n'importe qui.

en Supposant: l'ellipse centrée à l'origine et avec le demi-grand axe (de longueur a) orienté le long de l'axe x, et avec un demi-mineur l'axe de longueur b; E2 est l'excentricité au carré, i.e. (a a-b b) / (a*a); le cercle est centré à X, Y et de rayon R.

les cas faciles sont: le centre du cercle est à l'intérieur de l'ellipse (i.e. hypot(X/A, Y/b) <= 1) il y a donc une intersection; le centre du cercle est à l'extérieur d'un cercle centré en 0 de rayon a+r (IE hypot (X,Y) > a+r) donc il n'y a pas d'intersection.

une approche pour les autres cas est de calculer la géodésie coordonnées (latitude, hauteur) du centre du cercle. Cercle coupe l'ellipse si et seulement si la hauteur est inférieure au rayon.

la latitude géodésique d'un point sur une ellipse est l'angle la normale à l'ellipse au point avec l'axe des x, et la hauteur d'un point à l'extérieur de l'ellipse est la distance de la point du point sur l'ellipse la plus proche. Note la latitude géodésique n'est pas la même que l'angle polaire du centre de l'ellipse au point à moins que l'ellipse est en fait circulaire.

dans les formules la conversion des coordonnées géodésiques lat, ht en coordonnées cartésiennes X, Y est X = (nu+ht) * cos (lat), Y = (nu * (1-E2) + ht) * sin(lat)) où nu = a / sqrt( 1-E2 * sin (lat) sin (lat)). Le point sur l'ellipse le plus proche de X, Y est le point avec la même latitude, mais la hauteur nulle, c'est à dire x = nu cos (lat), y = nu * (1-E2) * sin (lat). Notez que nu est une fonction de latitude.

malheureusement le processus de trouver lat, ht de X, Y est un itératif. Une approche consiste à trouver d'abord la latitude, puis hauteur.

un peu d'algèbre montre que la latitude satisfait lat = atan2( Y+ E2 * nu sin( lat), X) qui peut être utilisé pour calculer des approximations successives de la latitude, à partir de lat = atan2 (Y, X

Plus E2 est grande, c'est-à-dire plus l'ellipse est plate, plus itérations seront nécessaires. Par exemple, si l'ellipse est presque circulaire (dire E2<0.1) puis cinq itérations obtiendront x, y ci-dessous à l'intérieur de a*1e-12, mais si l'ellipse est très plate, par exemple E2=0,999 vous aurez besoin d'environ 300 itérations pour obtenir la même précision!