Comment convertir un point 3D en projection en perspective 2D?

je pense ce vont sans doute répondre à votre question. Voici ce que j'y ai écrit:

Voici une réponse très générale. Dites que la caméra est à (Xc, Yc, Zc) et que le point que vous voulez projeter est P = (X, Y, Z). La distance de la caméra au plan 2D sur lequel vous projetez est F (donc l'équation du plan est Z-Zc=F). Les coordonnées 2D de P projetées sur le plan sont (X', Y').

alors, très simplement:

X' = ((X - Xc) * (F/Z)) + Xc

Y' = ((Y - Yc) * (F/Z)) + Yc

si votre caméra est l'origine, alors cela simplifie à:

X' = X * (F/Z)

Y' = Y * (F/Z)

vous pouvez projeter 3D point en 2D en utilisant: Commons Math: the Apache Commons Mathematics Library avec seulement deux classes.

exemple pour Java Swing.

import org.apache.commons.math3.geometry.euclidean.threed.Plane;
import org.apache.commons.math3.geometry.euclidean.threed.Vector3D;


Plane planeX = new Plane(new Vector3D(1, 0, 0));
Plane planeY = new Plane(new Vector3D(0, 1, 0)); // Must be orthogonal plane of planeX

void drawPoint(Graphics2D g2, Vector3D v) {
    g2.drawLine(0, 0,
            (int) (world.unit * planeX.getOffset(v)),
            (int) (world.unit * planeY.getOffset(v)));
}

protected void paintComponent(Graphics g) {
    super.paintComponent(g);

    drawPoint(g2, new Vector3D(2, 1, 0));
    drawPoint(g2, new Vector3D(0, 2, 0));
    drawPoint(g2, new Vector3D(0, 0, 2));
    drawPoint(g2, new Vector3D(1, 1, 1));
}

Maintenant vous n'avez besoin de mettre à jour le planeX et planeY pour changer la perspective-projection, pour obtenir des choses comme ceci:

pour obtenir les coordonnées corrigées en perspective, divisez simplement par la coordonnée z :

xc = x / z
yc = y / z

cela fonctionne en supposant que la caméra est à (0, 0, 0) et que vous projetez sur le plan à z = 1 -- vous devez traduire les coordonnées relatives à la caméra autrement.

il y a quelques complications pour les courbes, dans la mesure où projeter les points D'une courbe de Bézier 3D ne vous donnera pas en général le même points comme tracer une courbe 2D Bezier à travers les points projetés.

Je ne sais pas à quel niveau vous posez cette question. Il semble que vous avez trouvé les formules en ligne, et essayez juste de comprendre ce qu'il fait. A la lecture de votre question, j'offre:

• Imaginez un rayon venant du spectateur (au point V) directement vers le centre du plan de projection (appelez-le C).
• Imaginez un second rayon du spectateur à un point de l'image (P) qui croise également le plan de projection à un certain point Q)
• le spectateur et les deux points d'intersection sur le plan de la vue forment un triangle (VCQ); les côtés sont les deux rayons et la ligne entre les points dans le plan.
• les formules utilisent ce triangle pour trouver les coordonnées de Q, Qui est où le pixel projeté ira

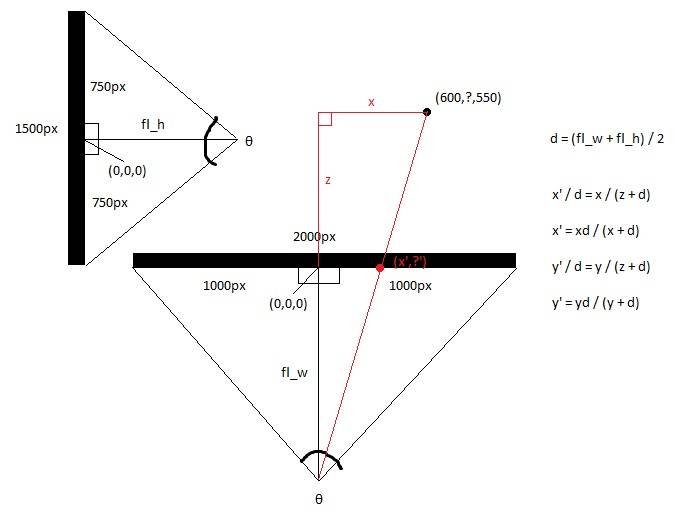
en regardant l'écran du haut, vous obtenez les axes x et Z.

en regardant l'écran de côté, vous obtenez les axes y et Z.

calculer les focales des vues supérieures et latérales, en utilisant la trigonométrie, qui est la distance entre l'oeil et le milieu de l'écran, qui est déterminée par le champ de vision de l'écran. Cela rend la forme de deux à droite les triangles dos à dos.

hw = screen_width / 2

hh = screen_height / 2

fl_top = HW/tan(θ / 2)

fl_side = HH / tan (θ/2)

Puis prendre la distance focale moyenne.

fl_ average = (fl_top + fl_side) / 2

Calculez maintenant le nouveau x et le nouveau y avec l'arithmétique de base, puisque le plus grand triangle droit fait à partir du point 3d et le point de l'oeil est congruent avec le plus petit triangle fait par le point 2d et le point de l'oeil.

x' = (x * fl_top) / (z + fl_top)

y' = (y * fl_top) / (z + fl_top)

Ou vous pouvez simplement définir

x' = x / (z + 1)

et

y' = y / (z + 1)

toutes les réponses répondent à la question posée dans le titre . Cependant, je voudrais ajouter une mise en garde qui est implicite dans le texte . Les patches Bézier sont utilisés pour représenter la surface, mais vous ne pouvez pas simplement transformer les points du patch et tesseler le patch en polygones, parce que cela résultera en une géométrie déformée. Vous pouvez, cependant, tesseler le patch d'abord dans les polygones en utilisant une tolérance d'écran transformée et puis transformez les polygones, ou vous pouvez convertir les patches Bézier en patches Bézier rationnels, puis tessellez ceux qui utilisent une tolérance écran-espace. Le premier est plus facile, mais le second est meilleur pour un système de production.

je pense que vous voulez la manière la plus facile. Pour cela, vous escaladeriez la tolérance de l'écran par la norme du Jacobien de la transformation de perspective inverse et utilisez cela pour déterminer la quantité de tessellation dont vous avez besoin dans l'espace modèle (il pourrait être plus facile de calculer le Jacobien d'avant, inverser cela, puis prendre la norme). Notez que cette norme dépend de la position, et vous voudrez peut-être l'évaluer à plusieurs endroits, selon la perspective. Rappelez-vous aussi que puisque la transformation projective est rationnelle, vous devez appliquer la règle du quotient pour calculer les dérivés.

je sais que c'est un vieux sujet mais votre illustration n'est pas correcte, le code source met en place la matrice de clip correcte.

[fov * aspectRatio][        0        ][        0              ][        0       ]
[        0        ][       fov       ][        0              ][        0       ]
[        0        ][        0        ][(far+near)/(far-near)  ][(2*near*far)/(near-far)]
[        0        ][        0        ][        1              ][        0       ]

quelque chose à ajouter à vos affaires:

cette matrice de clip ne fonctionne que si vous projetez sur un plan 2D statique si vous voulez ajouter le mouvement et la rotation de la caméra:

viewMatrix = clipMatrix * cameraTranslationMatrix4x4 * cameraRotationMatrix4x4;

permet de tourner le plan 2D et de le déplacer..-

Vous voulez déboguer votre système avec des sphères de déterminer si oui ou non vous avez un bon champ de vision. Si vous l'avez trop large, les sphères avec la déformation aux bords de l'écran dans des formes plus ovales pointées vers le centre du cadre. La solution à ce problème est de zoomer sur le cadre, en multipliant les coordonnées x et y pour le point tridimensionnel par un scalaire et ensuite rétrécir votre objet ou monde vers le bas par un facteur similaire. Ensuite, vous obtenez le beau rond droit sphère à travers la totalité de l'image.

je suis presque embarrassé qu'il m'ait fallu toute la journée pour comprendre celui-ci et j'étais presque convaincu qu'il y avait un mystérieux phénomène géométrique effrayant en cours ici qui exigeait une approche différente.

pourtant, on ne saurait surestimer l'importance de calibrer le coefficient zoom-cadre-de-vue par des sphères de rendu. Si vous ne savez pas où la "zone habitable" de votre univers, vous allez finir par marcher sur le soleil et la mise au rebut du projet. Vous voulez être en mesure de rendre une sphère n'importe où dans votre cadre de vue et l'avoir apparaître rond. Dans mon projet, l'unité sphère est massive par rapport à la région que je décris.

aussi, l'entrée obligatoire de wikipedia: Système De Coordonnées Sphériques

merci à @Mads Elvenheim pour un bon exemple de code. J'ai corrigé les petites erreurs de syntaxe dans le code (juste quelques problèmes const et des Opérateurs manquants évidents). En outre, près de et loin ont des significations très différentes dans vs.

pour votre plaisir, voici la version compilable (MSVC2013). Amuser. Attention, J'ai fait NEAR_Z et FAR_Z constant. Tu ne le veux probablement pas comme ça.

#include <vector>
#include <cmath>
#include <stdexcept>
#include <algorithm>

#define M_PI 3.14159

#define NEAR_Z 0.5
#define FAR_Z 2.5

struct Vector
{
    float x;
    float y;
    float z;
    float w;

    Vector() : x( 0 ), y( 0 ), z( 0 ), w( 1 ) {}
    Vector( float a, float b, float c ) : x( a ), y( b ), z( c ), w( 1 ) {}

    /* Assume proper operator overloads here, with vectors and scalars */
    float Length() const
    {
        return std::sqrt( x*x + y*y + z*z );
    }
    Vector& operator*=(float fac) noexcept
    {
        x *= fac;
        y *= fac;
        z *= fac;
        return *this;
    }
    Vector  operator*(float fac) const noexcept
    {
        return Vector(*this)*=fac;
    }
    Vector& operator/=(float div) noexcept
    {
        return operator*=(1/div);   // avoid divisions: they are much
                                    // more costly than multiplications
    }

    Vector Unit() const
    {
        const float epsilon = 1e-6;
        float mag = Length();
        if (mag < epsilon) {
            std::out_of_range e( "" );
            throw e;
        }
        return Vector(*this)/=mag;
    }
};

inline float Dot( const Vector& v1, const Vector& v2 )
{
    return v1.x*v2.x + v1.y*v2.y + v1.z*v2.z;
}

class Matrix
{
public:
    Matrix() : data( 16 )
    {
        Identity();
    }
    void Identity()
    {
        std::fill( data.begin(), data.end(), float( 0 ) );
        data[0] = data[5] = data[10] = data[15] = 1.0f;
    }
    float& operator[]( size_t index )
    {
        if (index >= 16) {
            std::out_of_range e( "" );
            throw e;
        }
        return data[index];
    }
    const float& operator[]( size_t index ) const
    {
        if (index >= 16) {
            std::out_of_range e( "" );
            throw e;
        }
        return data[index];
    }
    Matrix operator*( const Matrix& m ) const
    {
        Matrix dst;
        int col;
        for (int y = 0; y<4; ++y) {
            col = y * 4;
            for (int x = 0; x<4; ++x) {
                for (int i = 0; i<4; ++i) {
                    dst[x + col] += m[i + col] * data[x + i * 4];
                }
            }
        }
        return dst;
    }
    Matrix& operator*=( const Matrix& m )
    {
        *this = (*this) * m;
        return *this;
    }

    /* The interesting stuff */
    void SetupClipMatrix( float fov, float aspectRatio )
    {
        Identity();
        float f = 1.0f / std::tan( fov * 0.5f );
        data[0] = f*aspectRatio;
        data[5] = f;
        data[10] = (FAR_Z + NEAR_Z) / (FAR_Z- NEAR_Z);
        data[11] = 1.0f; /* this 'plugs' the old z into w */
        data[14] = (2.0f*NEAR_Z*FAR_Z) / (NEAR_Z - FAR_Z);
        data[15] = 0.0f;
    }

    std::vector<float> data;
};


inline Vector operator*( const Vector& v, Matrix& m )
{
    Vector dst;
    dst.x = v.x*m[0] + v.y*m[4] + v.z*m[8] + v.w*m[12];
    dst.y = v.x*m[1] + v.y*m[5] + v.z*m[9] + v.w*m[13];
    dst.z = v.x*m[2] + v.y*m[6] + v.z*m[10] + v.w*m[14];
    dst.w = v.x*m[3] + v.y*m[7] + v.z*m[11] + v.w*m[15];
    return dst;
}

typedef std::vector<Vector> VecArr;
VecArr ProjectAndClip( int width, int height, const VecArr& vertex )
{
    float halfWidth = (float)width * 0.5f;
    float halfHeight = (float)height * 0.5f;
    float aspect = (float)width / (float)height;
    Vector v;
    Matrix clipMatrix;
    VecArr dst;
    clipMatrix.SetupClipMatrix( 60.0f * (M_PI / 180.0f), aspect);
    /*  Here, after the perspective divide, you perform Sutherland-Hodgeman clipping
    by checking if the x, y and z components are inside the range of [-w, w].
    One checks each vector component seperately against each plane. Per-vertex
    data like colours, normals and texture coordinates need to be linearly
    interpolated for clipped edges to reflect the change. If the edge (v0,v1)
    is tested against the positive x plane, and v1 is outside, the interpolant
    becomes: (v1.x - w) / (v1.x - v0.x)
    I skip this stage all together to be brief.
    */
    for (VecArr::const_iterator i = vertex.begin(); i != vertex.end(); ++i) {
        v = (*i) * clipMatrix;
        v /= v.w; /* Don't get confused here. I assume the divide leaves v.w alone.*/
        dst.push_back( v );
    }

    /* TODO: Clipping here */

    for (VecArr::iterator i = dst.begin(); i != dst.end(); ++i) {
        i->x = (i->x * (float)width) / (2.0f * i->w) + halfWidth;
        i->y = (i->y * (float)height) / (2.0f * i->w) + halfHeight;
    }
    return dst;
}
#pragma once