Vous souhaitez utiliser le elliptique Arc commande. Malheureusement pour vous, cela vous oblige à spécifier les coordonnées cartésiennes (x, y) des points de début et de fin plutôt que les coordonnées polaires (rayon, angle) que vous avez, donc vous devez faire quelques calculs. Voici une fonction JavaScript qui devrait fonctionner (bien que je ne l'aie pas testée), et qui, j'espère, est assez explicite:

function polarToCartesian(centerX, centerY, radius, angleInDegrees) {
  var angleInRadians = angleInDegrees * Math.PI / 180.0;
  var x = centerX + radius * Math.cos(angleInRadians);
  var y = centerY + radius * Math.sin(angleInRadians);
  return [x,y];
}

Quels angles correspondent aux positions d'horloge qui dépendront de la coordonnée système; il suffit d'échanger et/ou d'annuler les Termes nas / cos si nécessaire.

La commande arc a les paramètres suivants:

rx, ry, x-axis-rotation, large-arc-flag, sweep-flag, x, y

Pour votre premier exemple:

rx=ry=25 et x-axis-rotation=0, puisque vous voulez un cercle et non une ellipse. Vous pouvez calculer à la fois les coordonnées de départ (que vous devriez Move to) et les coordonnées de fin (x, y) en utilisant la fonction ci-dessus, donnant (200, 175) et environ (182.322, 217.678), respectivement. Compte tenu de ces contraintes jusqu'à présent, il y a en fait quatre arcs qui pourraient être dessinés, de sorte que les deux drapeaux en sélectionnent un. Je suppose que vous voulez probablement dessiner un petit arc (ce qui signifie large-arc-flag = 0), dans le sens de l'angle décroissant (ce qui signifie sweep-flag = 0). Tous ensemble, le chemin SVG est:

M 200 175 A 25 25 0 0 0 182.322 217.678

Pour le deuxième exemple (en supposant que vous voulez dire aller dans la même direction, et donc un grand arc), le chemin SVG est:

M 200 175 A 25 25 0 1 0 217.678 217.678

Encore une fois, je ne les ai pas testés.

(edit 2016-06-01) si, comme @clocksmith, vous vous demandez pourquoi ils ont choisi cette API, jetez un oeil aux notes de mise en œuvre . Ils décrivent deux paramétrisations d'arc possibles, "paramétrisation de point final "(celle qu'ils ont choisie), et" paramétrisation de Centre " (qui est comme ce que la question utilise). Dans la description de "Endpoint parameterization", ils disent:

L'un des avantages du paramétrage des points de terminaison est qu'il permet une syntaxe de chemin cohérente dans laquelle toutes les commandes de chemin se terminent par les coordonnées du nouveau "courant point".

Donc, fondamentalement, c'est un effet secondaire des arcs étant considérés comme faisant partie d'un chemin plus large plutôt que de leur propre objet séparé. Je suppose que si votre moteur de rendu SVG est incomplet, il peut simplement ignorer tous les composants de chemin qu'il ne sait pas rendre, tant qu'il sait combien d'arguments ils prennent. Ou peut-être qu'il permet le rendu parallèle de différents morceaux d'un chemin avec de nombreux composants. Ou peut être qu'ils l'ont fait pour s'assurer que les erreurs d'arrondi ne s'accumulent pas sur toute la longueur d'un chemin complexe.

Les notes d'implémentation sont également utiles pour la question originale, car elles ont plus de pseudocode mathématique pour la conversion entre les deux paramétrisations(ce que je n'ai pas réalisé quand j'ai écrit cette réponse).

J'ai légèrement modifié la réponse de opsb et fait dans le remplissage de soutien pour le secteur du cercle. http://codepen.io/anon/pen/AkoGx

JS

function polarToCartesian(centerX, centerY, radius, angleInDegrees) {
  var angleInRadians = (angleInDegrees-90) * Math.PI / 180.0;

  return {
    x: centerX + (radius * Math.cos(angleInRadians)),
    y: centerY + (radius * Math.sin(angleInRadians))
  };
}

function describeArc(x, y, radius, startAngle, endAngle){

    var start = polarToCartesian(x, y, radius, endAngle);
    var end = polarToCartesian(x, y, radius, startAngle);

    var arcSweep = endAngle - startAngle <= 180 ? "0" : "1";

    var d = [
        "M", start.x, start.y, 
        "A", radius, radius, 0, arcSweep, 0, end.x, end.y,
        "L", x,y,
        "L", start.x, start.y
    ].join(" ");

    return d;       
}

document.getElementById("arc1").setAttribute("d", describeArc(200, 400, 100, 0, 220));

HTML

<svg>
  <path id="arc1" fill="orange" stroke="#446688" stroke-width="0" />
</svg>

Je voulais commenter la réponse de @ Ahtenus, en particulier sur le commentaire de Ray Hulha disant que le codepen ne montre aucun arc, Mais ma réputation n'est pas assez élevée.

La raison pour laquelle ce codepen ne fonctionne pas est que son html est défectueux avec une largeur de trait de zéro.

Je l'ai corrigé et ajouté un deuxième exemple ici : http://codepen.io/AnotherLinuxUser/pen/QEJmkN.

Le code html:

<svg>
    <path id="theSvgArc"/>
    <path id="theSvgArc2"/>
</svg>

Le CSS pertinent:

svg {
    width  : 500px;
    height : 500px;
}

path {
    stroke-width : 5;
    stroke       : lime;
    fill         : #151515;
}

Le javascript:

document.getElementById("theSvgArc").setAttribute("d", describeArc(150, 150, 100, 0, 180));
document.getElementById("theSvgArc2").setAttribute("d", describeArc(300, 150, 100, 45, 190));

Les réponses de @ opsb sont soignées, mais le point central n'est pas précis, d'ailleurs, comme l'a noté @Jithin, si l'angle est de 360, alors rien n'est dessiné du tout.

@Jithin a corrigé le problème 360, mais si vous avez sélectionné moins de 360 degrés, vous obtiendrez une ligne fermant la boucle d'arc, ce qui n'est pas nécessaire.

J'ai corrigé cela et ajouté de l'animation dans le code ci-dessous:

function myArc(cx, cy, radius, max){       
       var circle = document.getElementById("arc");
        var e = circle.getAttribute("d");
        var d = " M "+ (cx + radius) + " " + cy;
        var angle=0;
        window.timer = window.setInterval(
        function() {
            var radians= angle * (Math.PI / 180);  // convert degree to radians
            var x = cx + Math.cos(radians) * radius;  
            var y = cy + Math.sin(radians) * radius;
           
            d += " L "+x + " " + y;
            circle.setAttribute("d", d)
            if(angle==max)window.clearInterval(window.timer);
            angle++;
        }
      ,5)
 }     

  myArc(110, 110, 100, 360);
    

<svg xmlns="http://www.w3.org/2000/svg" style="width:220; height:220;"> 
    <path d="" id="arc" fill="none" stroke="red" stroke-width="2" />
</svg>

La fonction polartocartésienne originale de wdebeaum est correcte:

var angleInRadians = angleInDegrees * Math.PI / 180.0;

Inverser les points de début et de fin en utilisant:

var start = polarToCartesian(x, y, radius, endAngle);
var end = polarToCartesian(x, y, radius, startAngle);

Est déroutant (pour moi) car cela inversera le drapeau de balayage. Utilisation:

var start = polarToCartesian(x, y, radius, startAngle);
var end = polarToCartesian(x, y, radius, endAngle);

Avec le sweep-flag = " 0 "dessine des arcs" normaux " en contre-temps, je pense que c'est plus simple. Voir https://developer.mozilla.org/en-US/docs/Web/SVG/Tutorial/Paths

Une légère modification à la réponse de @opsb. Nous ne pouvons pas dessiner un cercle complet avec cette méthode. ie si nous donnons (0, 360) il ne sera pas dessiner quoi que ce soit. Donc, une légère modification faite pour résoudre ce problème. Il pourrait être utile d'afficher des résultats qui atteignent parfois 100%.

function polarToCartesian(centerX, centerY, radius, angleInDegrees) {
  var angleInRadians = (angleInDegrees-90) * Math.PI / 180.0;

  return {
    x: centerX + (radius * Math.cos(angleInRadians)),
    y: centerY + (radius * Math.sin(angleInRadians))
  };
}

function describeArc(x, y, radius, startAngle, endAngle){

    var endAngleOriginal = endAngle;
    if(endAngleOriginal - startAngle === 360){
        endAngle = 359;
    }

    var start = polarToCartesian(x, y, radius, endAngle);
    var end = polarToCartesian(x, y, radius, startAngle);

    var arcSweep = endAngle - startAngle <= 180 ? "0" : "1";

    if(endAngleOriginal - startAngle === 360){
        var d = [
              "M", start.x, start.y, 
              "A", radius, radius, 0, arcSweep, 0, end.x, end.y, "z"
        ].join(" ");
    }
    else{
      var d = [
          "M", start.x, start.y, 
          "A", radius, radius, 0, arcSweep, 0, end.x, end.y
      ].join(" ");
    }

    return d;       
}

document.getElementById("arc1").setAttribute("d", describeArc(120, 120, 100, 0, 359));

C'est une vieille question, mais j'ai trouvé le code utile et m'a sauvé trois minutes de réflexion :) donc j'ajoute une petite expansion à la réponse de @opsb.

Si vous voulez convertir cet arc en une tranche (pour permettre le remplissage), nous pouvons modifier légèrement le code:

function describeArc(x, y, radius, spread, startAngle, endAngle){
    var innerStart = polarToCartesian(x, y, radius, endAngle);
  	var innerEnd = polarToCartesian(x, y, radius, startAngle);
    var outerStart = polarToCartesian(x, y, radius + spread, endAngle);
    var outerEnd = polarToCartesian(x, y, radius + spread, startAngle);

    var largeArcFlag = endAngle - startAngle <= 180 ? "0" : "1";

    var d = [
        "M", outerStart.x, outerStart.y,
        "A", radius + spread, radius + spread, 0, largeArcFlag, 0, outerEnd.x, outerEnd.y,
        "L", innerEnd.x, innerEnd.y, 
        "A", radius, radius, 0, largeArcFlag, 1, innerStart.x, innerStart.y, 
        "L", outerStart.x, outerStart.y, "Z"
    ].join(" ");

    return d;
}

function polarToCartesian(centerX, centerY, radius, angleInDegrees) {
  var angleInRadians = (angleInDegrees-90) * Math.PI / 180.0;

  return {
    x: centerX + (radius * Math.cos(angleInRadians)),
    y: centerY + (radius * Math.sin(angleInRadians))
  };
}

var path = describeArc(150, 150, 50, 30, 0, 50)
document.getElementById("p").innerHTML = path
document.getElementById("path").setAttribute('d',path)

<p id="p">
</p>
<svg width="300" height="300" style="border:1px gray solid">
  <path id="path" fill="blue" stroke="cyan"></path>
</svg>

Et voilà!

Vous pouvez utiliser le code JSFiddle que j'ai fait pour la réponse ci-dessus:

Https://jsfiddle.net/tyw6nfee/

Tout ce que vous devez faire est de changer la console de dernière ligne.connectez le code et donnez-lui votre propre paramètre:

  console.log(describeArc(255,255,220,30,180));
  console.log(describeArc(CenterX,CenterY,Radius,startAngle,EndAngle))

Une image et du Python

Juste pour mieux clarifier et offrir une autre solution. Arc [A] commande, utiliser la position actuelle comme point de départ, donc vous devez utiliser Moveto [M] d'abord la commande.

Alors les paramètres de Arc sont les suivants:

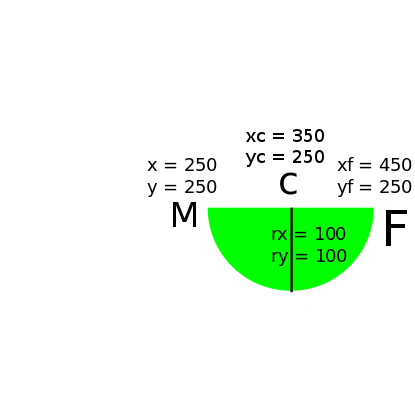
rx, ry, x-axis-rotation, large-arc-flag, sweep-flag, xf, yf

Si nous définissons par exemple le fichier svg suivant:

<svg width="5cm" height="5cm" viewBox="0 0 500 500"

xmlns="http://www.w3.org/2000/svg" version="1.1">

Le code suivant vous donnera ce résultat:

<g stroke="none" fill="lime">
<path d="
M 250 250
A 100 100 0 0 0 450 250
Z"/> 
</g>

Vous allez définir le point de départ avec M le point de fin avec les paramètres xf et yf de A.

Nous recherchons des cercles donc nous définissons rx égal à ry ce faisant fondamentalement maintenant il va essayer de trouver tout le cercle de rayon rx qui croisent le point de départ et de fin.

import numpy as np

def write_svgarc(xcenter,ycenter,r,startangle,endangle,output='arc.svg'):
    if startangle > endangle: 
        raise ValueError("startangle must be smaller than endangle")

    if endangle - startangle < 360:
        large_arc_flag = 0
        radiansconversion = np.pi/180.
        xstartpoint = xcenter + r*np.cos(startangle*radiansconversion)
        ystartpoint = ycenter - r*np.sin(startangle*radiansconversion)
        xendpoint = xcenter + r*np.cos(endangle*radiansconversion)
        yendpoint = ycenter - r*np.sin(endangle*radiansconversion)
        #If we want to plot angles larger than 180 degrees we need this
        if endangle - startangle > 180: large_arc_flag = 1
        with open(output,'a') as f:
            f.write(r"""<path d=" """)
            f.write("M %s %s" %(xstartpoint,ystartpoint))
            f.write("A %s %s 0 %s 0 %s %s" 
                    %(r,r,large_arc_flag,xendpoint,yendpoint))
            f.write("L %s %s" %(xcenter,ycenter))
            f.write(r"""Z"/>""" )

    else:
        with open(output,'a') as f:
            f.write(r"""<circle cx="%s" cy="%s" r="%s"/>"""
                    %(xcenter,ycenter,r))

, Vous pouvez avoir une explication plus détaillée dans ce post, que j'ai écrit.

Composant ReactJS basé sur la réponse sélectionnée:

import React from 'react';

const polarToCartesian = (centerX, centerY, radius, angleInDegrees) => {
    const angleInRadians = (angleInDegrees - 90) * Math.PI / 180.0;

    return {
        x: centerX + (radius * Math.cos(angleInRadians)),
        y: centerY + (radius * Math.sin(angleInRadians))
    };
};

const describeSlice = (x, y, radius, startAngle, endAngle) => {

    const start = polarToCartesian(x, y, radius, endAngle);
    const end = polarToCartesian(x, y, radius, startAngle);

    const largeArcFlag = endAngle - startAngle <= 180 ? "0" : "1";

    const d = [
        "M", 0, 0, start.x, start.y,
        "A", radius, radius, 0, largeArcFlag, 0, end.x, end.y
    ].join(" ");

    return d;
};

const path = (degrees = 90, radius = 10) => {
    return describeSlice(0, 0, radius, 0, degrees) + 'Z';
};

export const Arc = (props) => <svg xmlns="http://www.w3.org/2000/svg" viewBox="0 0 300 300">
    <g transform="translate(150,150)" stroke="#000" strokeWidth="2">
        <path d={path(props.degrees, props.radius)} fill="#333"/>
    </g>

</svg>;

export default Arc;

Version ES6:

const angleInRadians = angleInDegrees => (angleInDegrees - 90) * (Math.PI / 180.0);

const polarToCartesian = (centerX, centerY, radius, angleInDegrees) => {
    const a = angleInRadians(angleInDegrees);
    return {
        x: centerX + (radius * Math.cos(a)),
        y: centerY + (radius * Math.sin(a)),
    };
};

const arc = (x, y, radius, startAngle, endAngle) => {
    const fullCircle = endAngle - startAngle === 360;
    const start = polarToCartesian(x, y, radius, endAngle - 0.01);
    const end = polarToCartesian(x, y, radius, startAngle);
    const arcSweep = endAngle - startAngle <= 180 ? '0' : '1';

    const d = [
        'M', start.x, start.y,
        'A', radius, radius, 0, arcSweep, 0, end.x, end.y,
    ].join(' ');

    if (fullCircle) d.push('z');
    return d;
};