Comment calculer le nombre de paramètres du réseau neuronal convolutionnel?

J'utilise Lasagne pour créer un CNN pour l'ensemble de données MNIST. Je suis de près avec cet exemple: réseaux neuronaux convolutionnels et extraction de fonctionnalités avec Python .

L'architecture CNN que j'ai en ce moment, qui n'inclut pas de couches d'abandon, est: 

NeuralNet(
    layers=[('input', layers.InputLayer),        # Input Layer
            ('conv2d1', layers.Conv2DLayer),     # Convolutional Layer
            ('maxpool1', layers.MaxPool2DLayer), # 2D Max Pooling Layer
            ('conv2d2', layers.Conv2DLayer),     # Convolutional Layer
            ('maxpool2', layers.MaxPool2DLayer), # 2D Max Pooling Layer
            ('dense', layers.DenseLayer),        # Fully connected layer
            ('output', layers.DenseLayer),       # Output Layer
            ],
    # input layer
    input_shape=(None, 1, 28, 28),

    # layer conv2d1
    conv2d1_num_filters=32,
    conv2d1_filter_size=(5, 5),
    conv2d1_nonlinearity=lasagne.nonlinearities.rectify,

    # layer maxpool1
    maxpool1_pool_size=(2, 2),

    # layer conv2d2
    conv2d2_num_filters=32,
    conv2d2_filter_size=(3, 3),
    conv2d2_nonlinearity=lasagne.nonlinearities.rectify,

    # layer maxpool2
    maxpool2_pool_size=(2, 2),


    # Fully Connected Layer
    dense_num_units=256,
    dense_nonlinearity=lasagne.nonlinearities.rectify,

   # output Layer
    output_nonlinearity=lasagne.nonlinearities.softmax,
    output_num_units=10,

    # optimization method params
    update= momentum,
    update_learning_rate=0.01,
    update_momentum=0.9,
    max_epochs=10,
    verbose=1,
    )

cette couche produit les informations suivantes: 

  #  name      size
---  --------  --------
  0  input     1x28x28
  1  conv2d1   32x24x24
  2  maxpool1  32x12x12
  3  conv2d2   32x10x10
  4  maxpool2  32x5x5
  5  dense     256
  6  output    10

et produit le nombre de paramètres 217,706

je me demande comment ce nombre est calculé? J'ai lu un certain nombre de ressources, y compris la question de ce Empileur , mais aucune ne généralise clairement le calcul.

si possible, le calcul des paramètres d'apprentissage par couche peut-il être généralisé?

par exemple, couche de convolution: nombre de filtres x largeur du filtre x filtre de hauteur.

21
demandé sur nbro 2017-03-14 15:59:54

2 réponses

voyons d'abord comment le nombre de paramètres apprenables est calculé pour chaque type de couche que vous avez, puis calculez le nombre de paramètres dans votre exemple.

  • "Input layer : Tout ce que fait la couche input est de lire l'image input, il n'y a donc aucun paramètre que vous pourriez apprendre ici.

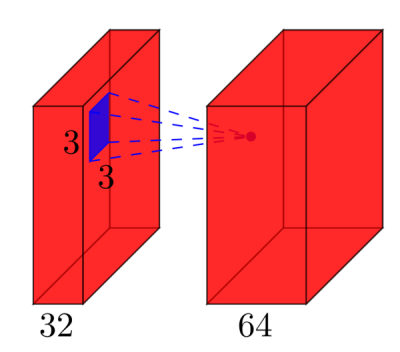
  • couches Convolutionnelles : considérer une couche convolutionnelle qui prend l cartes de traits à l'entrée, et a k cartes de traits comme sortie. La taille du filtre est n x m . Par exemple, cela ressemblera à ceci:

    Visualization of a convolutional layer

    ici, l'entrée a l=32 cartes de caractéristiques comme entrée, k=64 cartes de caractéristiques comme sortie, et la taille du filtre est n=3 x m=3 . Il est important de comprendre, que nous n'avons pas il suffit d'avoir un filtre 3x3, mais en fait un filtre 3x3x32, car notre entrée a 32 dimensions. Et nous apprenons 64 filtres 3x3x32 différents. Ainsi, le nombre total de poids est n*m*k*l . Ensuite, il y a aussi un terme de biais pour chaque carte de caractéristique, de sorte que nous avons un nombre total de paramètres de (n*m*l+1)*k .

  • Pooling layers : les couches de pooling font par exemple ce qui suit: "remplacer un voisinage 2x2 par sa valeur maximale". Donc, il n'y a pas de paramètre que vous pouvez apprendre dans une couche de mise en commun.
  • couches entièrement connectées : dans une couche entièrement connectée, toutes les unités d'entrée ont un poids distinct pour chaque unité de sortie. Pour les entrées n et les sorties m , le nombre de poids est n*m . En outre, vous avez un biais pour chaque noeud de sortie, de sorte que vous êtes à (n+1)*m paramètres.
  • couche de sortie : la couche de sortie est une couche normale couche entièrement connectée, donc (n+1)*m paramètres, où n est le nombre d'entrées et m est le nombre de sorties.

la dernière difficulté est la première couche entièrement connectée: nous ne connaissons pas la dimensionnalité de l'entrée de cette couche, car il s'agit d'une couche convolutionnelle. Pour le calculer, il faut commencer par la taille de l'image d'entrée, et calculer la taille de chaque couche convolutionnelle. Dans votre cas, Lasagne calcule déjà cela pour vous et les rapports les tailles - ce qui rend facile pour nous. Si vous devez calculer vous-même la taille de chaque couche, c'est un peu plus compliqué:

  • dans le cas le plus simple (comme votre exemple), la taille de la sortie d'une couche de convolution est input_size - (filter_size - 1) , dans votre cas: 28 - 4 = 24. Ceci est dû à la nature de la convolution: nous utilisons par exemple un voisinage 5x5 pour calculer un point - mais les deux lignes et colonnes les plus externes n'ont pas de 5x5 voisinage, donc nous ne pouvons pas calculer de production pour ces points. C'est pourquoi notre résultat est 2*2=4 lignes/colonnes plus petites que l'entrée.
  • si l'on ne veut pas que la sortie soit plus petite que l'entrée, on peut zéro-pad l'image (avec le paramètre pad de la couche convolutionnelle en Lasagne). E. g. si vous ajoutez 2 lignes/colonnes de zéros autour de l'image, la taille de sortie (28+4)-4=28. Ainsi, en cas de remplissage, la taille de sortie est input_size + 2*padding - (filter_size -1) .
  • si vous voulez explicitement réduire votre image pendant la convolution, vous pouvez définir un pas, par exemple stride=2 , ce qui signifie que vous déplacez le filtre par Pas de 2 pixels. Ensuite, l'expression devient ((input_size + 2*padding - filter_size)/stride) +1 .

dans votre cas, les calculs complets sont: 

  #  name                           size                 parameters
---  --------  -------------------------    ------------------------
  0  input                       1x28x28                           0
  1  conv2d1   (28-(5-1))=24 -> 32x24x24    (5*5*1+1)*32   =     832
  2  maxpool1                   32x12x12                           0
  3  conv2d2   (12-(3-1))=10 -> 32x10x10    (3*3*32+1)*32  =   9'248
  4  maxpool2                     32x5x5                           0
  5  dense                           256    (32*5*5+1)*256 = 205'056
  6  output                           10    (256+1)*10     =   2'570

donc dans votre réseau, vous avez un total de 832 + 9'248 + 205'056 + 2'570 = 217'706 paramètres d'apprentissage, ce qui est exactement ce que Lasagne rapport.

46
répondu hbaderts 2018-06-27 12:46:41

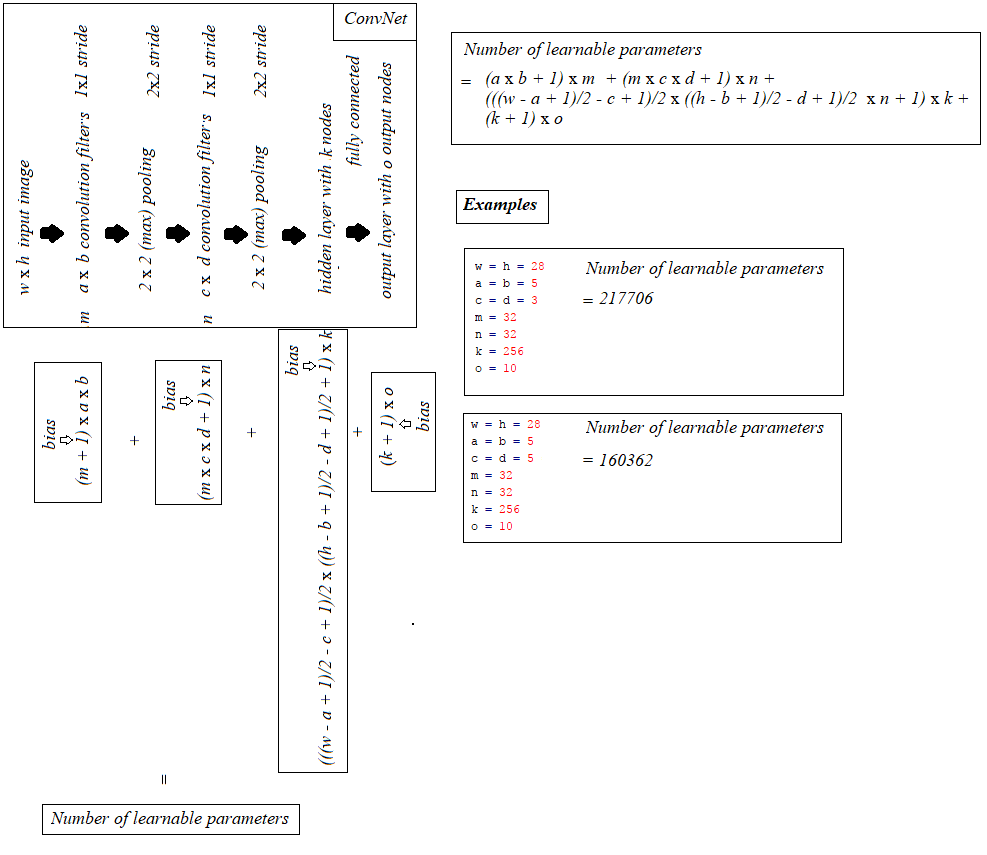
en s'appuyant sur l'excellente réponse de @hbaderts, je viens de trouver une formule pour un réseau I-C-P-C-P-H-O (puisque je travaillais sur un problème similaire), le partage dans la figure ci-dessous, peut être utile.

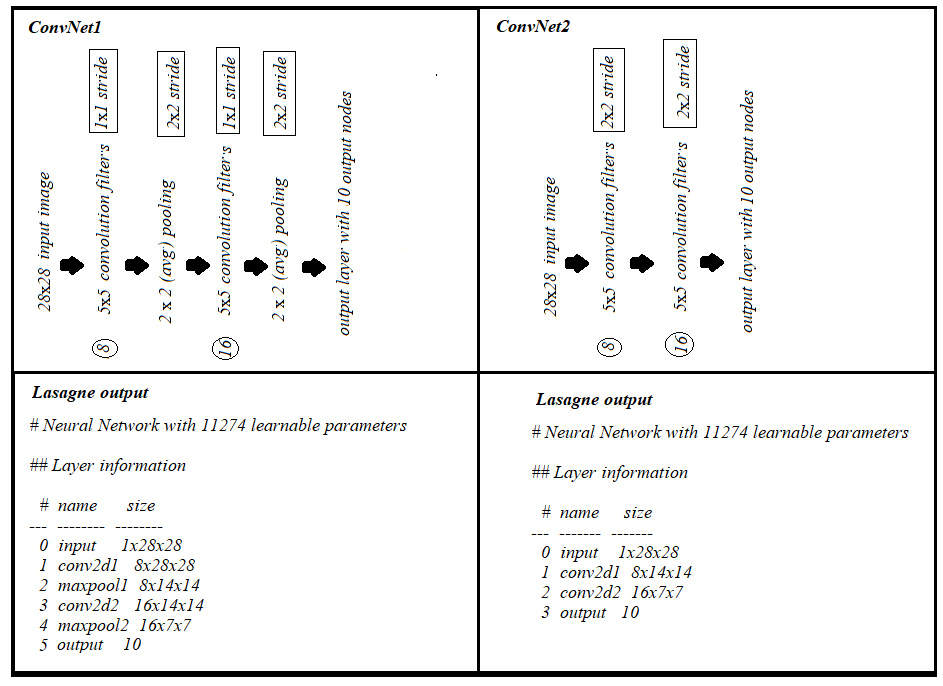
enter image description here

aussi, (1) couche de convolution avec 2x2 stride et (2) couche de convolution 1x1 stride + (max/avg) pooling avec 2x2 stride, chacun apporte les mêmes nombres de paramètres avec 'même' rembourrage, comme on peut le voir ci-dessous:

enter image description here

4
répondu Sandipan Dey 2017-08-11 07:13:09