Comment calculer l'angle entre une ligne et l'axe des abscisses?

Dans un langage de programmation (Python, C#, etc), je dois déterminer comment calculer l'angle entre une ligne et l'axe horizontal?

Je pense qu'une image décrit le mieux ce que je veux:

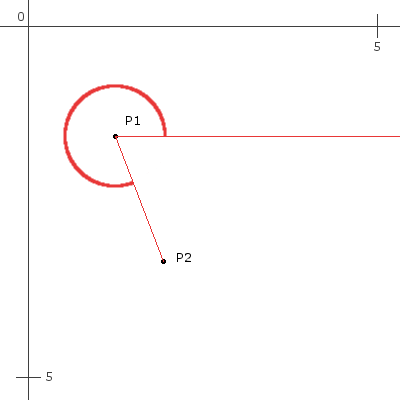
aucun mot ne peut décrire cette

Donnée (P1x,P1y) et (P2x,P2y) quelle est la meilleure façon de calculer cet angle? L'origine est dans le topleft et seul le quadrant positif est utilisé.

240
demandé sur Richard Howes 2011-09-28 19:58:40

7 réponses

Trouvez D'abord la différence entre le point de départ et le point final (ici, il s'agit plus d'un segment de ligne dirigé, pas d'une "ligne", puisque les lignes s'étendent à l'infini et ne commencent pas à un point particulier).

deltaY = P2_y - P1_y
deltaX = P2_x - P1_x

Calculez ensuite l'angle (qui va de l'axe X positif à {[4] } à l'axe Y positif à P1).

angleInDegrees = arctan(deltaY / deltaX) * 180 / PI

Mais arctan peut ne pas être idéal, car diviser les différences de cette façon effacera la distinction nécessaire pour distinguer quel quadrant l'angle est dans (voir ci-dessous). Utilisez plutôt ce qui suit si votre langue inclut une fonction atan2: 

angleInDegrees = atan2(deltaY, deltaX) * 180 / PI

Modifier (fév. 22, 2017): en général, cependant, appeler atan2(deltaY,deltaX) juste pour obtenir l'angle approprié pour cos et sin peut être inélégant. Dans ces cas, vous pouvez souvent faire ce qui suit:

  1. traitez (deltaX, deltaY) comme un vecteur.
  2. normalise ce vecteur en un vecteur unitaire. Pour ce faire, divisez deltaX et deltaY par la longueur du vecteur (sqrt(deltaX*deltaX+deltaY*deltaY)), sauf si la longueur est 0.
  3. après cela, {[12] } sera maintenant le cosinus de l'angle entre le vecteur et l'axe horizontal (dans la direction du X positif à l'axe Y positif à P1).
  4. et deltaY seront maintenant le sinus de cet angle.
  5. si la longueur du vecteur est 0, Il n'aura pas d'angle entre lui et l'axe horizontal (donc il n'aura pas de sinus et de cosinus significatifs).

Modifier (fév. 28, 2017): même sans normaliser (deltaX, deltaY):

  • le signe de {[12] } vous dira si le cosinus décrit à l'étape 3 est positif ou négatif.
  • le signe de deltaY vous indiquera si le sinus décrit à l'étape 4 est positif ou négatif.
  • les signes de deltaX et deltaY vous indiqueront dans quel quadrant se trouve l'angle, par rapport à l'axe X positif à P1:
    • +deltaX, +deltaY: 0 à 90 degrés.
    • -deltaX, +deltaY: 90 à 180 degrés.
    • -deltaX, -deltaY: 180 à 270 degrés (-180 à -90 degrés).
    • +deltaX, -deltaY: 270 à 360 degrés (-90 à 0 degrés).

Une implémentation en Python utilisant des radians (fournie le 19 juillet 2015 par Eric Leschinski, qui a édité ma réponse):

from math import *
def angle_trunc(a):
    while a < 0.0:
        a += pi * 2
    return a

def getAngleBetweenPoints(x_orig, y_orig, x_landmark, y_landmark):
    deltaY = y_landmark - y_orig
    deltaX = x_landmark - x_orig
    return angle_trunc(atan2(deltaY, deltaX))

angle = getAngleBetweenPoints(5, 2, 1,4)
assert angle >= 0, "angle must be >= 0"
angle = getAngleBetweenPoints(1, 1, 2, 1)
assert angle == 0, "expecting angle to be 0"
angle = getAngleBetweenPoints(2, 1, 1, 1)
assert abs(pi - angle) <= 0.01, "expecting angle to be pi, it is: " + str(angle)
angle = getAngleBetweenPoints(2, 1, 2, 3)
assert abs(angle - pi/2) <= 0.01, "expecting angle to be pi/2, it is: " + str(angle)
angle = getAngleBetweenPoints(2, 1, 2, 0)
assert abs(angle - (pi+pi/2)) <= 0.01, "expecting angle to be pi+pi/2, it is: " + str(angle)
angle = getAngleBetweenPoints(1, 1, 2, 2)
assert abs(angle - (pi/4)) <= 0.01, "expecting angle to be pi/4, it is: " + str(angle)
angle = getAngleBetweenPoints(-1, -1, -2, -2)
assert abs(angle - (pi+pi/4)) <= 0.01, "expecting angle to be pi+pi/4, it is: " + str(angle)
angle = getAngleBetweenPoints(-1, -1, -1, 2)
assert abs(angle - (pi/2)) <= 0.01, "expecting angle to be pi/2, it is: " + str(angle)

Tous les tests passent. Voir https://en.wikipedia.org/wiki/Unit_circle

379
répondu Peter O. 2017-02-28 11:21:34

Désolé, mais je suis sûr que la réponse de Peter est fausse. Notez que l'axe y descend de la page (commun dans les graphiques). En tant que tel, le calcul de deltaY doit être inversé, ou vous obtenez la mauvaise réponse.

Considérez: 

System.out.println (Math.toDegrees(Math.atan2(1,1)));
System.out.println (Math.toDegrees(Math.atan2(-1,1)));
System.out.println (Math.toDegrees(Math.atan2(1,-1)));
System.out.println (Math.toDegrees(Math.atan2(-1,-1)));

Donne

45.0
-45.0
135.0
-135.0

Donc, si dans l'exemple ci-dessus, P1 est (1,1) et P2 est (2,2) [parce que Y augmente en bas de la page], le code ci-dessus donnera 45,0 degrés pour l'exemple montré, ce qui est faux. Changez l'ordre du calcul de deltaY et cela fonctionne correctement.

48
répondu user1641082 2013-07-13 00:24:51

J'ai trouvé une solution en Python qui fonctionne bien !

from math import atan2,degrees

def GetAngleOfLineBetweenTwoPoints(p1, p2):
    return degrees(atan2(p2 - p1, 1))

print GetAngleOfLineBetweenTwoPoints(1,3)
1
répondu dctremblay 2015-10-06 07:09:41

Compte tenu de la question exacte, nous mettant dans un système de coordonnées "spécial" où l'axe positif signifie Descendre (comme un écran ou une vue d'interface), vous devez adapter cette fonction comme ceci, et négatif les coordonnées Y:

Exemple dans Swift 2.0

func angle_between_two_points(pa:CGPoint,pb:CGPoint)->Double{
    let deltaY:Double = (Double(-pb.y) - Double(-pa.y))
    let deltaX:Double = (Double(pb.x) - Double(pa.x))
    var a = atan2(deltaY,deltaX)
    while a < 0.0 {
        a = a + M_PI*2
    }
    return a
}

Cette fonction donne une réponse correcte à la question. La réponse est en radians, donc l'utilisation, pour voir les angles en degrés, Est: 

let p1 = CGPoint(x: 1.5, y: 2) //estimated coords of p1 in question
let p2 = CGPoint(x: 2, y : 3) //estimated coords of p2 in question

print(angle_between_two_points(p1, pb: p2) / (M_PI/180))
//returns 296.56
1
répondu philippe 2016-06-11 13:32:12

Basé sur la référence "Peter O".. Voici la version java 

private static final float angleBetweenPoints(PointF a, PointF b) {
float deltaY = b.y - a.y;
float deltaX = b.x - a.x;
return (float) (Math.atan2(deltaY, deltaX)); }
0
répondu Venkateswara Rao 2015-10-14 03:15:51 
deltaY = Math.Abs(P2.y - P1.y);
deltaX = Math.Abs(P2.x - P1.x);

angleInDegrees = Math.atan2(deltaY, deltaX) * 180 / PI

if(p2.y > p1.y) // Second point is lower than first, angle goes down (180-360)
{
  if(p2.x < p1.x)//Second point is to the left of first (180-270)
    angleInDegrees += 180;
  else (270-360)
    angleInDegrees += 270;
}
else if (p2.x < p1.x) //Second point is top left of first (90-180)
  angleInDegrees += 90;
0
répondu mamashare 2017-02-07 10:53:22

Fonction Matlab: 

function [lineAngle] = getLineAngle(x1, y1, x2, y2) 
    deltaY = y2 - y1;
    deltaX = x2 - x1;

    lineAngle = rad2deg(atan2(deltaY, deltaX));

    if deltaY < 0
        lineAngle = lineAngle + 360;
    end
end
0
répondu Benas 2017-03-26 13:08:48