Comment calculer l'angle de rotation à partir de points rectangles?
j'ai 4 points 1,2,3,4 qui ferme un rectangle.
Les points sont dans une gamme dans ce de la manière suivante: x1y1x2y2x3y3x4y4
Le problème que j'ai est que le rectangle peut être tourné dans un angle.
Comment puis-je calculer les points d'origine (contour gris), et l'angle?
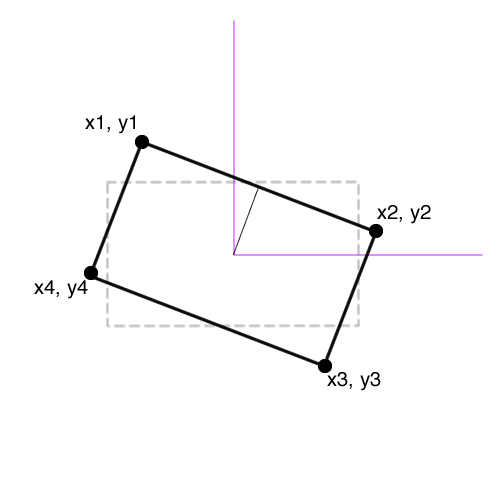
j'essaie de reproduire ceci effet en javascript+CSS3-transform, donc je dois d'abord connaître les dimensions droites et ensuite tourner avec le css.
je voudrais juste savoir si le rectangle est droit en comparant les points par exemple,y1==y2
if(x1==x4 && x2==x3 && y1==y2 && y4==y3){
rectangle.style.top = y1;
rectangle.style.left = x1;
rectangle.style.width = x2-x1;
rectangle.style.height = y4-y1;
rectangle.style.transform = "rotate(?deg)";
}
3 réponses
Vous pouvez utiliser n'importe quelle paire de coordonnées sur le même côté de calculer l'angle de rotation. Notez que les angles mathématiques supposent normalement 0 aussi longtemps que l'axe +ve X et augmentent par rotation dans le sens antihoraire (donc le long de l'axe +ve Y est de 90°, -l'axe de ve X est de 180° et ainsi de suite).
de plus, les fonctions de trigonométrie javascript renvoient des valeurs en radians qui doivent être converties en degrés avant d'être utilisées dans une transformation CSS.
Si la forme n'est pas tourné plus de 90°, alors la vie est assez simple et vous pouvez utiliser le rapport tanget d'un triangle angle droit:
tan(angle) = length of opposite side / length of adjacent side
pour L'OP, les meilleurs coins à utiliser sont 1 et 4 de sorte que la rotation est maintenue dans le premier quadrant et dans le sens des aiguilles d'une montre (selon le projet CSS3 spec). En termes javascript:
var rotationRadians = Math.atan((x1 - x4) / (y1 - y4));
Pour convertir en degrés:
var RAD2DEG = 180 / Math.PI;
var rotationDegrees = rotationRadians * RAD2DEG;
si la rotation est supérieure à 90°, vous devrez ajuster l'angle. par exemple lorsque l'angle est supérieur à 90°, mais moins de 180°, vous obtiendrez un -ve résultat de la ci-dessus et avez besoin d'ajouter 180°:
rotationDegrees += 180;
aussi, si vous utilisez les dimensions de la page, les coordonnées y augmentent en descendant la page, ce qui est le contraire du sens mathématique normal donc vous devez inverser le sens de y1 - y4 dans ce qui précède.
Modifier
basé sur l'orientation des points dans L'OP, ce qui suit est une fonction générale pour retourner le centre et dans le sens des aiguilles d'une montre du rectangle en degrés. C'est tout ce que vous devez savoir, si vous pouvez faire pivoter les coins à "niveau" si vous le souhaitez. Vous pouvez appliquer des fonctions trigonométriques pour calculer de nouveaux Coins ou juste faire quelques moyennes (similaire à la réponse de Ian).
/* General case solution for a rectangle
*
* Given coordinages of [x1, y1, x2, y2, x3, y3, x4, y4]
* where the corners are:
* top left : x1, y1
* top right : x2, y2
* bottom right: x3, y3
* bottom left : x4, y4
*
* The centre is the average top left and bottom right coords:
* center: (x1 + x3) / 2 and (y1 + y3) / 2
*
* Clockwise rotation: Math.atan((x1 - x4)/(y1 - y4)) with
* adjustment for the quadrant the angle is in.
*
* Note that if using page coordinates, y is +ve down the page which
* is the reverse of the mathematic sense so y page coordinages
* should be multiplied by -1 before being given to the function.
* (e.g. a page y of 400 should be -400).
*/
function getRotation(coords) {
// Get center as average of top left and bottom right
var center = [(coords[0] + coords[4]) / 2,
(coords[1] + coords[5]) / 2];
// Get differences top left minus bottom left
var diffs = [coords[0] - coords[6], coords[1] - coords[7]];
// Get rotation in degrees
var rotation = Math.atan(diffs[0]/diffs[1]) * 180 / Math.PI;
// Adjust for 2nd & 3rd quadrants, i.e. diff y is -ve.
if (diffs[1] < 0) {
rotation += 180;
// Adjust for 4th quadrant
// i.e. diff x is -ve, diff y is +ve
} else if (diffs[0] < 0) {
rotation += 360;
}
// return array of [[centerX, centerY], rotation];
return [center, rotation];
}
le centre du rectangle est juste entre deux coins opposés:
cx = (x1 + x3) / 2
cy = (y1 + y3) / 2
La taille du rectangle est la distance entre deux points:
w = sqrt(pow(x2-x1, 2) + pow(y2-y1, 2))
h = sqrt(pow(x3-x2, 2) + pow(y3-y2, 2))
les coins du rectangle gris peuvent être calculés à partir du Centre et de la taille, par exemple le coin supérieur gauche:
x = cx - w / 2
y = cy - h / 2
l'angle est l'arctangent d'un côté du carré:
a = arctan2(y4 - y1, x4 - x1)
(Je ne suis pas sûr exactement quel angle il retourne, ou quel angle vous attendez pour cela matière, donc vous avez à tester un peu.)
Euh, mathématiques de collège?
var deg = 90 - Math.arctan((x2-x1) / (y2-y1));
voici comment on obtient l'angle entre la ligne rose verticale et la ligne noire à partir de l'intersection de la ligne rose.
Les dimensions peuvent être calculées à l'aide du théorème de Pythagore:
var width = Math.sqrt((x2-x1)^2 / (y2-y1)^2));
var height = Math.sqrt((x1-x4)^2) / (y4-y1)^2));
les coordonnées de position (à gauche et en haut) sont les moyennes de x1 et x3 et y1 et y3 respectivement.
var left = Math.floor((x1 + x3) / 2);
var top = Math.floor((y1 + y3) / 2);
vous voulez utiliser le truc de la marge négative.
var marginLeft = -Math.ceil(width / 2);
var marginTop = -Math.ceil(height / 2);