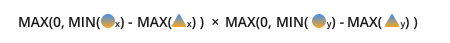Combien deux rectangles se chevauchent-ils?

La formule d'intersection sera

SI= Max(0, Min(XA2, XB2) - Max(XA1, XB1)) * Max(0, Min(YA2, YB2) - Max(YA1, YB1))

, Puis l'union sera S=SA+SB-SI

Et enfin, le rapport sera SI / S.

J'ai récemment rencontré ce problème et j'ai appliqué la réponse D'Yves, mais d'une manière ou d'une autre cela a conduit à la mauvaise taille de la zone, alors je l'ai réécrite.

En supposant deux rectangles A et B, découvrez combien ils se chevauchent et si oui, renvoyez la taille de la zone:

IF A.right < B.left OR A.left > B.right
    OR A.bottom < B.top OR A.top > B.bottom THEN RETURN 0

width := IF A.right > B.right THEN B.right - A.left ELSE A.right - B.left
height := IF A.bottom > B.bottom THEN B.bottom - A.top ELSE A.bottom - B.top

RETURN width * height

En supposant que le rectangle doit être parallèle à l'axe x et y car cela semble être la situation des commentaires et des réponses précédents.

Je ne peux pas encore poster de commentaire, mais je voudrais souligner que les deux réponses précédentes semblent ignorer le cas où un rectangle latéral est totalement dans le côté de l'autre rectangle. Veuillez me corriger si je me trompe.

Considérez le cas

a: (1,1), (4,4)
b: (2,2), (5,3)

Dans ce cas, nous voyons que pour l'intersection, la hauteur doit être bTop - bBottom parce que la partie verticale de b est entièrement contenu dans a.

Nous avons juste besoin d'ajouter plus de cas comme suit :( le code peut être court-circuité si vous traitez top et bottom comme la même chose que right et left, de sorte que vous n'avez pas besoin de dupliquer le morceau conditionnel deux fois, mais cela devrait faire.)

if aRight <= bLeft or bRight <= aLeft or aTop <= bBottom or bTop <= aBottom:
    # There is no intersection in these cases
    return 0
else:
    # There is some intersection

    if aRight >= bRight and aLeft <= bLeft:
        # From x axis point of view, b is wholly contained in a
        width = bRight - bLeft
    elif bRight >= aRight and bLeft <= aLeft:
        # From x axis point of view, a is wholly contained in b
        width = aRight - aLeft
    elif aRight >= bRight:
        width = bRight - aLeft
    else:
        width = aRight - bLeft

    if aTop >= bTop and aBottom <= bBottom:
        # From y axis point of view, b is wholly contained in a
        height = bTop - bBottom
    elif bTop >= aTop and bBottom <= aBottom:
        # From y axis point of view, a is wholly contained in b
        height = aTop - aBottom
    elif aTop >= bTop:
        height = bTop - aBottom
    else:
        height = aTop - bBottom

return width * height

Juste corriger les réponses précédentes pour que le rapport soit compris entre 0 et 1 (en utilisant Python):

    # (x1,y1) top-left coord, (x2,y2) bottom-right coord, (w,h) size
    A = {'x1': 0, 'y1': 0, 'x2': 99, 'y2': 99, 'w': 100, 'h': 100}
    B = {'x1': 0, 'y1': 0, 'x2': 49, 'y2': 49, 'w':  50, 'h':  50}

    # overlap between A and B
    SA = A['w']*A['h']
    SB = B['w']*B['h']
    SI = np.max([ 0, 1 + np.min([A['x2'],B['x2']]) - np.max([A['x1'],B['x1']]) ]) * np.max([ 0, 1 + np.min([A['y2'],B['y2']]) - np.max([A['y1'],B['y1']]) ])
    SU = SA + SB - SI
    overlap_AB = float(SI) / float(SU)
    print 'overlap between A and B: %f' % overlap_AB

    # overlap between A and A
    B = A
    SB = B['w']*B['h']
    SI = np.max([ 0, 1 + np.min([A['x2'],B['x2']]) - np.max([A['x1'],B['x1']]) ]) * np.max([ 0, 1 + np.min([A['y2'],B['y2']]) - np.max([A['y1'],B['y1']]) ])
    SU = SA + SB - SI
    overlap_AA = float(SI) / float(SU)
    print 'overlap between A and A: %f' % overlap_AA

La sortie sera:

    overlap between A and B: 0.250000
    overlap between A and A: 1.000000

[ymin_a, xmin_a, ymax_a, xmax_a] = list(bbox_a)
[ymin_b, xmin_b, ymax_b, xmax_b] = list(bbox_b)

x_intersection = min(xmax_a, xmax_b) - max(xmin_a, xmin_b) + 1
y_intersection = min(ymax_a, ymax_b) - max(ymin_a, ymin_b) + 1

if x_intersection <= 0 or y_intersection <= 0:
    return 0
else:
    return x_intersection * y_intersection

@User3025064 est correct et est la solution la plus simple, cependant, l'exclusivité doit être vérifiée d'abord pour les rectangles qui ne se croisent pas, par exemple, pour les rectangles A & B (en Visual Basic):

If A.Top =< B.Bottom or A.Bottom => B.Top or A.Right =< B.Left or A.Left => B.Right then
    Exit sub   'No intersection
else
    width = ABS(Min(XA2, XB2) - Max(XA1, XB1))
    height = ABS(Min(YA2, YB2) - Max(YA1, YB1))
    Area = width * height      'Total intersection area.
End if

La réponse de @user3025064 est la bonne réponse. La réponse acceptée retourne par inadvertance les appels Max et MIN internes. Nous n'avons pas non plus besoin de vérifier d'abord si elles se croisent ou non si nous utilisons la formule présentée, MAX (0, x) par opposition à ABS(x). S'ils ne se croisent pas, MAX (0, x) renvoie zéro ce qui rend la zone d'intersection 0 (c'est-à-dire disjointe).

Je suggère que @ Yves Daoust corrige sa réponse car c'est celle acceptée qui apparaît à quiconque cherche ce problème. Lorsque encore une fois, voici la bonne formule pour l'intersection:

SI = Max(0, Min(XA2, XB2) - Max(XA1, XB1)) * Max(0, Min(YA2, YB2) - Max(YA1, YB1))

Le reste comme d'habitude. Union:

SU = SA + SB - SI

Et ratio:

SI/SU

Bien que la réponse acceptée donnée soit correcte, je pense qu'il vaut la peine d'explorer cette réponse d'une manière qui rendra la justification de la réponse complètement évidente. C'est trop commun d'un algorithme pour avoir une réponse incomplète (ou pire, controversée). En outre, avec seulement un coup d'œil passant à la formule donnée, vous risquez de manquer la beauté, l'extensibilité et les décisions qui sont prises.

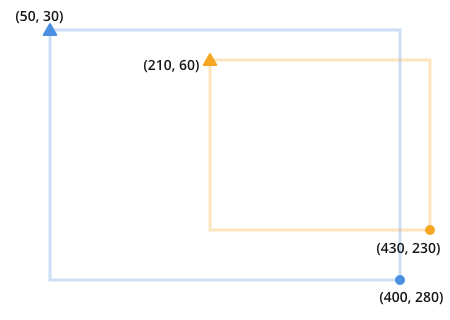
Tout d'abord, considérons une façon de définir une boîte à deux dimensions est avec:

• (x, y) pour le point supérieur gauche
• (x, y) pour le point inférieur droit

Cela pourrait ressembler à:

J'indique le coin supérieur gauche avec un triangle et le coin inférieur droit avec un cercle. C'est pour éviter la syntaxe opaque comme x1, x2 pour cet exemple.

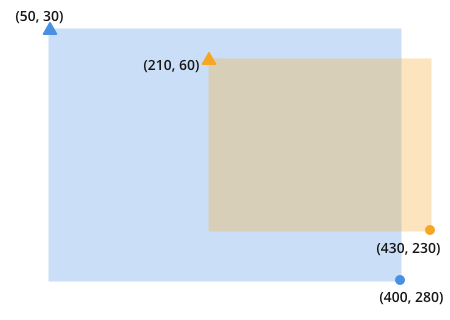
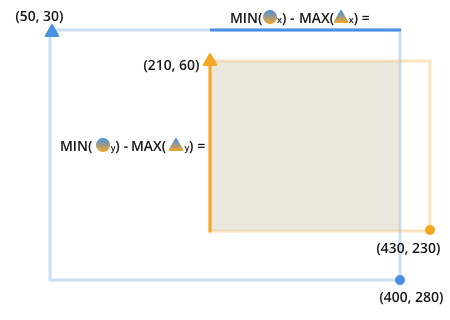
Deux rectangles qui se chevauchent peuvent ressembler à ceci:

Notez que pour trouver le chevauchement, vous cherchez l'endroit où l'orange et le bleu entrer en collision:

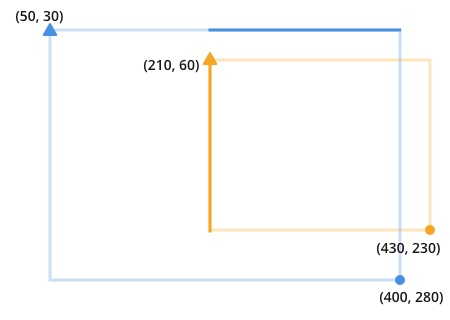
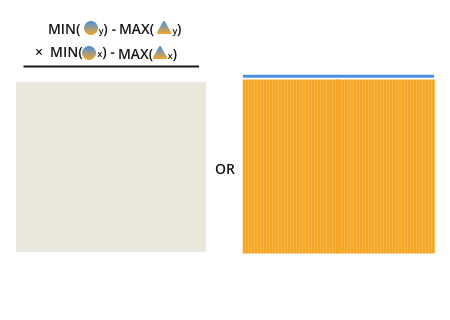
Une fois que vous reconnaissez cela, il devient évident que le chevauchement est le résultat de trouver et de multiplier ces deux lignes obscures:

La longueur de chaque ligne est la valeur minimale du point de cercle entre les lignes que nous voulons comparer, moins la valeur maximale des points triangulaires.

En d'autres termes, la longueur de la ligne qui peut s'adapter sur les deux lignes que nous sommes la comparaison est faite en soustrayant le point le plus proche du côté le plus long de la ligne du point le plus éloigné du côté le plus proche de la ligne.

Trouver ces lignes donne des informations complètes sur les zones qui se chevauchent.

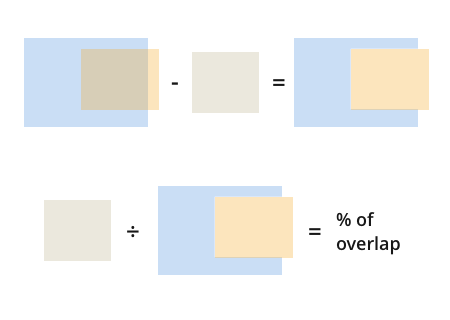
Une fois que vous avez ceci, trouver le pourcentage de chevauchement est trivial:

Mais attendez, si le rectangle orange ne se chevauche pas avec le bleu alors vous allez avoir un problème:

Avec cet exemple, vous obtenez un -850 pour notre zone de chevauchement, cela ne peut pas être juste. Pire encore, si une détection ne chevauche aucune dimension (ni sur l'axe x ni sur l'axe y), vous obtiendrez toujours un nombre positif car Les deux dimensions sont négatives. C'est pourquoi vous voyez le Max(0, ...) * Max(0, ...) dans le cadre de la solution; cela garantit que si l'un des chevauchements est négatif, vous obtiendrez un 0 de votre fonction.

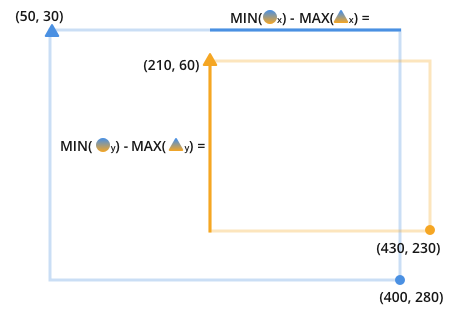
La formule finale dans en accord avec notre symbologie:

Il est à noter que l'utilisation de la fonction max(0, ...) peut ne pas être nécessaire. Vous voudrez peut-être savoir si quelque chose chevauche l'une de ses dimensions plutôt que toutes; Si vous utilisez max, vous effacerez cette information. Pour cette raison, considérez comment vous voulez traiter les images qui ne se chevauchent pas. Normalement, la fonction max est très bien à utiliser, mais cela vaut la peine d'être conscient de ce qu'elle fait.

Enfin, remarquez que depuis cette comparaison ne concerne que les mesures linéaires, il peut être mis à l'échelle à des dimensions arbitraires ou quadrilatères qui se chevauchent arbitraires.

Pour résumer:

intersecting_area = 
max(0, min(orange.circle.x, blue.circle.x) - max(orange.triangle.x, blue.triangle.x)) * max(0, min(orange.circle.y, blue_circle.y) - max(orange.triangle.y, blue.triangle.y))

percent_coverage = intersecting_area / (orange_area + blue_area - intersecting_area)