En quoi un arbre de dépassement de goulot d'étranglement minimum est-il différent d'un arbre de dépassement minimum?
Un arbre couvrant de goulot d'étranglement minimum d'un graphe pondéré G est un arbre couvrant de G tel que minimise le poids maximum de n'importe quel bord dans l'arbre couvrant. Un MBST n'est pas nécessairement un MST (minimum spanning tree).
Veuillez donner un exemple où ces déclarations ont du sens.
2 réponses
Regardez l'exemple MST sur Wikipedia pour référence:
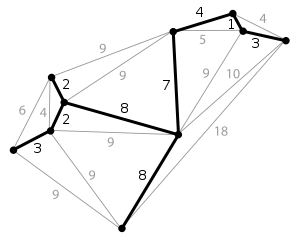
Un goulot d'étranglement dans un arbre spanning est un bord de poids maximum dans cet arbre. Il peut y avoir plusieurs goulots d'étranglement (tous du même poids bien sûr) dans un arbre couvrant. Dans le Wikipedia MST il y a deux goulots d'étranglement de poids 8.
Maintenant, prenez un arbre couvrant minimum d'un graphique donné (il peut y avoir plusieurs MSTs, tous avec le même poids total de bord bien sûr) et appelez le poids maximum de bord B. Dans notre exemple B = 8.
Tout arbre couvrant qui a également un goulot d'étranglement de B = 8 est un MBST. Mais ce n'est peut - être pas un MST (parce que le poids total du bord est plus grand que le meilleur possible).
Alors, prenez le Wikipedia MST et modifiez-le (ajoutez / supprimez quelques bords) de sorte que
- Il reste un arbre couvrant, et
- Il n'utilise toujours pas de poids > 8, encore
- Vous augmentez le poids total des bords
Par exemple, modifiez simplement le sous-arbre "à gauche" du Wikipedia MST (composé de poids {2, 2, 3}) à {2, 3, 6}, augmentant ainsi le poids total des bords de 4 sans changer le goulot d'étranglement de 8. Bingo, vous avez créé un MBST qui n'est pas un MST.
Avant de répondre à votre question, permettez-moi de définir certains des termes utilisés ici...
1), Spanning Tree : arbre recouvrant d'un graphe est un arbre qui couvre tous les sommets de ce graphe.
2) minimum spanning tree (MST): MST d'un graphe donné est un arbre couvrant dont la longueur est minimale parmi tous les arbres couvrant possibles de ce graphe. Plus clairement, pour un graphique donné, énumérez tous les arbres couvrant possibles (qui peuvent être très grands) et choisissez celui dont la somme de poids de bord est minimum.
3) Bottleneck minimum spanning tree (MBST): MBST d'un graphe donné est un arbre couvrant dont le poids maximum de bord est minimum parmi tous les arbres couvrant possibles. Plus clairement, pour un graphique donné, énumérez tous les arbres couvrant possibles et le poids maximal des arêtes pour chacun des arbres couvrant. Parmi ceux-ci, choisissez l'arbre couvrant dont le poids maximal du bord est minimum.
Maintenant, regardons l'image suivante avec un nœud quatre graphique...
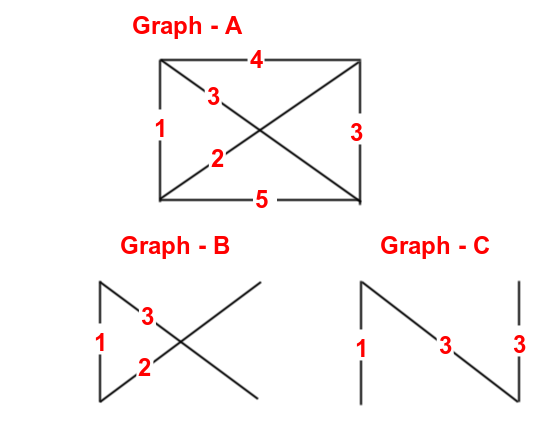
Graph-A est le graphe d'origine donné. Si je liste tous les arbres couvrant possibles pour ce graphique et que je choisis celui dont la somme des poids des arêtes est minimale, alors j'obtiendrai le graphique-B. Donc, Graph-B est L'Arbre de répartition Minimum (MST). Notez que son poids total est 1+2+3 = 6.
Maintenant, si je choisis un arbre couvrant dont le poids maximum de bord est minimum (C'est-à-dire MBST), alors je peux finir par ramasser Graph-B (ou) Graph-C. notez que ces deux arbres couvrant ont poids maximum de bord 3, qui est minimum parmi tous les arbres couvrant possibles.
À partir des Graph-B et Graph-C, il est clair que même si le Graph-C est un MBST, ce N'est pas MST. Parce que son poids total est 1+3+3=7, ce qui est supérieur au poids total de MST dessiné dans le graphique-B (c'est-à-dire 6).
Donc MBST n'est pas nécessairement un MST d'un graphique donné. Mais le MST doit être MBST.