Comment ajuster une courbe sinusoïdale à mes données avec pylab et numpy?
pour un projet scolaire, j'essaie de montrer que les économies suivent un schéma de croissance relativement sinusoïdal. Au-delà de l'économie de l'informatique, qui est certes douteuse, je construis une simulation python pour montrer que même si nous laissons un certain degré d'aléatoire s'installer, nous pouvons toujours produire quelque chose de relativement sinusoïdal. Je suis content de mes données que je produis mais maintenant J'aime trouver un moyen d'obtenir un graphique sinusoïdal qui correspond assez étroitement aux données. Je sais que tu peux faire un ajustement polynomial, mais pouvez-vous faire sinusoïdale de la forme?
Merci pour votre aide à l'avance. Dites-moi s'il y a des parties du code que vous voulez voir.
4 réponses
Vous pouvez utiliser le optimisation des moindres carrés fonction en scipy pour ajuster n'importe quelle fonction arbitraire à une autre. Dans le cas de l'ajustement d'une fonction sin, les 3 paramètres à ajuster sont l'offset ('a'), l'amplitude ('b') et la phase ('c').
tant Que vous faire une première estimation des paramètres, l'optimisation doit converger.Heureusement pour une fonction sinusoïdale, les premières estimations de 2 d'entre eux sont faciles: l'offset peut être estimé en prenant la moyenne de la données et l'amplitude via le RMS (3 * Écart type / rqrt (2)).
Note: lors d'une édition ultérieure, un ajustement de fréquence a également été ajouté. Cela ne fonctionne pas très bien (peut mener à de très pauvres). Ainsi, l'utilisation à votre discrétion, mon conseil serait de ne pas utiliser ajustement de fréquence à moins que l'erreur de fréquence est inférieure à quelques pour cent.
Ce qui conduit à le code suivant:
import numpy as np
from scipy.optimize import leastsq
import pylab as plt
N = 1000 # number of data points
t = np.linspace(0, 4*np.pi, N)
f = 1.15247 # Optional!! Advised not to use
data = 3.0*np.sin(f*t+0.001) + 0.5 + np.random.randn(N) # create artificial data with noise
guess_mean = np.mean(data)
guess_std = 3*np.std(data)/(2**0.5)/(2**0.5)
guess_phase = 0
guess_freq = 1
guess_amp = 1
# we'll use this to plot our first estimate. This might already be good enough for you
data_first_guess = guess_std*np.sin(t+guess_phase) + guess_mean
# Define the function to optimize, in this case, we want to minimize the difference
# between the actual data and our "guessed" parameters
optimize_func = lambda x: x[0]*np.sin(x[1]*t+x[2]) + x[3] - data
est_amp, est_freq, est_phase, est_mean = leastsq(optimize_func, [guess_amp, guess_freq, guess_phase, guess_mean])[0]
# recreate the fitted curve using the optimized parameters
data_fit = est_amp*np.sin(est_freq*t+est_phase) + est_mean
# recreate the fitted curve using the optimized parameters
fine_t = np.arange(0,max(t),0.1)
data_fit=est_amp*np.sin(est_freq*fine_t+est_phase)+est_mean
plt.plot(t, data, '.')
plt.plot(t, data_first_guess, label='first guess')
plt.plot(fine_t, data_fit, label='after fitting')
plt.legend()
plt.show()
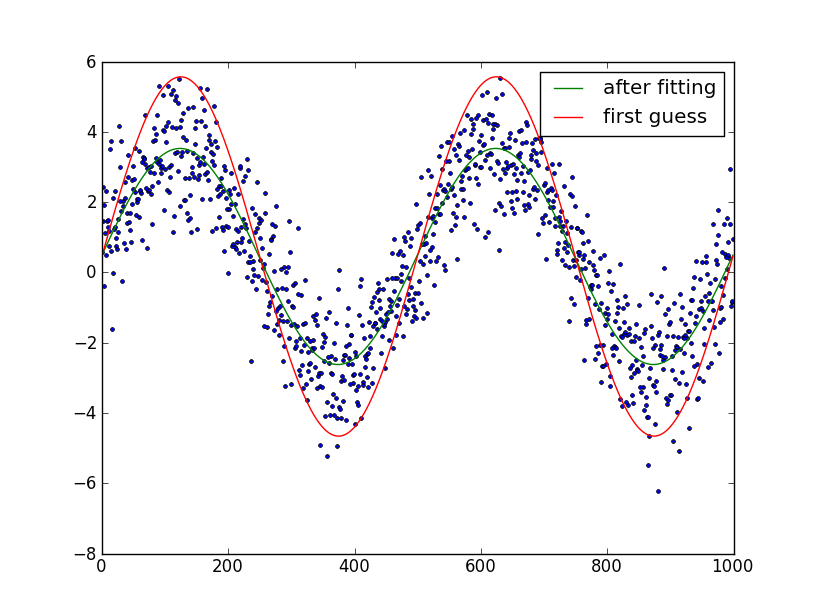
Edit: je suppose que vous connaissez le numéro des périodes de l'onde sinusoïdale. Si ce n'est pas le cas, c'est plus délicat. Vous pouvez essayer de deviner le nombre de périodes par traçage manuel et essayer de l'optimiser comme votre 6ème paramètre.
Voici une fonction d'ajustement sans paramètre fit_sin() cela ne nécessite pas de deviner manuellement la fréquence:
import numpy, scipy.optimize
def fit_sin(tt, yy):
'''Fit sin to the input time sequence, and return fitting parameters "amp", "omega", "phase", "offset", "freq", "period" and "fitfunc"'''
tt = numpy.array(tt)
yy = numpy.array(yy)
ff = numpy.fft.fftfreq(len(tt), (tt[1]-tt[0])) # assume uniform spacing
Fyy = abs(numpy.fft.fft(yy))
guess_freq = abs(ff[numpy.argmax(Fyy[1:])+1]) # excluding the zero frequency "peak", which is related to offset
guess_amp = numpy.std(yy) * 2.**0.5
guess_offset = numpy.mean(yy)
guess = numpy.array([guess_amp, 2.*numpy.pi*guess_freq, 0., guess_offset])
def sinfunc(t, A, w, p, c): return A * numpy.sin(w*t + p) + c
popt, pcov = scipy.optimize.curve_fit(sinfunc, tt, yy, p0=guess)
A, w, p, c = popt
f = w/(2.*numpy.pi)
fitfunc = lambda t: A * numpy.sin(w*t + p) + c
return {"amp": A, "omega": w, "phase": p, "offset": c, "freq": f, "period": 1./f, "fitfunc": fitfunc, "maxcov": numpy.max(pcov), "rawres": (guess,popt,pcov)}
l'estimation initiale de la fréquence est donnée par la fréquence de crête dans le domaine de fréquence en utilisant FFT. Le résultat d'ajustement est presque parfait s'il n'y a qu'une seule fréquence dominante (autre que le pic de fréquence zéro).
import pylab as plt
N, amp, omega, phase, offset, noise = 500, 1., 2., .5, 4., 3
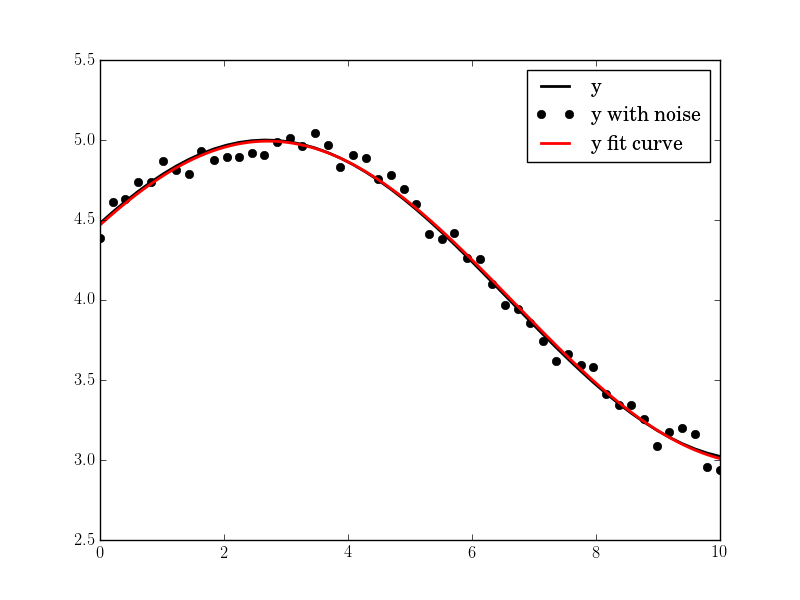
#N, amp, omega, phase, offset, noise = 50, 1., .4, .5, 4., .2
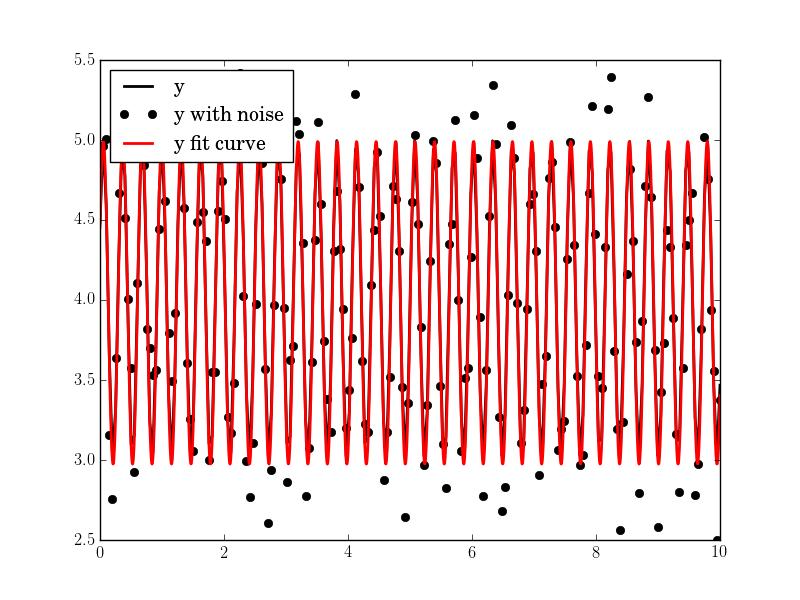
#N, amp, omega, phase, offset, noise = 200, 1., 20, .5, 4., 1
tt = numpy.linspace(0, 10, N)
tt2 = numpy.linspace(0, 10, 10*N)
yy = amp*numpy.sin(omega*tt + phase) + offset
yynoise = yy + noise*(numpy.random.random(len(tt))-0.5)
res = fit_sin(tt, yynoise)
print( "Amplitude=%(amp)s, Angular freq.=%(omega)s, phase=%(phase)s, offset=%(offset)s, Max. Cov.=%(maxcov)s" % res )
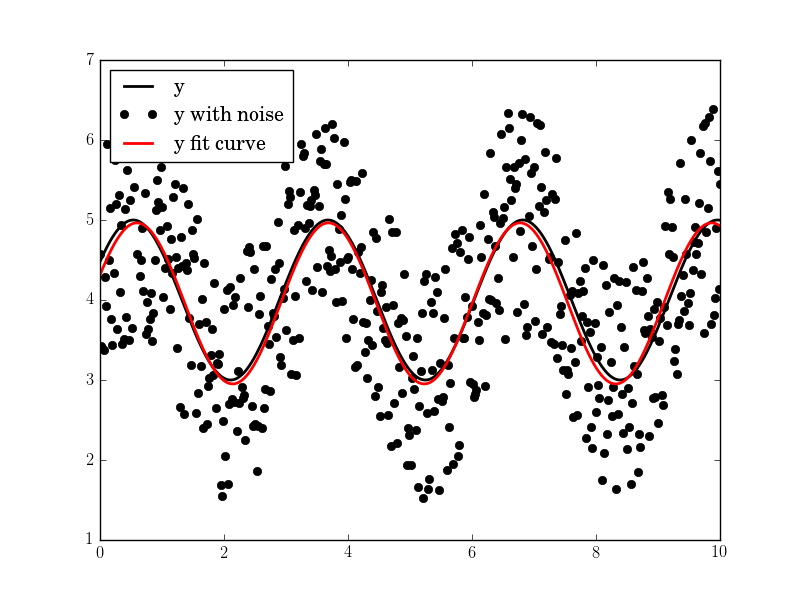
plt.plot(tt, yy, "-k", label="y", linewidth=2)
plt.plot(tt, yynoise, "ok", label="y with noise")
plt.plot(tt2, res["fitfunc"](tt2), "r-", label="y fit curve", linewidth=2)
plt.legend(loc="best")
plt.show()
Le résultat est bon, même avec le haut de bruit:
Amplitude=1.00660540618, Angulaire freq.= 2.03370472482, phase=0.360276844224, offset=3.95747467506, Max. Cov.= 0,0122923578658
plus conviviale pour nous est la fonction curvefit. Voici un exemple:
import numpy as np
from scipy.optimize import curve_fit
import pylab as plt
N = 1000 # number of data points
t = np.linspace(0, 4*np.pi, N)
data = 3.0*np.sin(t+0.001) + 0.5 + np.random.randn(N) # create artificial data with noise
guess_freq = 1
guess_amplitude = 3*np.std(data)/(2**0.5)
guess_phase = 0
guess_offset = np.mean(data)
p0=[guess_freq, guess_amplitude,
guess_phase, guess_offset]
# create the function we want to fit
def my_sin(x, freq, amplitude, phase, offset):
return np.sin(x * freq + phase) * amplitude + offset
# now do the fit
fit = curve_fit(my_sin, t, data, p0=p0)
# we'll use this to plot our first estimate. This might already be good enough for you
data_first_guess = my_sin(t, *p0)
# recreate the fitted curve using the optimized parameters
data_fit = my_sin(t, *fit[0])
plt.plot(data, '.')
plt.plot(data_fit, label='after fitting')
plt.plot(data_first_guess, label='first guess')
plt.legend()
plt.show()
les méthodes actuelles pour ajuster une courbe de sin à un ensemble de données donné nécessitent une première estimation des paramètres, suivie d'un processus d'inter-génération. Il s'agit d'un problème de régression non linéaire.
Dans le cas de la fonction y = a + r*sin(w*x+phi) ou y=a+b*sin(w*x)+c*cos(w*x), Voir pages 35-36 du document "Régression sinusoidale" publié sur Scribd
Dans le cas de la fonction y = a + p*x + r*sin(w*x+phi) : pages 49 à 51 du chapitre "linéaire Mixte et sinusoïdale régressions".
Dans le cas de fonctions plus complexes, le processus général est expliqué dans le chapitre "Generalized sinusoidal regression" pages 54-61, suivi d'un exemple numérique y = r*sin(w*x+phi)+(b/x)+c*ln(x), pages 62-63