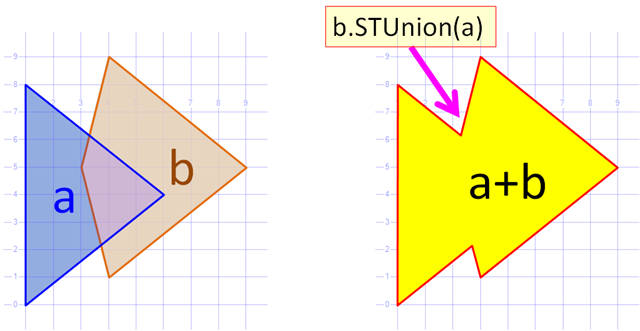
Comment combiner des polygones complexes?

C'est une très bonne question. J'ai implémenté le même algorithme sur c# il y a quelque temps. L'algorithme construit un contour commun de deux polygones (i.e. construit une union sans trous). Elle est ici.

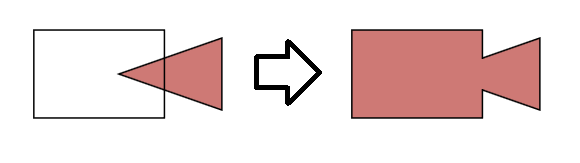
Étape 1. Créer graphique qui décrit les polygones.

entrée: premier polygone (n points), deuxième polygone (m points). Sortie: graphique. Vertex-point de polygone point d'intersection.

nous devrions trouver des intersections. Itérer sur tous les côtés du polygone, dans les deux polygones [O(n*m)] et trouver toutes les intersections.

• si une intersection n'est pas trouvée, il suffit d'ajouter des sommets et de les relier pour le bord.

• si des intersections sont trouvées, les Trier par longueur à leur point de départ, ajouter tous Vertex (start, end et intersections) et connect (déjà en l'ordre de tri) du bord.

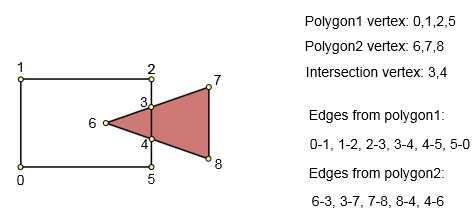
Étape 2. Contrôle graphique construit

si nous n'avons trouvé aucun point d'intersection lors de la construction du graphe, nous avons l'une des conditions suivantes:

1. Polygon1 contient polygon2 - retour polygon1
2. Polygon2 contient polygon1 - retour polygon2
3. Polygon1 et polygon2 ne se croisent pas. Renvoie polygon1 et polygon2.

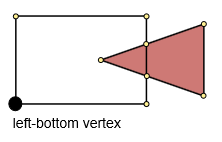
Étape 3. Trouve le vertex du bas gauche.

trouver les coordonnées minimales x et y (minx, miny). Trouvez ensuite la distance minimale entre (minx, miny) et les points du polygone. Ce point sera le point en bas à gauche.

Étape 4. Construire un contour commun.

nous commençons à traverser le graphique à partir de la gauche-en bas et continuer jusqu'à nous revenir. Au début, nous marque tous bords non visités. À chaque itération, vous devez sélectionner le point suivant et de le marquer comme visité.

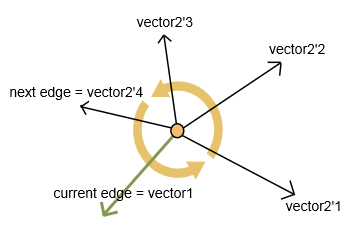
pour choisir le point suivant, choisissez un bord avec un angle interne maximal dans le sens contraire des aiguilles d'une montre.

Je calcule deux vecteurs: vector1 pour le bord courant et vector2 pour chaque bord non-visité suivant (tel que présenté sur la photo).

pour les vecteurs Je calcule:

1. produit Scalaire (produit scalaire). Elle renvoie une valeur liée à un angle entre les vecteurs.
2. produit vecteur (produit croisé). Elle renvoie un nouveau vecteur. Si z-coordonnée de ceci vecteur positif, produit scalaire me donne angle droit dans sens anti-horaire. Else( la coordonnée z est négative), I calculer l'angle entre les vecteurs 360 angle de scalaire produit.

en conséquence j'obtiens un bord (et un vertex correspondant) avec l'angle maximum.

j'ajoute à la liste de résultats chaque vertex passé. La liste des résultats est le polygone de l'union.

Remarques

1. cet algorithme nous permet de fusionner plusieurs polygones-pour appliquer itérativement avec les paires de polygones.
2. si vous avez un chemin qui se compose de nombreuses courbes de Bézier et les lignes, vous devriez aplatir ce chemin d'abord.

Vous devez déterminer les points qui se trouvent à l'intérieur . Après avoir enlevé ces points, vous pouvez insérer un ensemble de points "extérieurs" dans l'autre. Vos points d'insertion (par exemple, où vous avez la flèche dans l'image à droite) sont là où vous avez dû supprimer des points des ensembles d'entrée.

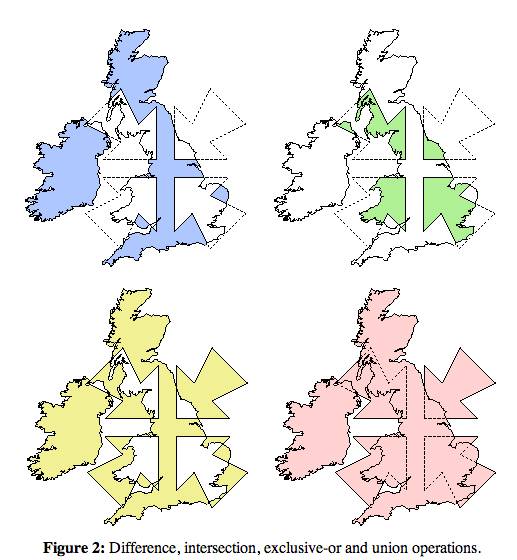
C'est un sujet difficile mais bien compris, qui va souvent sous le nom "opérations booléennes régularisées sur les polygones." Vous pourriez regarder ce MathOverflow réponse , qui comprend la figure ci-dessous (à partir de Alan Murta de l'écrêtage de la bibliothèque ), avec The pink union, les OP's combinent :

bonne question! Je n'ai jamais essayé cela avant, mais je vais prendre une fissure à elle maintenant.

tout d'abord: vous devez savoir où ces deux formes se chevauchent. Pour ce faire, vous pouvez regarder chaque bord dans le polygone a et voir où il se croise et bord dans le polygone B. Dans cet exemple, il devrait y avoir deux points d'intersection.

puis: faire la forme de l'union. Vous pouvez prendre tous les deux sommets A et B, et aussi les points d'intersection, puis d'exclure les sommets contenus par la forme finale. Pour trouver ces points, il semble que vous pourriez juste trouver n'importe quel vertex de A qui est à l'intérieur de B, et n'importe quel Vertex de B qui est à L'intérieur de A.

Essayer gpc .

une solution que j'ai vu en utilisant des arbres BSP est décrite ici .

essentiellement, il décrit l'intersection en termes d'une union des bords du polygone A qui sont à l'intérieur du polygone B (y compris les bords partiels, et calculé à l'aide d'un arbre BSP ). Ensuite, vous pouvez définir Un / B ~ (~ Un /\ ~ B ), où ~ dénote une inversion de l'enroulement du polygone, / dénote une union et /\ dénote une intersection.

en regroupant des pays, j'espère qu'il n'y aura pas de chevauchement -- vous pourriez prendre un algorithme assez naïf qui cherche des vertices partagés - une vue simple serait d'itérer à travers les points sur un polygone, voir si c'est sur l'un de vos autres polygones, et partage le même point suivant ou Précédent pour voir s'il y a une correspondance. Ensuite, il suffit de supprimer le vertex partagé pour créer votre union

j'avais besoin de résoudre ce même problème aujourd'hui et j'ai trouvé la solution avec ce lib: http://www.cs.man.ac.uk / ~toby / alan/ software / .

il a beaucoup d'implémentations de langage la liste ici y compris Java, Obj-C, C#, Lua, python et plus.

c'est une très vieille question mais Union_ fonction de Boost a fonctionné pour moi.

voir cet extrait ci-dessous:

#include <iostream>
#include <vector>

#include <boost/geometry.hpp>
#include <boost/geometry/geometries/point_xy.hpp>
#include <boost/geometry/geometries/polygon.hpp>

#include <boost/foreach.hpp>


int main()
{
    typedef boost::geometry::model::polygon<boost::geometry::model::d2::point_xy<double> > polygon;

    polygon green, blue;

    boost::geometry::read_wkt(
        "POLYGON((0 0, 0 10, 10 10, 10 0, 0 0))", green);

    boost::geometry::read_wkt(
        "POLYGON((5 5, 5 15, 15 15, 15 5, 5 5))", blue);

    std::vector<polygon> output;
    boost::geometry::union_(green, blue, output);

    int i = 0;
    std::cout << "green || blue:" << std::endl;
    BOOST_FOREACH(polygon const& p, output)
    {
        std::cout << i++ << ": " << boost::geometry::area(p) << std::endl;

        for (int i = 0; i < p.outer().size(); i++)
        {
            std::cout << p.outer().at(i).x() << " " << p.outer().at(i).y() << std::endl;
        }
    }



    return 0;
}