Comment calculer la distance euclidienne avec NumPy?

il y a une fonction pour ça en principe. Ça s'appelle euclidienne .

exemple:

from scipy.spatial import distance
a = (1, 2, 3)
b = (4, 5, 6)
dst = distance.euclidean(a, b)

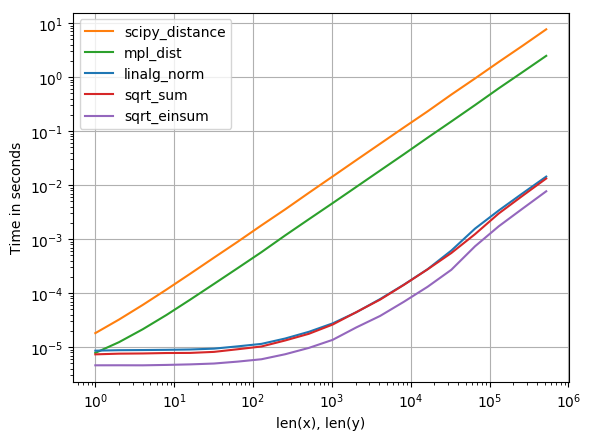
pour quiconque s'intéresse au calcul de distances multiples à la fois, j'ai fait une petite comparaison en utilisant perfplot (un petit projet de la mine). Il s'avère que

a_min_b = a - b
numpy.sqrt(numpy.einsum('ij,ij->i', a_min_b, a_min_b))

calcule les distances des lignes de a et b les plus rapides. Cela vaut également pour une seule rangée!

Code pour reproduire le tracé:

import matplotlib
import numpy
import perfplot
from scipy.spatial import distance


def linalg_norm(data):
    a, b = data
    return numpy.linalg.norm(a-b, axis=1)


def sqrt_sum(data):
    a, b = data
    return numpy.sqrt(numpy.sum((a-b)**2, axis=1))


def scipy_distance(data):
    a, b = data
    return list(map(distance.euclidean, a, b))


def mpl_dist(data):
    a, b = data
    return list(map(matplotlib.mlab.dist, a, b))


def sqrt_einsum(data):
    a, b = data
    a_min_b = a - b
    return numpy.sqrt(numpy.einsum('ij,ij->i', a_min_b, a_min_b))


perfplot.show(
    setup=lambda n: numpy.random.rand(2, n, 3),
    n_range=[2**k for k in range(20)],
    kernels=[linalg_norm, scipy_distance, mpl_dist, sqrt_sum, sqrt_einsum],
    logx=True,
    logy=True,
    xlabel='len(x), len(y)'
    )

un Autre exemple de ce problème méthode de résolution :

def dist(x,y):   
    return numpy.sqrt(numpy.sum((x-y)**2))

a = numpy.array((xa,ya,za))
b = numpy.array((xb,yb,zb))
dist_a_b = dist(a,b)

je veux expliquer sur la réponse simple avec diverses notes de performance. np.linalg.norm fera peut-être plus que ce dont vous avez besoin:

dist = numpy.linalg.norm(a-b)

premièrement - cette fonction est conçue pour travailler sur une liste et retourner toutes les valeurs, p.ex. pour comparer la distance de pA à l'ensemble des points sP :

sP = set(points)
pA = point
distances = np.linalg.norm(sP - pA, ord=2, axis=1.)  # 'distances' is a list

rappelez-vous plusieurs choses:

• les appels de fonctions Python sont coûteux.
• [régulier] Python ne cache pas les recherches de noms.

Donc

def distance(pointA, pointB):
    dist = np.linalg.norm(pointA - pointB)
    return dist

n'est pas aussi innocent qu'il en a l'air.

>>> dis.dis(distance)
  2           0 LOAD_GLOBAL              0 (np)
              2 LOAD_ATTR                1 (linalg)
              4 LOAD_ATTR                2 (norm)
              6 LOAD_FAST                0 (pointA)
              8 LOAD_FAST                1 (pointB)
             10 BINARY_SUBTRACT
             12 CALL_FUNCTION            1
             14 STORE_FAST               2 (dist)

  3          16 LOAD_FAST                2 (dist)
             18 RETURN_VALUE

tout D'abord - chaque fois que nous l'appelons, nous devons faire une recherche globale pour "np", une recherche scoped pour "linalg" et une recherche scoped pour "norm", et le plafond de simplement appelant la fonction peut égaler des douzaines de python instruction.

enfin, nous avons perdu deux opérations pour stocker le résultat et le recharger pour le retourner...

premier passage à l'amélioration: rendre la recherche plus rapide, sauter le magasin

def distance(pointA, pointB, _norm=np.linalg.norm):
    return _norm(pointA - pointB)

Nous obtenons le beaucoup plus simplifié:

>>> dis.dis(distance)
  2           0 LOAD_FAST                2 (_norm)
              2 LOAD_FAST                0 (pointA)
              4 LOAD_FAST                1 (pointB)
              6 BINARY_SUBTRACT
              8 CALL_FUNCTION            1
             10 RETURN_VALUE

la fonction Appel overhead représente encore un certain travail, cependant. Et vous voudrez faire des points de repère pour déterminer si vous feriez mieux de faire le calcul. vous-même:

def distance(pointX, pointY):
    return (
        ((pointX.x - pointY.x) ** 2) +
        ((pointY.y - pointY.y) ** 2) +
        ((pointZ.z - pointZ.z) ** 2)
    ) ** 0.5  # fast sqrt

sur certaines plateformes, **0.5 est plus rapide que math.sqrt . Votre kilométrage peut varier.

**** remarques sur la performance.

pourquoi calculez-vous la distance? Si le seul but est de l'afficher,

 print("The target is %.2fm away" % (distance(a, b)))

avancez. Mais si vous comparez les distances, faites des vérifications de distance, etc. J'aimerais ajouter quelques performances utiles observations.

prenons deux cas: le tri par distance ou l'élimination d'une liste à des éléments qui répondent à une contrainte de gamme.

# Ultra naive implementations. Hold onto your hat.

def sort_things_by_distance(origin, things):
    return things.sort(key=lambda thing: distance(origin, thing))

def in_range(origin, range, things):
    things_in_range = []
    for thing in things:
        if distance(origin, thing) <= range:
            things_in_range.append(thing)

la première chose que nous devons nous rappeler est que nous utilisons Pythagore pour calculer la distance ( dist = sqrt(x^2 + y^2 + z^2) ) donc nous faisons beaucoup de sqrt appels. Math 101:

dist = root ( x^2 + y^2 + z^2 )
:.
dist^2 = x^2 + y^2 + z^2
and
sq(N) < sq(M) iff M > N
and
sq(N) > sq(M) iff N > M
and
sq(N) = sq(M) iff N == M

en bref: jusqu'à ce que nous exigions réellement la distance dans une unité de X plutôt que x^2, nous pouvons éliminer la la partie la plus dure des calculs.

# Still naive, but much faster.

def distance_sq(left, right):
    """ Returns the square of the distance between left and right. """
    return (
        ((left.x - right.x) ** 2) +
        ((left.y - right.y) ** 2) +
        ((left.z - right.z) ** 2)
    )

def sort_things_by_distance(origin, things):
    return things.sort(key=lambda thing: distance_sq(origin, thing))

def in_range(origin, range, things):
    things_in_range = []

    # Remember that sqrt(N)**2 == N, so if we square
    # range, we don't need to root the distances.
    range_sq = range**2

    for thing in things:
        if distance_sq(origin, thing) <= range_sq:
            things_in_range.append(thing)

Grand, les deux fonctions ne font plus de squareroots coûteux. Ce sera beaucoup plus rapide. Nous pouvons aussi améliorer in_range en le convertissant en générateur:

def in_range(origin, range, things):
    range_sq = range**2
    yield from (thing for thing in things
                if distance_sq(origin, thing) <= range_sq)

cela a particulièrement des avantages si vous faites quelque chose comme:

if any(in_range(origin, max_dist, things)):
    ...

Mais si la prochaine chose que vous allez faire nécessite une distance,

for nearby in in_range(origin, walking_distance, hotdog_stands):
    print("%s %.2fm" % (nearby.name, distance(origin, nearby)))

envisager de céder tuples:

def in_range_with_dist_sq(origin, range, things):
    range_sq = range**2
    for thing in things:
        dist_sq = distance_sq(origin, thing)
        if dist_sq <= range_sq: yield (thing, dist_sq)

cela peut être particulièrement utile si vous pouvez enchaîner les vérifications de portée ('trouver des choses qui sont près de X et à L'intérieur de Nm De Y', puisque vous n'avez pas à calculer la distance à nouveau).

mais qu'en est-il si nous cherchons une très grande liste de things et que nous prévoyons que beaucoup d'entre eux ne valent pas la peine d'être pris en considération?

il y a en fait une optimisation très simple:

def in_range_all_the_things(origin, range, things):
    range_sq = range**2
    for thing in things:
        dist_sq = (origin.x - thing.x) ** 2
        if dist_sq <= range_sq:
            dist_sq += (origin.y - thing.y) ** 2
            if dist_sq <= range_sq:
                dist_sq += (origin.z - thing.z) ** 2
                if dist_sq <= range_sq:
                    yield thing

si cela est utile dépendra de la taille des "choses".

def in_range_all_the_things(origin, range, things):
    range_sq = range**2
    if len(things) >= 4096:
        for thing in things:
            dist_sq = (origin.x - thing.x) ** 2
            if dist_sq <= range_sq:
                dist_sq += (origin.y - thing.y) ** 2
                if dist_sq <= range_sq:
                    dist_sq += (origin.z - thing.z) ** 2
                    if dist_sq <= range_sq:
                        yield thing
    elif len(things) > 32:
        for things in things:
            dist_sq = (origin.x - thing.x) ** 2
            if dist_sq <= range_sq:
                dist_sq += (origin.y - thing.y) ** 2 + (origin.z - thing.z) ** 2
                if dist_sq <= range_sq:
                    yield thing
    else:
        ... just calculate distance and range-check it ...

et de nouveau, envisager de céder le dist_sq. Notre exemple de hotdog devient alors:

# Chaining generators
info = in_range_with_dist_sq(origin, walking_distance, hotdog_stands)
info = (stand, dist_sq**0.5 for stand, dist_sq in info)
for stand, dist in info:
    print("%s %.2fm" % (stand, dist))

je trouve une fonction 'dist' dans matplotlib.mlab, mais je ne pense pas que ce soit assez pratique.

Je l'affiche ici juste pour référence.

import numpy as np
import matplotlib as plt

a = np.array([1, 2, 3])
b = np.array([2, 3, 4])

# Distance between a and b
dis = plt.mlab.dist(a, b)

Il peut être fait comme suit. Je ne sais pas à quelle vitesse c'est, mais ce n'est pas en utilisant num Py.

from math import sqrt
a = (1, 2, 3) # Data point 1
b = (4, 5, 6) # Data point 2
print sqrt(sum( (a - b)**2 for a, b in zip(a, b)))

ayant a et b comme vous les avez définis, vous pouvez utiliser aussi:

distance = np.sqrt(np.sum((a-b)**2))

Un joli one-liner:

dist = numpy.linalg.norm(a-b)

cependant, si la vitesse est un problème, je recommande d'expérimenter sur votre machine. J'ai trouvé que l'utilisation de la bibliothèque math sqrt avec l'opérateur ** pour le carré est beaucoup plus rapide sur ma machine que la solution mono-doublure.

j'ai fait mes tests en utilisant ce programme simple:

#!/usr/bin/python
import math
import numpy
from random import uniform

def fastest_calc_dist(p1,p2):
    return math.sqrt((p2[0] - p1[0]) ** 2 +
                     (p2[1] - p1[1]) ** 2 +
                     (p2[2] - p1[2]) ** 2)

def math_calc_dist(p1,p2):
    return math.sqrt(math.pow((p2[0] - p1[0]), 2) +
                     math.pow((p2[1] - p1[1]), 2) +
                     math.pow((p2[2] - p1[2]), 2))

def numpy_calc_dist(p1,p2):
    return numpy.linalg.norm(numpy.array(p1)-numpy.array(p2))

TOTAL_LOCATIONS = 1000

p1 = dict()
p2 = dict()
for i in range(0, TOTAL_LOCATIONS):
    p1[i] = (uniform(0,1000),uniform(0,1000),uniform(0,1000))
    p2[i] = (uniform(0,1000),uniform(0,1000),uniform(0,1000))

total_dist = 0
for i in range(0, TOTAL_LOCATIONS):
    for j in range(0, TOTAL_LOCATIONS):
        dist = fastest_calc_dist(p1[i], p2[j]) #change this line for testing
        total_dist += dist

print total_dist

sur ma machine, math_calc_dist court beaucoup plus vite que numpy_calc_dist : 1.5 secondes versus de 23,5 secondes .

Pour obtenir une différence mesurable entre fastest_calc_dist et math_calc_dist j'ai dû TOTAL_LOCATIONS à 6000. Puis fastest_calc_dist prend ~50 secondes tandis que math_calc_dist prend ~60 secondes .

vous pouvez également expérimenter avec numpy.sqrt et numpy.square bien que les deux aient été plus lents que le math alternatives sur ma machine.

mes tests ont été exécutés avec Python 2.6.6.

vous pouvez simplement soustraire les vecteurs et ensuite innerproduit.

suivant votre exemple,

a = numpy.array((xa, ya, za))
b = numpy.array((xb, yb, zb))

tmp = a - b
sum_squared = numpy.dot(tmp.T, tmp)
result sqrt(sum_squared)

C'est un code simple et facile à comprendre.

j'aime np.point (produit scalaire):

a = numpy.array((xa,ya,za))
b = numpy.array((xb,yb,zb))

distance = (np.dot(a-b,a-b))**.5

voici du code concis pour la distance euclidienne en Python avec deux points représentés en listes en Python.

def distance(v1,v2): 
    return sum([(x-y)**2 for (x,y) in zip(v1,v2)])**(0.5)

import numpy as np
from scipy.spatial import distance
input_arr = np.array([[0,3,0],[2,0,0],[0,1,3],[0,1,2],[-1,0,1],[1,1,1]]) 
test_case = np.array([0,0,0])
dst=[]
for i in range(0,6):
    temp = distance.euclidean(test_case,input_arr[i])
    dst.append(temp)
print(dst)

vous pouvez facilement utiliser la formule

distance = np.sqrt(np.sum(np.square(a-b)))

qui ne fait en fait rien de plus qu'utiliser le théorème de Pythagore pour calculer la distance, en ajoutant les carrés de Δx, Δy et Δz et en enracinant le résultat.

import math

dist = math.hypot(math.hypot(xa-xb, ya-yb), za-zb)

si vous voulez trouver la distance d'un point précis de la première des contractions que vous pouvez utiliser, plus vous pouvez le faire avec autant de dimensions que vous voulez.

import numpy as np

A = [3,4]
Dis = np.sqrt(A[0]**2 + A[1]**2)

Calculez la distance euclidienne pour l'espace multidimensionnel:

 import math

 x = [1, 2, 6] 
 y = [-2, 3, 2]

 dist = math.sqrt(sum([(xi-yi)**2 for xi,yi in zip(x, y)]))
 5.0990195135927845

trouver la différence de deux matrices en premier. Ensuite, appliquez la multiplication par élément avec la commande multiplier de num PY. Ensuite, trouver la sommation de l'élément sage multiplié nouvelle matrice. Enfin, trouver la racine carrée de la somme.

def findEuclideanDistance(a, b):
    euclidean_distance = a - b
    euclidean_distance = np.sum(np.multiply(euclidean_distance, euclidean_distance))
    euclidean_distance = np.sqrt(euclidean_distance)
    return euclidean_distance