Comment tracer un plan 3D dans Matlab?

voici un moyen facile de tracer l'avion en utilisant fill3:

points=[pointA' pointB' pointC']; % using the data given in the question
fill3(points(1,:),points(2,:),points(3,:),'r')
grid on
alpha(0.3)

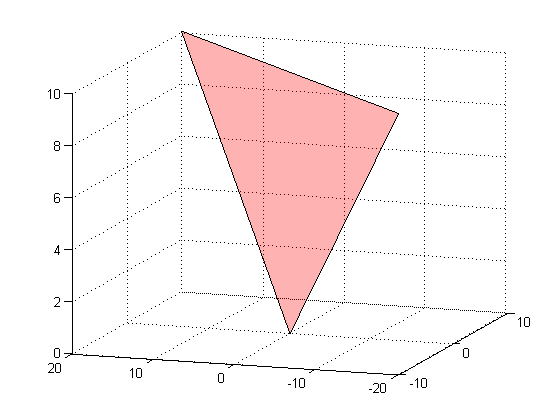
Vous avez déjà calculé le vecteur normal. Maintenant, vous devez décider quelles sont les limites de votre avion à l' x et z et créer un patch rectangulaire.

explication: chaque plan peut être caractérisé par son vecteur normal (A,B,C) et un autre coefficient D. L'équation du plan est AX+BY+CZ+D=0. Produit croisé entre deux différences entre les points,cross(P3-P1,P2-P1) permet de trouver (A,B,C). Afin de trouver D, mettez simplement n'importe quel point dans l'équation mentionnée ci-dessus:

   D = -Ax-By-Cz;

une fois que vous avez l'équation du plan, vous pouvez prendre 4 points qui se trouvent sur ce plan, et dessiner le patch entre eux.

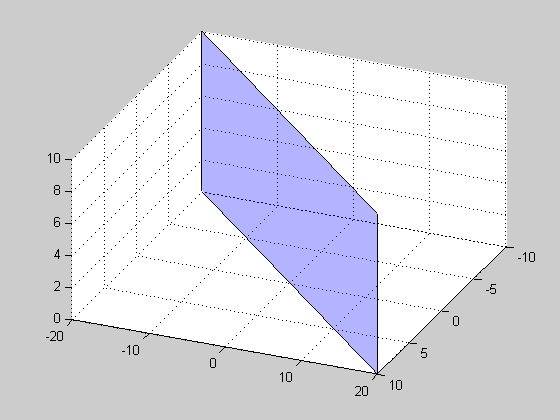
normal = cross(pointA-pointB, pointA-pointC); %# Calculate plane normal
%# Transform points to x,y,z
x = [pointA(1) pointB(1) pointC(1)];  
y = [pointA(2) pointB(2) pointC(2)];
z = [pointA(3) pointB(3) pointC(3)];

%Find all coefficients of plane equation    
A = normal(1); B = normal(2); C = normal(3);
D = -dot(normal,pointA);
%Decide on a suitable showing range
xLim = [min(x) max(x)];
zLim = [min(z) max(z)];
[X,Z] = meshgrid(xLim,zLim);
Y = (A * X + C * Z + D)/ (-B);
reOrder = [1 2  4 3];
figure();patch(X(reOrder),Y(reOrder),Z(reOrder),'b');
grid on;
alpha(0.3);

Voici ce que j'ai trouvé:

function [x, y, z] = plane_surf(normal, dist, size)

normal = normal / norm(normal);
center = normal * dist;

tangents = null(normal') * size;

res(1,1,:) = center + tangents * [-1;-1]; 
res(1,2,:) = center + tangents * [-1;1]; 
res(2,2,:) = center + tangents * [1;1]; 
res(2,1,:) = center + tangents * [1;-1];

x = squeeze(res(:,:,1));
y = squeeze(res(:,:,2));
z = squeeze(res(:,:,3));

end

que vous utiliseriez comme:

normal = cross(pointA-pointB, pointA-pointC);
dist = dot(normal, pointA)

[x, y, z] = plane_surf(normal, dist, 30);
surf(x, y, z);

qui trace un carré de côté de longueur 60 sur le plan en question

je veux ajouter à la réponse donnée par Andrey Rubshtein, son code fonctionne parfaitement sauf à B=0. Voici la version éditée de son code

le Code ci-dessous fonctionne quand A n'est pas 0

normal = cross(pointA-pointB, pointA-pointC); 
x = [pointA(1) pointB(1) pointC(1)];  
y = [pointA(2) pointB(2) pointC(2)];
z = [pointA(3) pointB(3) pointC(3)];  
A = normal(1); B = normal(2); C = normal(3);
D = -dot(normal,pointA);
zLim = [min(z) max(z)];
yLim = [min(y) max(y)];
[Y,Z] = meshgrid(yLim,zLim);
X = (C * Z + B * Y + D)/ (-A);
reOrder = [1 2  4 3];
figure();patch(X(reOrder),Y(reOrder),Z(reOrder),'r');
grid on;
alpha(0.3);

le Code ci-dessous fonctionne quand C n'est pas 0

normal = cross(pointA-pointB, pointA-pointC); 
x = [pointA(1) pointB(1) pointC(1)];  
y = [pointA(2) pointB(2) pointC(2)];
z = [pointA(3) pointB(3) pointC(3)];  
A = normal(1); B = normal(2); C = normal(3);
D = -dot(normal,pointA);
xLim = [min(x) max(x)];
yLim = [min(y) max(y)];
[Y,X] = meshgrid(yLim,xLim);
Z = (A * X + B * Y + D)/ (-C);
reOrder = [1 2  4 3];
figure();patch(X(reOrder),Y(reOrder),Z(reOrder),'r');
grid on;
alpha(0.3);