Comment puis-je déterminer si un Point 2D se trouve dans un polygone?
j'essaie de créer un fast point 2D à l'intérieur de l'algorithme polygon, pour l'utilisation dans les hit-testing (par exemple Polygon.contains(p:Point) ). Des Suggestions de techniques efficaces seraient les bienvenues.
30 réponses
pour les graphismes, je préfère ne pas préférer les entiers. De nombreux systèmes utilisent des entiers pour la peinture UI (les pixels sont des ints après tout), mais macOS par exemple utilise float pour tout. macOS ne connaît que les points et un point peut se traduire par un pixel, mais en fonction de la résolution du moniteur, il peut se traduire par autre chose. Sur les écrans rétiniens, un demi - point (0,5/0,5) est pixel. Pourtant, je n'ai jamais remarqué que les macOS UIs sont significativement plus lents que les autres UIs. Après tous les APIs 3D (OpenGL ou Direct3D) aussi fonctionne avec des flotteurs et des bibliothèques graphiques modernes très souvent profiter de L'accélération GPU.
Maintenant vous avez dit que la vitesse est votre principale préoccupation, OK, allons pour la vitesse. Avant d'exécuter un algorithme sophistiqué, faites d'abord un test simple. Créer un axis aligné délimitant la boîte autour de votre polygone. C'est très facile, rapide et peut déjà sûr beaucoup de calculs. Comment cela fonctionne? Itérer sur tous les points du polygone et trouver le min / max valeurs de X et Y.
E. G. vous avez les points (9/1), (4/3), (2/7), (8/2), (3/6) . Cela signifie que Xmin est 2, Xmax est 9, Ymin est 1 et Ymax est 7. Un point à l'extérieur du rectangle avec les deux bords (2/1) et (9/7) ne peut pas être dans le polygone.
// p is your point, p.x is the x coord, p.y is the y coord
if (p.x < Xmin || p.x > Xmax || p.y < Ymin || p.y > Ymax) {
// Definitely not within the polygon!
}
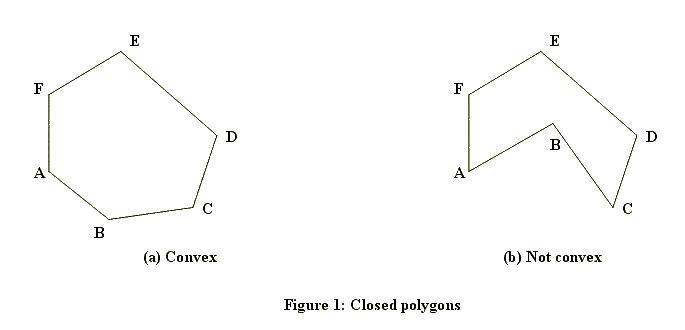
il s'agit du premier essai effectué pour un point quelconque. Comme vous pouvez le voir, ce test est ultra rapide, mais il est aussi très grossier. Pour gérer les points qui se trouvent dans le rectangle délimitant, nous avons besoin d'un algorithme plus sophistiqué. Il ya un couple de façons de comment cela peut être calculée. Quelle méthode fonctionne aussi dépend du fait si le polygone peut avoir des trous ou sera toujours solide. Voici des exemples de solides (un convexe, un concave):
et en voici un avec un trou:
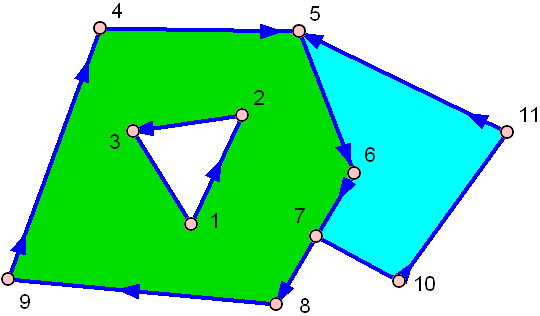
Le vert a un trou au milieu!
le plus facile algorithme, qui peut gérer les trois cas ci-dessus et est encore assez rapide est nommé ray casting . L'idée de l'algorithme est assez simple: dessinez un rayon virtuel de n'importe où à l'extérieur du polygone jusqu'à votre point et comptez combien de fois il frappe un côté du polygone. Si le nombre de coups est égal, c'est en dehors du polygone, si c'est impair, c'est à l'intérieur.
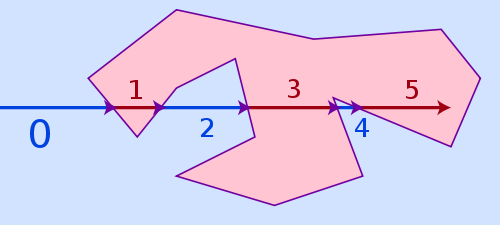
le numéro d'enroulement l'algorithme serait une alternative, il est plus précis pour les points étant très près d'une ligne polygonale, mais il est aussi beaucoup plus lent. La coulée de rayons peut échouer pour des points trop près d'un côté polygone en raison de la précision limitée de la pointe flottante et des problèmes d'arrondi, mais en réalité ce n'est pas un problème, comme si un point se trouve si près d'un côté, il est souvent visuellement pas même possible pour un spectateur de reconnaître si elle est déjà à l'intérieur ou encore à l'extérieur.
vous avez encore la boîte englobante de ci-dessus, vous vous souvenez? Il suffit de choisir un point à l'extérieur de la boîte englobante et l'utiliser comme point de départ de votre rayon. Par exemple: le point (Xmin - e/p.y) est à l'extérieur du polygone, c'est sûr.
mais qu'est-ce que e ? Eh bien, e (en fait epsilon) donne la boîte limite quelque rembourrage . Comme je l'ai dit, le traçage des rayons échoue si nous commençons trop près d'une ligne polygonale. Depuis la boîte englobante peut égaler le polygone (si le polygone est un axe aligné rectangle, la boîte limite est égale au polygone lui-même!), nous avons besoin de quelques rembourrage pour sûr, c'est tout. Quelle taille choisir e ? Pas trop grand. Cela dépend de l'échelle du système de coordonnées que vous utilisez pour le dessin. Si la largeur de pas de votre pixel est 1.0, alors choisissez 1.0 (et pourtant 0.1 aurait fonctionné aussi bien)
maintenant que nous avons le rayon avec ses coordonnées de début et de fin, le problème se déplace de " est le point dans le polygone " " combien de fois le rayon intersecte un polygone côté ". Par conséquent, nous ne pouvons pas simplement travailler avec les points polygones comme avant, maintenant nous avons besoin des côtés réels. Un côté est toujours défini par deux points.
side 1: (X1/Y1)-(X2/Y2)
side 2: (X2/Y2)-(X3/Y3)
side 3: (X3/Y3)-(X4/Y4)
:
vous devez tester le rayon contre tous les côtés. Considérez le rayon comme un vecteur et chaque côté comme un vecteur. Le rayon a frapper chaque côté exactement une fois ou jamais. Il ne peut pas frapper le même côté deux fois. Deux lignes dans l'espace 2D toujours se croisent exactement une fois, sauf s'ils sont parallèles, auquel cas ils ne se croisent jamais. Cependant, comme les vecteurs ont une longueur limitée, deux vecteurs peuvent ne pas être parallèles et ne jamais se croiser parce qu'ils sont trop courts pour se rencontrer.
// Test the ray against all sides
int intersections = 0;
for (side = 0; side < numberOfSides; side++) {
// Test if current side intersects with ray.
// If yes, intersections++;
}
if ((intersections & 1) == 1) {
// Inside of polygon
} else {
// Outside of polygon
}
jusqu'ici si bien, mais comment testez-vous si deux vecteurs se croisent? Voici un code C (non testé), qui devrait faire l'affaire:
#define NO 0
#define YES 1
#define COLLINEAR 2
int areIntersecting(
float v1x1, float v1y1, float v1x2, float v1y2,
float v2x1, float v2y1, float v2x2, float v2y2
) {
float d1, d2;
float a1, a2, b1, b2, c1, c2;
// Convert vector 1 to a line (line 1) of infinite length.
// We want the line in linear equation standard form: A*x + B*y + C = 0
// See: http://en.wikipedia.org/wiki/Linear_equation
a1 = v1y2 - v1y1;
b1 = v1x1 - v1x2;
c1 = (v1x2 * v1y1) - (v1x1 * v1y2);
// Every point (x,y), that solves the equation above, is on the line,
// every point that does not solve it, is not. The equation will have a
// positive result if it is on one side of the line and a negative one
// if is on the other side of it. We insert (x1,y1) and (x2,y2) of vector
// 2 into the equation above.
d1 = (a1 * v2x1) + (b1 * v2y1) + c1;
d2 = (a1 * v2x2) + (b1 * v2y2) + c1;
// If d1 and d2 both have the same sign, they are both on the same side
// of our line 1 and in that case no intersection is possible. Careful,
// 0 is a special case, that's why we don't test ">=" and "<=",
// but "<" and ">".
if (d1 > 0 && d2 > 0) return NO;
if (d1 < 0 && d2 < 0) return NO;
// The fact that vector 2 intersected the infinite line 1 above doesn't
// mean it also intersects the vector 1. Vector 1 is only a subset of that
// infinite line 1, so it may have intersected that line before the vector
// started or after it ended. To know for sure, we have to repeat the
// the same test the other way round. We start by calculating the
// infinite line 2 in linear equation standard form.
a2 = v2y2 - v2y1;
b2 = v2x1 - v2x2;
c2 = (v2x2 * v2y1) - (v2x1 * v2y2);
// Calculate d1 and d2 again, this time using points of vector 1.
d1 = (a2 * v1x1) + (b2 * v1y1) + c2;
d2 = (a2 * v1x2) + (b2 * v1y2) + c2;
// Again, if both have the same sign (and neither one is 0),
// no intersection is possible.
if (d1 > 0 && d2 > 0) return NO;
if (d1 < 0 && d2 < 0) return NO;
// If we get here, only two possibilities are left. Either the two
// vectors intersect in exactly one point or they are collinear, which
// means they intersect in any number of points from zero to infinite.
if ((a1 * b2) - (a2 * b1) == 0.0f) return COLLINEAR;
// If they are not collinear, they must intersect in exactly one point.
return YES;
}
Les valeurs d'entrée sont les deux paramètres du vecteur 1 ( v1x1/v1y1 et v1x2/v1y2 ) et du vecteur 2 ( v2x1/v2y1 et v2x2/v2y2 ). Donc vous avez 2 vecteurs, 4 points, 8 coordonnées. YES et NO sont clairs. YES augmente les intersections, NO ne fait rien.
et COLLINEAR? Cela signifie que les deux vecteurs se trouvent sur la même ligne infinie, selon la position et la longueur, ils ne se croisent pas du tout ou ils se croisent dans un nombre infini de point. Je ne sais pas comment gérer cette affaire, Je ne la considérerais pas comme une intersection. Eh bien , ce cas est assez rare dans la pratique de toute façon en raison d'erreurs d'arrondi à virgule flottante; un meilleur code ne serait probablement pas tester pour == 0.0f , mais plutôt pour quelque chose comme < epsilon , où epsilon est un nombre plutôt petit.
Si vous avez besoin de tester un plus grand nombre de points, vous pouvez certainement d'accélérer le tout un peu en gardant l'équation linéaire les formes standard des côtés polygonaux dans la mémoire, de sorte que vous n'avez pas à recalculer ceux-ci à chaque fois. Cela vous permettra d'économiser deux multiplications de points flottants et trois soustractions de points flottants sur chaque test en échange de stocker trois valeurs de points flottants par côté de polygone en mémoire. C'est un compromis mémoire vs temps de calcul typique.
Last but not least: si vous pouvez utiliser du matériel 3D pour résoudre le problème, il existe une alternative intéressante. Laissez le GPU faire tout ce qu'il faut. le travail pour vous. Créer une surface de peinture qui est hors de l'écran. Remplir complètement avec la couleur noire. Maintenant, laissez OpenGL ou Direct3D peindre votre polygone(ou même tous vos polygones si vous voulez juste tester si le point est dans l'un d'eux, mais vous ne vous souciez pas de lequel) et remplissez le (s) polygone (s) avec une couleur différente, par exemple blanc. Pour vérifier si un point est à l'intérieur du polygone, obtenez la couleur de ce point à partir de la surface de dessin. C'est juste un O(1) mémoire de fetch.
de bien sûr cette méthode n'est utilisable que si votre surface de dessin ne doit pas être énorme. Si elle ne peut pas rentrer dans la mémoire GPU, cette méthode est plus lente que de le faire sur le CPU. Si cela doit être énorme et que votre GPU supporte les shaders modernes, vous pouvez toujours utiliser le GPU en implémentant le ray casting montré ci-dessus comme un GPU shader, ce qui est absolument possible. Pour un plus grand nombre de polygones ou un grand nombre de points à tester, cela va payer, envisager certains GPU sera en mesure de tester 64 à 256 points parallèlement. Notez cependant que le transfert de données du CPU au GPU et vice-versa est toujours coûteux, donc pour tester quelques points par rapport à quelques polygones simples, où soit les points soit les polygones sont dynamiques et changeront fréquemment, une approche GPU sera rarement payante.
je pense que le morceau de code suivant est la meilleure solution (prise de ici ):
int pnpoly(int nvert, float *vertx, float *verty, float testx, float testy)
{
int i, j, c = 0;
for (i = 0, j = nvert-1; i < nvert; j = i++) {
if ( ((verty[i]>testy) != (verty[j]>testy)) &&
(testx < (vertx[j]-vertx[i]) * (testy-verty[i]) / (verty[j]-verty[i]) + vertx[i]) )
c = !c;
}
return c;
}
Arguments
- nvert : nombre de sommets dans le polygone. La question de savoir s'il convient de répéter le premier vertex à la fin a été examinée dans l'article précité.
- vertx, verty : tableaux contenant les coordonnées x - et y de la polygone de sommets.
- testx, testy : coordonnées X et y du point d'essai.
il est à la fois court et efficace et fonctionne à la fois pour les polygones convexes et concaves. Comme indiqué précédemment, vous devriez d'abord vérifier le rectangle limite et traiter les trous de polygone séparément.
l'idée derrière ceci est assez simple. L'auteur le décrit comme suit:
I exécuter un rayon semi-infini horizontalement (augmentant x, Fixe y) à partir du point d'essai, et compter combien d'arêtes il croise. À chaque passage, le rayon commute entre l'intérieur et l'extérieur. C'est ce qu'on appelle le théorème de la courbe de Jordan.
la variable c passe de 0 à 1 et de 1 à 0 chaque fois que le rayon horizontal croise un bord. Donc en gros, il s'agit de savoir si le nombre de bords croisés est pair ou impair. 0 signifie Pair et 1 signifie Impair.
Voici une version C# de la réponse donnée par nirg , qui vient de ce professeur de RPI . Il est à noter que l'utilisation du code de cette source RPI nécessite une attribution.
une case à cocher a été ajoutée en haut. Toutefois, comme le souligne James Brown, le code principal est presque aussi rapide que la case de limitation elle-même, de sorte que la case de Limitation peut en fait ralentir l'ensemble de l'opération, dans le cas où la plupart des points de vérification sont à l'intérieur de la boîte englobante. Ainsi, vous pouvez laisser la boîte englobante découvrez, ou une autre solution serait de précalculer les cases de votre polygones s'ils ne changent pas de forme trop souvent.
public bool IsPointInPolygon( Point p, Point[] polygon )
{
double minX = polygon[ 0 ].X;
double maxX = polygon[ 0 ].X;
double minY = polygon[ 0 ].Y;
double maxY = polygon[ 0 ].Y;
for ( int i = 1 ; i < polygon.Length ; i++ )
{
Point q = polygon[ i ];
minX = Math.Min( q.X, minX );
maxX = Math.Max( q.X, maxX );
minY = Math.Min( q.Y, minY );
maxY = Math.Max( q.Y, maxY );
}
if ( p.X < minX || p.X > maxX || p.Y < minY || p.Y > maxY )
{
return false;
}
// http://www.ecse.rpi.edu/Homepages/wrf/Research/Short_Notes/pnpoly.html
bool inside = false;
for ( int i = 0, j = polygon.Length - 1 ; i < polygon.Length ; j = i++ )
{
if ( ( polygon[ i ].Y > p.Y ) != ( polygon[ j ].Y > p.Y ) &&
p.X < ( polygon[ j ].X - polygon[ i ].X ) * ( p.Y - polygon[ i ].Y ) / ( polygon[ j ].Y - polygon[ i ].Y ) + polygon[ i ].X )
{
inside = !inside;
}
}
return inside;
}
voici une variante JavaScript de la réponse de M. Katz basée sur l'approche de Nirg:
function pointIsInPoly(p, polygon) {
var isInside = false;
var minX = polygon[0].x, maxX = polygon[0].x;
var minY = polygon[0].y, maxY = polygon[0].y;
for (var n = 1; n < polygon.length; n++) {
var q = polygon[n];
minX = Math.min(q.x, minX);
maxX = Math.max(q.x, maxX);
minY = Math.min(q.y, minY);
maxY = Math.max(q.y, maxY);
}
if (p.x < minX || p.x > maxX || p.y < minY || p.y > maxY) {
return false;
}
var i = 0, j = polygon.length - 1;
for (i, j; i < polygon.length; j = i++) {
if ( (polygon[i].y > p.y) != (polygon[j].y > p.y) &&
p.x < (polygon[j].x - polygon[i].x) * (p.y - polygon[i].y) / (polygon[j].y - polygon[i].y) + polygon[i].x ) {
isInside = !isInside;
}
}
return isInside;
}
calcule la somme orientée des angles entre le point p et chacun des sommets du polygone. Si l'angle orienté total est de 360 degrés, le point est à l'intérieur. Si le total est 0, le point est à l'extérieur.
je préfère cette méthode parce qu'elle est plus robuste et moins dépendante de la précision numérique.
méthodes qui calculent l'équitabilité du nombre d'intersections sont limités parce que vous pouvez 'hit' un apex pendant le calcul du nombre de intersection.
EDIT: Par ailleurs, cette méthode fonctionne avec concaves et convexes des polygones.
EDIT: j'ai récemment trouvé un tout article Wikipedia sur le sujet.
Le Eric Haines article cité par bobobobo est vraiment excellent. Particulièrement intéressant sont les tableaux comparant la performance des algorithmes; la méthode de sommation angle est vraiment mauvais par rapport aux autres. Il est également intéressant de noter que des optimisations comme l'utilisation d'une grille de recherche pour subdiviser davantage le polygone en secteurs "in" et "out" peuvent rendre le test incroyablement rapide même sur des polygones avec > 1000 côtés.
de toute façon, il est tôt mais mon vote va à la méthode "crossings", qui est à peu près ce que Mecki décrit je pense. Cependant je l'ai trouvé le plus succinctement décrit et codifié par David Bourke . J'aime qu'il n'y a pas de véritable trigonométrie nécessaire, et il travaille pour convexes et concaves, et il fonctionne raisonnablement bien que le nombre de côtés augmente.
soit dit en passant, voici une des tables de performances de L'article d'Eric Haines pour interest, testant sur des polygones aléatoires.
number of edges per polygon
3 4 10 100 1000
MacMartin 2.9 3.2 5.9 50.6 485
Crossings 3.1 3.4 6.8 60.0 624
Triangle Fan+edge sort 1.1 1.8 6.5 77.6 787
Triangle Fan 1.2 2.1 7.3 85.4 865
Barycentric 2.1 3.8 13.8 160.7 1665
Angle Summation 56.2 70.4 153.6 1403.8 14693
Grid (100x100) 1.5 1.5 1.6 2.1 9.8
Grid (20x20) 1.7 1.7 1.9 5.7 42.2
Bins (100) 1.8 1.9 2.7 15.1 117
Bins (20) 2.1 2.2 3.7 26.3 278
cette question est si intéressante. J'ai une autre idée réalisable différent des autres réponses de ce post.
L'idée est d'utiliser la somme des angles de décider si la cible est à l'intérieur ou à l'extérieur. Si la cible est à l'intérieur d'une zone, la somme de l'angle forme par la cible et tous les deux points de la frontière sera 360. Si la cible est à l'extérieur, la somme ne sera pas 360. L'angle a une direction. Si l'angle d'aller vers l'arrière, l'angle est négatif. C'est juste comme calcul du numéro d'enroulement .
se référer à cette image pour obtenir une compréhension de base de l'idée:
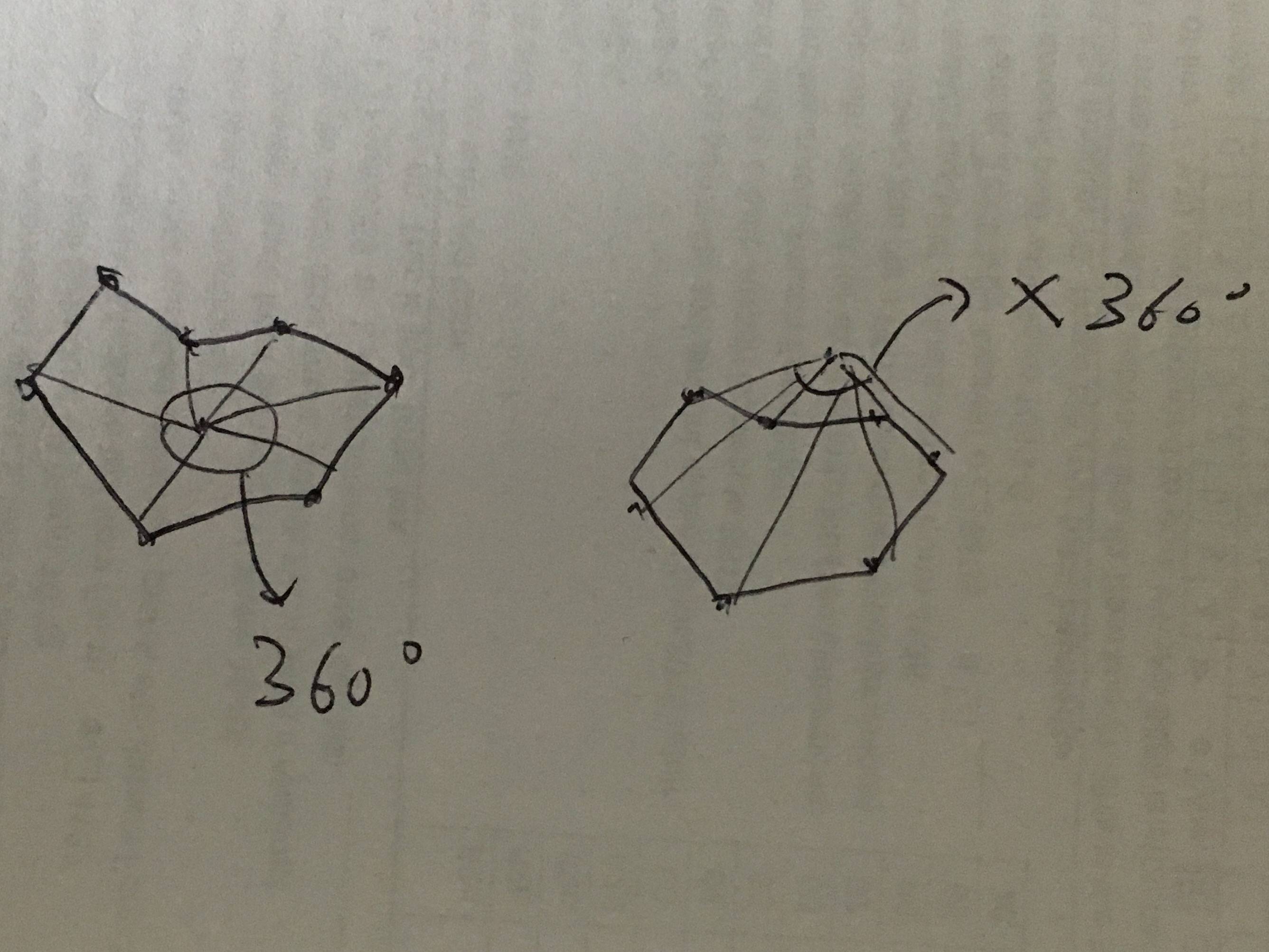
mon algorithme suppose que le sens des aiguilles d'une montre est la direction positive. Voici une entrée potentielle:
[[-122.402015, 48.225216], [-117.032049, 48.999931], [-116.919132, 45.995175], [-124.079107, 46.267259], [-124.717175, 48.377557], [-122.92315, 47.047963], [-122.402015, 48.225216]]
voici le code python qui implémente l'idée:
def isInside(self, border, target):
degree = 0
for i in range(len(border) - 1):
a = border[i]
b = border[i + 1]
# calculate distance of vector
A = getDistance(a[0], a[1], b[0], b[1]);
B = getDistance(target[0], target[1], a[0], a[1])
C = getDistance(target[0], target[1], b[0], b[1])
# calculate direction of vector
ta_x = a[0] - target[0]
ta_y = a[1] - target[1]
tb_x = b[0] - target[0]
tb_y = b[1] - target[1]
cross = tb_y * ta_x - tb_x * ta_y
clockwise = cross < 0
# calculate sum of angles
if(clockwise):
degree = degree + math.degrees(math.acos((B * B + C * C - A * A) / (2.0 * B * C)))
else:
degree = degree - math.degrees(math.acos((B * B + C * C - A * A) / (2.0 * B * C)))
if(abs(round(degree) - 360) <= 3):
return True
return False
j'ai fait quelques travaux sur ce Dos quand j'étais un chercheur sous Michael Stonebraker - vous savez, le professeur qui est venu avec Ingres , PostgreSQL , etc.
nous avons réalisé que le moyen le plus rapide était d'abord de faire une boîte limite parce que C'est SUPER rapide. Si c'est en dehors de la boîte englobante, c'est à l'extérieur. Sinon, vous ne les plus difficiles à travailler...
si vous voulez un grand algorithme, regardez le code source PostgreSQL du projet open source pour le travail geo...
je tiens à souligner, nous n'avons jamais eu aucun aperçu dans la droite vs gauche handedness (aussi expressible comme un" intérieur "vs" extérieur " problème...
mise à JOUR
le lien de BKB fournit un bon nombre d'algorithmes raisonnables. Je travaillais sur les problèmes des sciences de la Terre et donc besoin d'une solution qui fonctionne en latitude/longitude, et il a le problème particulier de chiralité - est de la zone à l'intérieur de la zone plus petite ou la plus grande région? La réponse est que la "direction" de la verticies questions - c'est soit gaucher ou droitier, et de cette façon vous pouvez indiquer soit "à l'intérieur" d'un polygone donné. Ainsi, mon travail a utilisé la solution trois énumérée sur cette page.
en outre, mon travail a utilisé des fonctions séparées pour les tests" en ligne".
...Depuis que quelqu'un a demandé: nous avons pensé de ce que les tests de la boîte de limite étaient meilleurs quand le nombre de vertiges est allé au - delà d'un certain nombre-Faire un test très rapide avant de faire le test plus long si nécessaire... Une boîte limite est créée en prenant simplement le plus grand x, le plus petit x, le plus grand y et le plus petit y et en les mettant ensemble pour faire quatre points de la boîte...
un autre conseil pour ceux qui suivent: nous avons fait tous nos plus sophistiqué et "light-dimming" calcul dans un espace de grille tout en points positifs sur un plan et puis réinjecté dans la longitude/latitude" réelle", évitant ainsi les erreurs éventuelles de contournement lorsqu'on croise la ligne 180 de longitude et lorsqu'on manipule des régions polaires. A très bien fonctionné!
aime vraiment la solution Postée par Nirg et éditée par bobobobo. Je viens de le rendre javascript convivial et un peu plus lisible pour mon usage:
function insidePoly(poly, pointx, pointy) {
var i, j;
var inside = false;
for (i = 0, j = poly.length - 1; i < poly.length; j = i++) {
if(((poly[i].y > pointy) != (poly[j].y > pointy)) && (pointx < (poly[j].x-poly[i].x) * (pointy-poly[i].y) / (poly[j].y-poly[i].y) + poly[i].x) ) inside = !inside;
}
return inside;
}
version Swift de la réponse de nirg :
extension CGPoint {
func isInsidePolygon(vertices: [CGPoint]) -> Bool {
guard !vertices.isEmpty else { return false }
var j = vertices.last!, c = false
for i in vertices {
let a = (i.y > y) != (j.y > y)
let b = (x < (j.x - i.x) * (y - i.y) / (j.y - i.y) + i.x)
if a && b { c = !c }
j = i
}
return c
}
}
la réponse de David Segond est à peu près la réponse générale standard, et Richard T est l'optimisation la plus commune, bien que therre sont quelques autres. D'autres optimisations fortes sont basées sur des solutions moins générales. Par exemple, si vous allez vérifier le même polygone avec beaucoup de points, la triangulation du polygone peut accélérer considérablement les choses comme il ya un certain nombre d'algorithmes de recherche de fer-blanc très rapide. Une autre est si le polygone et les points sont sur un plan limité à basse résolution, par exemple un écran, vous pouvez peindre le polygone sur un tampon d'affichage mappé en mémoire dans une couleur donnée, et vérifier la couleur d'un pixel donné pour voir s'il se trouve dans les polygones.
comme de nombreuses optimisations, celles-ci sont basées sur des cas spécifiques plutôt que sur des cas généraux, et produisent des bénéfices basés sur le temps amorti plutôt que sur un usage unique.
travaillant dans ce domaine, J'ai trouvé Joeseph O'Rourkes 'Computation Geometry in C' ISBN 0-521-44034-3 pour être une grande aide.
la solution triviale serait de diviser le polygone en triangles et de frapper tester les triangles comme expliqué ici
si votre polygone est convexe il pourrait y avoir une meilleure approche cependant. Regarder le polygone comme un ensemble infini de lignes. Chaque ligne divisant l'espace en deux. pour chaque point il est facile de dire si son sur les un côté ou de l'autre côté de la ligne. Si un point est du même côté de toutes les lignes alors il est à l'intérieur du polygone.
je sais que c'est ancien, mais voici un algorithme de moulage de rayons implémenté dans Cocoa, au cas où quelqu'un serait intéressé. Pas sûr que ce soit la façon la plus efficace de faire les choses, mais il peut aider quelqu'un.
- (BOOL)shape:(NSBezierPath *)path containsPoint:(NSPoint)point
{
NSBezierPath *currentPath = [path bezierPathByFlatteningPath];
BOOL result;
float aggregateX = 0; //I use these to calculate the centroid of the shape
float aggregateY = 0;
NSPoint firstPoint[1];
[currentPath elementAtIndex:0 associatedPoints:firstPoint];
float olderX = firstPoint[0].x;
float olderY = firstPoint[0].y;
NSPoint interPoint;
int noOfIntersections = 0;
for (int n = 0; n < [currentPath elementCount]; n++) {
NSPoint points[1];
[currentPath elementAtIndex:n associatedPoints:points];
aggregateX += points[0].x;
aggregateY += points[0].y;
}
for (int n = 0; n < [currentPath elementCount]; n++) {
NSPoint points[1];
[currentPath elementAtIndex:n associatedPoints:points];
//line equations in Ax + By = C form
float _A_FOO = (aggregateY/[currentPath elementCount]) - point.y;
float _B_FOO = point.x - (aggregateX/[currentPath elementCount]);
float _C_FOO = (_A_FOO * point.x) + (_B_FOO * point.y);
float _A_BAR = olderY - points[0].y;
float _B_BAR = points[0].x - olderX;
float _C_BAR = (_A_BAR * olderX) + (_B_BAR * olderY);
float det = (_A_FOO * _B_BAR) - (_A_BAR * _B_FOO);
if (det != 0) {
//intersection points with the edges
float xIntersectionPoint = ((_B_BAR * _C_FOO) - (_B_FOO * _C_BAR)) / det;
float yIntersectionPoint = ((_A_FOO * _C_BAR) - (_A_BAR * _C_FOO)) / det;
interPoint = NSMakePoint(xIntersectionPoint, yIntersectionPoint);
if (olderX <= points[0].x) {
//doesn't matter in which direction the ray goes, so I send it right-ward.
if ((interPoint.x >= olderX && interPoint.x <= points[0].x) && (interPoint.x > point.x)) {
noOfIntersections++;
}
} else {
if ((interPoint.x >= points[0].x && interPoint.x <= olderX) && (interPoint.x > point.x)) {
noOfIntersections++;
}
}
}
olderX = points[0].x;
olderY = points[0].y;
}
if (noOfIntersections % 2 == 0) {
result = FALSE;
} else {
result = TRUE;
}
return result;
}
Obj-C version de nirg de réponse avec la méthode de l'échantillon pour l'essai de points. La réponse de Nirg a bien fonctionné pour moi.
- (BOOL)isPointInPolygon:(NSArray *)vertices point:(CGPoint)test {
NSUInteger nvert = [vertices count];
NSInteger i, j, c = 0;
CGPoint verti, vertj;
for (i = 0, j = nvert-1; i < nvert; j = i++) {
verti = [(NSValue *)[vertices objectAtIndex:i] CGPointValue];
vertj = [(NSValue *)[vertices objectAtIndex:j] CGPointValue];
if (( (verti.y > test.y) != (vertj.y > test.y) ) &&
( test.x < ( vertj.x - verti.x ) * ( test.y - verti.y ) / ( vertj.y - verti.y ) + verti.x) )
c = !c;
}
return (c ? YES : NO);
}
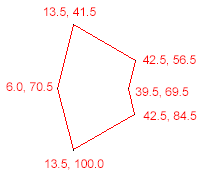
- (void)testPoint {
NSArray *polygonVertices = [NSArray arrayWithObjects:
[NSValue valueWithCGPoint:CGPointMake(13.5, 41.5)],
[NSValue valueWithCGPoint:CGPointMake(42.5, 56.5)],
[NSValue valueWithCGPoint:CGPointMake(39.5, 69.5)],
[NSValue valueWithCGPoint:CGPointMake(42.5, 84.5)],
[NSValue valueWithCGPoint:CGPointMake(13.5, 100.0)],
[NSValue valueWithCGPoint:CGPointMake(6.0, 70.5)],
nil
];
CGPoint tappedPoint = CGPointMake(23.0, 70.0);
if ([self isPointInPolygon:polygonVertices point:tappedPoint]) {
NSLog(@"YES");
} else {
NSLog(@"NO");
}
}
moi aussi je pensais que la sommation 360 ne fonctionnait que pour les polygones convexes mais ce n'est pas vrai.
ce site a un beau diagramme montrant exactement cela, et une bonne explication sur le test de succès: Gamasutra - de s'Écraser dans la Nouvelle Année: la Détection de Collision
version C# de la réponse de nirg est ici: je vais juste partager le code. Ça pourrait faire gagner du temps à quelqu'un.
public static bool IsPointInPolygon(IList<Point> polygon, Point testPoint) {
bool result = false;
int j = polygon.Count() - 1;
for (int i = 0; i < polygon.Count(); i++) {
if (polygon[i].Y < testPoint.Y && polygon[j].Y >= testPoint.Y || polygon[j].Y < testPoint.Y && polygon[i].Y >= testPoint.Y) {
if (polygon[i].X + (testPoint.Y - polygon[i].Y) / (polygon[j].Y - polygon[i].Y) * (polygon[j].X - polygon[i].X) < testPoint.X) {
result = !result;
}
}
j = i;
}
return result;
}
Version Java:
public class Geocode {
private float latitude;
private float longitude;
public Geocode() {
}
public Geocode(float latitude, float longitude) {
this.latitude = latitude;
this.longitude = longitude;
}
public float getLatitude() {
return latitude;
}
public void setLatitude(float latitude) {
this.latitude = latitude;
}
public float getLongitude() {
return longitude;
}
public void setLongitude(float longitude) {
this.longitude = longitude;
}
}
public class GeoPolygon {
private ArrayList<Geocode> points;
public GeoPolygon() {
this.points = new ArrayList<Geocode>();
}
public GeoPolygon(ArrayList<Geocode> points) {
this.points = points;
}
public GeoPolygon add(Geocode geo) {
points.add(geo);
return this;
}
public boolean inside(Geocode geo) {
int i, j;
boolean c = false;
for (i = 0, j = points.size() - 1; i < points.size(); j = i++) {
if (((points.get(i).getLongitude() > geo.getLongitude()) != (points.get(j).getLongitude() > geo.getLongitude())) &&
(geo.getLatitude() < (points.get(j).getLatitude() - points.get(i).getLatitude()) * (geo.getLongitude() - points.get(i).getLongitude()) / (points.get(j).getLongitude() - points.get(i).getLongitude()) + points.get(i).getLatitude()))
c = !c;
}
return c;
}
}
.Port Net:
static void Main(string[] args)
{
Console.Write("Hola");
List<double> vertx = new List<double>();
List<double> verty = new List<double>();
int i, j, c = 0;
vertx.Add(1);
vertx.Add(2);
vertx.Add(1);
vertx.Add(4);
vertx.Add(4);
vertx.Add(1);
verty.Add(1);
verty.Add(2);
verty.Add(4);
verty.Add(4);
verty.Add(1);
verty.Add(1);
int nvert = 6; //Vértices del poligono
double testx = 2;
double testy = 5;
for (i = 0, j = nvert - 1; i < nvert; j = i++)
{
if (((verty[i] > testy) != (verty[j] > testy)) &&
(testx < (vertx[j] - vertx[i]) * (testy - verty[i]) / (verty[j] - verty[i]) + vertx[i]))
c = 1;
}
}
il n'y a rien de plus beau qu'une définition inductive d'un problème. Pour être complet ici vous avez une version dans prolog qui pourrait aussi clarifier les thoughs derrière ray casting :
basé sur la simulation de l'algorithme de simplicité dans http://www.ecse.rpi.edu/Homepages/wrf/Research/Short_Notes/pnpoly.html
Certains helper prédicats:
exor(A,B):- \+A,B;A,\+B.
in_range(Coordinate,CA,CB) :- exor((CA>Coordinate),(CB>Coordinate)).
inside(false).
inside(_,[_|[]]).
inside(X:Y, [X1:Y1,X2:Y2|R]) :- in_range(Y,Y1,Y2), X > ( ((X2-X1)*(Y-Y1))/(Y2-Y1) + X1),toggle_ray, inside(X:Y, [X2:Y2|R]); inside(X:Y, [X2:Y2|R]).
get_line(_,_,[]).
get_line([XA:YA,XB:YB],[X1:Y1,X2:Y2|R]):- [XA:YA,XB:YB]=[X1:Y1,X2:Y2]; get_line([XA:YA,XB:YB],[X2:Y2|R]).
l'équation d'une ligne donnée 2 points A et B (Ligne(A,B)) est:
(YB-YA)
Y - YA = ------- * (X - XA)
(XB-YB)
il est important que le sens de rotation de la ligne soit sertie de montre, pour les limites et anti-horaire pour les trous. Nous allons vérifier si le point (X, Y), I. e le point d'essai est à gauche demi-plan de notre ligne (c'est une question de goût, il pourrait aussi être le côté droit, mais aussi la direction des lignes de limites doit être changé en ce cas), c'est à projeter le rayon du point à droite (ou à gauche)) et reconnaissez l'intersection avec la ligne. Nous avons choisi de projet le rayon dans la direction horizontale (encore une question de goût, cela pourrait aussi être fait en vertical avec des restrictions similaires), de sorte que nous avons:
(XB-XA)
X < ------- * (Y - YA) + XA
(YB-YA)
Maintenant, nous avons besoin de savoir si le point est à gauche (ou à droite) de le segment de ligne seulement, pas l'avion entier, donc nous devons restreindre la recherche à ce segment, mais c'est facile depuis à l'intérieur du segment de seulement un point dans la ligne peut être plus élevé que de Y dans l'axe vertical. Comme il s'agit d'une restriction plus forte doit être le premier à vérifier, donc nous prenons d'abord seulement ces lignes répondre à cette exigence et ensuite vérifier sa position. Par la Jordanie Théorème de courbe tout rayon projeté à un polygone doit se croiser à un même nombre de lignes. Donc nous avons fini, nous allons jeter le rayon à la à chaque fois qu'il croise une ligne, il bascule son état. Toutefois, dans notre mise en œuvre nous sont goint pour vérifier la longueur de le sac de solutions répondant aux restrictions données et de décider de la innership sur elle. pour chaque ligne dans le polygone cela doit être fait.
is_left_half_plane(_,[],[],_).
is_left_half_plane(X:Y,[XA:YA,XB:YB], [[X1:Y1,X2:Y2]|R], Test) :- [XA:YA, XB:YB] = [X1:Y1, X2:Y2], call(Test, X , (((XB - XA) * (Y - YA)) / (YB - YA) + XA));
is_left_half_plane(X:Y, [XA:YA, XB:YB], R, Test).
in_y_range_at_poly(Y,[XA:YA,XB:YB],Polygon) :- get_line([XA:YA,XB:YB],Polygon), in_range(Y,YA,YB).
all_in_range(Coordinate,Polygon,Lines) :- aggregate(bag(Line), in_y_range_at_poly(Coordinate,Line,Polygon), Lines).
traverses_ray(X:Y, Lines, Count) :- aggregate(bag(Line), is_left_half_plane(X:Y, Line, Lines, <), IntersectingLines), length(IntersectingLines, Count).
% This is the entry point predicate
inside_poly(X:Y,Polygon,Answer) :- all_in_range(Y,Polygon,Lines), traverses_ray(X:Y, Lines, Count), (1 is mod(Count,2)->Answer=inside;Answer=outside).
VBA VERSION:
Note: rappelez-vous que si votre polygone est une zone à l'intérieur d'une carte que la Latitude/Longitude sont des valeurs Y/X par opposition à X/Y (Latitude = Y, Longitude = X) en raison de ce que je comprends sont des implications historiques de retour quand la Longitude n'était pas une mesure.
MODULE de classe: CPoint
Private pXValue As Double
Private pYValue As Double
'''''X Value Property'''''
Public Property Get X() As Double
X = pXValue
End Property
Public Property Let X(Value As Double)
pXValue = Value
End Property
'''''Y Value Property'''''
Public Property Get Y() As Double
Y = pYValue
End Property
Public Property Let Y(Value As Double)
pYValue = Value
End Property
MODULE:
Public Function isPointInPolygon(p As CPoint, polygon() As CPoint) As Boolean
Dim i As Integer
Dim j As Integer
Dim q As Object
Dim minX As Double
Dim maxX As Double
Dim minY As Double
Dim maxY As Double
minX = polygon(0).X
maxX = polygon(0).X
minY = polygon(0).Y
maxY = polygon(0).Y
For i = 1 To UBound(polygon)
Set q = polygon(i)
minX = vbMin(q.X, minX)
maxX = vbMax(q.X, maxX)
minY = vbMin(q.Y, minY)
maxY = vbMax(q.Y, maxY)
Next i
If p.X < minX Or p.X > maxX Or p.Y < minY Or p.Y > maxY Then
isPointInPolygon = False
Exit Function
End If
' SOURCE: http://www.ecse.rpi.edu/Homepages/wrf/Research/Short_Notes/pnpoly.html
isPointInPolygon = False
i = 0
j = UBound(polygon)
Do While i < UBound(polygon) + 1
If (polygon(i).Y > p.Y) Then
If (polygon(j).Y < p.Y) Then
If p.X < (polygon(j).X - polygon(i).X) * (p.Y - polygon(i).Y) / (polygon(j).Y - polygon(i).Y) + polygon(i).X Then
isPointInPolygon = True
Exit Function
End If
End If
ElseIf (polygon(i).Y < p.Y) Then
If (polygon(j).Y > p.Y) Then
If p.X < (polygon(j).X - polygon(i).X) * (p.Y - polygon(i).Y) / (polygon(j).Y - polygon(i).Y) + polygon(i).X Then
isPointInPolygon = True
Exit Function
End If
End If
End If
j = i
i = i + 1
Loop
End Function
Function vbMax(n1, n2) As Double
vbMax = IIf(n1 > n2, n1, n2)
End Function
Function vbMin(n1, n2) As Double
vbMin = IIf(n1 > n2, n2, n1)
End Function
Sub TestPointInPolygon()
Dim i As Integer
Dim InPolygon As Boolean
' MARKER Object
Dim p As CPoint
Set p = New CPoint
p.X = <ENTER X VALUE HERE>
p.Y = <ENTER Y VALUE HERE>
' POLYGON OBJECT
Dim polygon() As CPoint
ReDim polygon(<ENTER VALUE HERE>) 'Amount of vertices in polygon - 1
For i = 0 To <ENTER VALUE HERE> 'Same value as above
Set polygon(i) = New CPoint
polygon(i).X = <ASSIGN X VALUE HERE> 'Source a list of values that can be looped through
polgyon(i).Y = <ASSIGN Y VALUE HERE> 'Source a list of values that can be looped through
Next i
InPolygon = isPointInPolygon(p, polygon)
MsgBox InPolygon
End Sub
indique un point dans le test de polygone en C qui n'utilise pas de Ray-casting. Et il peut fonctionner pour les zones de chevauchement (intersections de soi), voir l'argument use_holes .
/* math lib (defined below) */
static float dot_v2v2(const float a[2], const float b[2]);
static float angle_signed_v2v2(const float v1[2], const float v2[2]);
static void copy_v2_v2(float r[2], const float a[2]);
/* intersection function */
bool isect_point_poly_v2(const float pt[2], const float verts[][2], const unsigned int nr,
const bool use_holes)
{
/* we do the angle rule, define that all added angles should be about zero or (2 * PI) */
float angletot = 0.0;
float fp1[2], fp2[2];
unsigned int i;
const float *p1, *p2;
p1 = verts[nr - 1];
/* first vector */
fp1[0] = p1[0] - pt[0];
fp1[1] = p1[1] - pt[1];
for (i = 0; i < nr; i++) {
p2 = verts[i];
/* second vector */
fp2[0] = p2[0] - pt[0];
fp2[1] = p2[1] - pt[1];
/* dot and angle and cross */
angletot += angle_signed_v2v2(fp1, fp2);
/* circulate */
copy_v2_v2(fp1, fp2);
p1 = p2;
}
angletot = fabsf(angletot);
if (use_holes) {
const float nested = floorf((angletot / (float)(M_PI * 2.0)) + 0.00001f);
angletot -= nested * (float)(M_PI * 2.0);
return (angletot > 4.0f) != ((int)nested % 2);
}
else {
return (angletot > 4.0f);
}
}
/* math lib */
static float dot_v2v2(const float a[2], const float b[2])
{
return a[0] * b[0] + a[1] * b[1];
}
static float angle_signed_v2v2(const float v1[2], const float v2[2])
{
const float perp_dot = (v1[1] * v2[0]) - (v1[0] * v2[1]);
return atan2f(perp_dot, dot_v2v2(v1, v2));
}
static void copy_v2_v2(float r[2], const float a[2])
{
r[0] = a[0];
r[1] = a[1];
}
Note: c'est l'une des méthodes les moins optimales car elle inclut beaucoup d'appels à atan2f , mais elle peut être d'intérêt pour les développeurs lisant ce thread (dans mes tests son ~23x plus lent alors en utilisant la méthode d'intersection de ligne).
pour détecter les impacts sur Polygon, nous devons tester deux choses:
- si le Point est à l'intérieur de la zone polygonale. (peut être réalisé par un algorithme de coulée de rayons)
- si le Point est à la limite du polygone(peut être accompli par le même algorithme qui est utilisé pour la détection de point sur le polyligne).
pour traiter les cas spéciaux suivants dans algorithme de moulage par rayons :
- le rayon chevauche un côté du polygone.
- Le point est à l'intérieur du polygone et le rayon passe par un sommet du polygone.
- Le point est à l'extérieur du polygone et le rayon touche un du polygone de l'angle.
Contrôle Pour Déterminer Si Un Point Est À L'Intérieur D'Un Polygone Complexe . L'article fournit un moyen facile de résoudre donc il n'y aura pas de traitement spécial requis pour le cas ci-dessus.
vous pouvez le faire en vérifiant si la zone formée en reliant le point désiré aux sommets de votre polygone correspond à la zone du polygone lui-même.
ou vous pouvez vérifier si la somme des angles intérieurs de votre point à chaque paire de deux sommets polygonaux consécutifs à votre point de contrôle se monte à 360, mais j'ai le sentiment que la première option est plus rapide parce qu'elle n'implique pas de divisions ni de calculs de l'inverse des fonctions trigonométriques.
Je ne sais pas ce qui se passe si votre polygone a un trou à l'intérieur mais il me semble que l'idée principale peut être adaptée à cette situation
vous pouvez aussi bien poster la question dans une communauté de mathématiques. Je parie qu'ils ont un million de façons de le faire
si vous cherchez une bibliothèque Java-script, il y a une extension v3 de google maps javascript pour la classe Polygon afin de détecter si un point y réside ou non.
var polygon = new google.maps.Polygon([], "#000000", 1, 1, "#336699", 0.3);
var isWithinPolygon = polygon.containsLatLng(40, -90);
en utilisant qt (Qt 4.3+), on peut utiliser la fonction de QPolygon containsPoint
la réponse dépend de si vous avez les polygones simples ou complexes. Les polygones simples ne doivent pas comporter d'intersections de segments de ligne. Donc ils peuvent avoir les trous mais les lignes ne peuvent pas se croiser. Les régions complexes peuvent avoir les intersections de ligne - de sorte qu'ils peuvent avoir les régions qui se chevauchent, ou les régions qui se touchent juste par un point unique.
pour les polygones simples, le meilleur algorithme est l'algorithme de moulage des rayons (nombre de croisement). Pour les polygones complexes, cet algorithme ne détecte pas les points à l'intérieur des régions qui se chevauchent. Ainsi, pour les polygones complexes, vous devez utiliser L'algorithme de nombres D'enroulement.
voici un excellent article avec une implémentation C des deux algorithmes. Je les ai essayés et ils fonctionnent bien.
version Scala de solution par nirg (suppose que le pré-contrôle rectangle limite est fait séparément):
def inside(p: Point, polygon: Array[Point], bounds: Bounds): Boolean = {
val length = polygon.length
@tailrec
def oddIntersections(i: Int, j: Int, tracker: Boolean): Boolean = {
if (i == length)
tracker
else {
val intersects = (polygon(i).y > p.y) != (polygon(j).y > p.y) && p.x < (polygon(j).x - polygon(i).x) * (p.y - polygon(i).y) / (polygon(j).y - polygon(i).y) + polygon(i).x
oddIntersections(i + 1, i, if (intersects) !tracker else tracker)
}
}
oddIntersections(0, length - 1, tracker = false)
}
j'ai fait une implémentation Python de nirg's c++ code :
Entrées
- bounding_points: noeuds qui composent le polygone.
-
bounding_box_positions: points candidats à filtrer. (Dans mon implémentation créé à partir de la boîte de limites.
(Les entrées sont des listes de tuples dans le format:
[(xcord, ycord), ...])
Renvoie
- tous les points à l'intérieur du polygone.
def polygon_ray_casting(self, bounding_points, bounding_box_positions):
# Arrays containing the x- and y-coordinates of the polygon's vertices.
vertx = [point[0] for point in bounding_points]
verty = [point[1] for point in bounding_points]
# Number of vertices in the polygon
nvert = len(bounding_points)
# Points that are inside
points_inside = []
# For every candidate position within the bounding box
for idx, pos in enumerate(bounding_box_positions):
testx, testy = (pos[0], pos[1])
c = 0
for i in range(0, nvert):
j = i - 1 if i != 0 else nvert - 1
if( ((verty[i] > testy ) != (verty[j] > testy)) and
(testx < (vertx[j] - vertx[i]) * (testy - verty[i]) / (verty[j] - verty[i]) + vertx[i]) ):
c += 1
# If odd, that means that we are inside the polygon
if c % 2 == 1:
points_inside.append(pos)
return points_inside
encore une fois, l'idée est tirée de ici
cela ne fonctionne que pour les formes convexes, mais le raffinement de portail Minkowski, et GJK sont également de grandes options pour tester si un point est dans un polygone. Vous utilisez minkowski soustraction pour soustraire le point du polygone, puis exécuter ces algorithmes pour voir si le polygone contient l'origine.
aussi, fait intéressant, vous pouvez décrire vos formes un peu plus implicitement en utilisant des fonctions de soutien qui prennent un vecteur de direction comme entrée et recracher le point le plus loin le long de ce vecteur. Cela vous permet de décrire toute forme convexe.. courbes, fait de polygones, ou mixte. Vous pouvez également effectuer des opérations pour combiner les résultats de fonctions de soutien simples pour faire des formes plus complexes.
plus d'information: http://xenocollide.snethen.com/mpr2d.html
aussi, game programming gems 7 parle de la façon de le faire en 3d (: