Comment puis-je calculer l'aire d'une courbe de bézier?
Étant donné le chemin suivant (par exemple) qui décrit une courbe de Bézier cubique SVG: "M300, 140C300,40,500,40,500,140", et en supposant une ligne droite reliant les points d'extrémité 300,140 à 500,140 (fermant l'aire sous la courbe), est-il possible de calculer l'aire ainsi fermée?
Quelqu'un peut-il Suggérer une formule (ou JavaScript) pour accomplir cela?
4 réponses
Convertir le tracé d'un polygone de précision arbitraire, puis calculer l'aire du polygone.
Démo Interactive: Zone de chemin par Subdivision
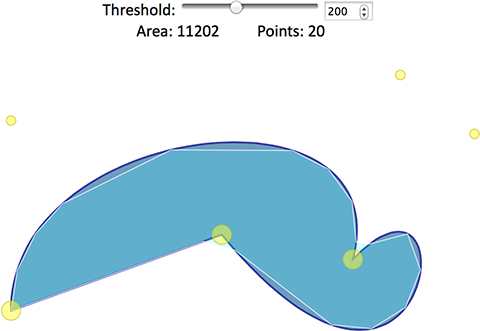
À la base, la démo ci-dessus utilise des fonctions pour subdiviser de manière adaptative path en un polygone et calculer l'aire d'un polygone :
// path: an SVG <path> element
// threshold: a 'close-enough' limit (ignore subdivisions with area less than this)
// segments: (optional) how many segments to subdivisions to create at each level
// returns: a new SVG <polygon> element
function pathToPolygonViaSubdivision(path,threshold,segments){
if (!threshold) threshold = 0.0001; // Get really, really close
if (!segments) segments = 3; // 2 segments creates 0-area triangles
var points = subdivide( ptWithLength(0), ptWithLength( path.getTotalLength() ) );
for (var i=points.length;i--;) points[i] = [points[i].x,points[i].y];
var doc = path.ownerDocument;
var poly = doc.createElementNS('http://www.w3.org/2000/svg','polygon');
poly.setAttribute('points',points.join(' '));
return poly;
// Record the distance along the path with the point for later reference
function ptWithLength(d) {
var pt = path.getPointAtLength(d); pt.d = d; return pt;
}
// Create segments evenly spaced between two points on the path.
// If the area of the result is less than the threshold return the endpoints.
// Otherwise, keep the intermediary points and subdivide each consecutive pair.
function subdivide(p1,p2){
var pts=[p1];
for (var i=1,step=(p2.d-p1.d)/segments;i<segments;i++){
pts[i] = ptWithLength(p1.d + step*i);
}
pts.push(p2);
if (polyArea(pts)<=threshold) return [p1,p2];
else {
var result = [];
for (var i=1;i<pts.length;++i){
var mids = subdivide(pts[i-1], pts[i]);
mids.pop(); // We'll get the last point as the start of the next pair
result = result.concat(mids)
}
result.push(p2);
return result;
}
}
// Calculate the area of an polygon represented by an array of points
function polyArea(points){
var p1,p2;
for(var area=0,len=points.length,i=0;i<len;++i){
p1 = points[i];
p2 = points[(i-1+len)%len]; // Previous point, with wraparound
area += (p2.x+p1.x) * (p2.y-p1.y);
}
return Math.abs(area/2);
}
}
// Return the area for an SVG <polygon> or <polyline>
// Self-crossing polys reduce the effective 'area'
function polyArea(poly){
var area=0,pts=poly.points,len=pts.numberOfItems;
for(var i=0;i<len;++i){
var p1 = pts.getItem(i), p2=pts.getItem((i+-1+len)%len);
area += (p2.x+p1.x) * (p2.y-p1.y);
}
return Math.abs(area/2);
}
Voici la réponse originale, qui utilise un autre technique (non adaptative) pour convertir le <path> en un <polygon>.
Démo Interactive: http://phrogz.net/svg/area_of_path.xhtml
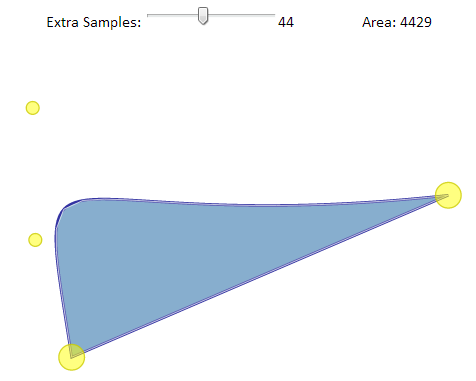
À la base, la démo ci-dessus utilise des fonctions pour approximer un chemin avec un polygone et calculer l'aire d'un polygone.
// Calculate the area of an SVG polygon/polyline
function polyArea(poly){
var area=0,pts=poly.points,len=pts.numberOfItems;
for(var i=0;i<len;++i){
var p1 = pts.getItem(i), p2=pts.getItem((i+len-1)%len);
area += (p2.x+p1.x) * (p2.y-p1.y);
}
return Math.abs(area/2);
}
// Create a <polygon> approximation for an SVG <path>
function pathToPolygon(path,samples){
if (!samples) samples = 0;
var doc = path.ownerDocument;
var poly = doc.createElementNS('http://www.w3.org/2000/svg','polygon');
// Put all path segments in a queue
for (var segs=[],s=path.pathSegList,i=s.numberOfItems-1;i>=0;--i)
segs[i] = s.getItem(i);
var segments = segs.concat();
var seg,lastSeg,points=[],x,y;
var addSegmentPoint = function(s){
if (s.pathSegType == SVGPathSeg.PATHSEG_CLOSEPATH){
}else{
if (s.pathSegType%2==1 && s.pathSegType>1){
x+=s.x; y+=s.y;
}else{
x=s.x; y=s.y;
}
var last = points[points.length-1];
if (!last || x!=last[0] || y!=last[1]) points.push([x,y]);
}
};
for (var d=0,len=path.getTotalLength(),step=len/samples;d<=len;d+=step){
var seg = segments[path.getPathSegAtLength(d)];
var pt = path.getPointAtLength(d);
if (seg != lastSeg){
lastSeg = seg;
while (segs.length && segs[0]!=seg) addSegmentPoint( segs.shift() );
}
var last = points[points.length-1];
if (!last || pt.x!=last[0] || pt.y!=last[1]) points.push([pt.x,pt.y]);
}
for (var i=0,len=segs.length;i<len;++i) addSegmentPoint(segs[i]);
for (var i=0,len=points.length;i<len;++i) points[i] = points[i].join(',');
poly.setAttribute('points',points.join(' '));
return poly;
}
J'ai hésité à faire un commentaire ou une réponse complète. Mais une simple recherche Google de "zone courbe de Bézier" se traduit par les trois premiers liens (le premier étant ce même poste), dans:
Http://objectmix.com/graphics/133553-area-closed-bezier-curve.html
Qui fournit la solution de forme fermée, en utilisant le théorème de divergence. Je suis surpris que ce lien n'ait pas été trouvé par L'OP.
Copier le texte dans le cas où le site tombe en panne, et créditer l'auteur de la réponse Kalle Rutanen:
Un problème intéressant. Pour toute courbe différentiable par morceaux en 2D, la procédure générale suivante vous donne la zone à l'intérieur de la courbe / série de courbes. Pour les courbes polynomiales (courbes de Bézier), vous obtiendrez solutions de forme fermée.
Soit G (t) une courbe différentiable par morceaux, avec 0
Soit F (x, y) = [x, y] / 2
Puis div (F (X, y)) = 1 où div est pour la divergence.
Maintenant, le théorème de divergence vous donne l'aire à l'intérieur de la courbe fermée g (t) comme une droite intégrale le long de la courbe:
Int(point(F(g(t)), perp(g'(t))) dt, t = 0..1) = (1 / 2) * int(point(g(t), perp(g'(t))) dt, t = 0..1)
Perp(x, y) = (-y, x)
Où int est pour l'intégration , ' pour la différenciation et dot pour dot produit. L'intégration doit être reconstituée aux pièces correspondantes aux segments de courbe lisses.
Maintenant pour des exemples. Prenez le degré Bézier 3 et une telle courbe avec les points de contrôle (x0, y0), (x1, y1), (x2, y2), (x3, y3). Intégrante sur cette courbe est:
I: = 3/10 * y1 * x0 - 3 / 20 * y1 * x2 - 3 / 20 * y1 * x3-3/10 * y0 * x1 - 3 / 20 * y0 * x2 - 1 / 20 * y0 * x3 + 3 / 20 * y2 * x0 + 3 / 20 * y2 * x1 - 3 / 10 * y2 * x3 + 1 / 20 * y3 * x0 + 3 / 20 * y3 * x1 + 3 / 10 * y3 * x2
Calculez ceci pour chaque courbe de la séquence et additionnez-les. Le somme est la zone délimitée par les courbes (en supposant que les courbes forment une boucle).
Si la courbe est constituée d'une seule courbe de Bézier, alors elle doit être x3 = x0 et y3 = y0, et l'aire est:
Zone: = 3/20 * y1 * x0 - 3 / 20 * y1 * x2 - 3 / 20 * y0 * x1 + 3 / 20 * y0 * x2 - 3 / 20 * y2 * x0 + 3 / 20 * y2 * x1
J'espère que je n'ai pas fait d'erreurs.
--
Kalle Rutanen
http://kaba.hilvi.org
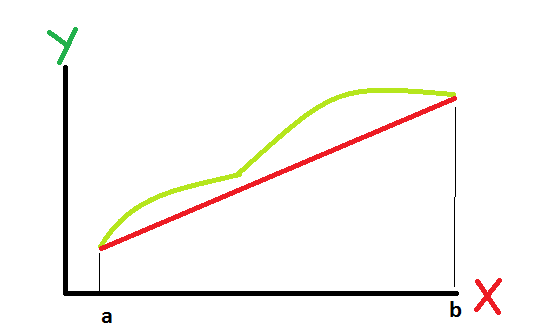
Tout d'abord, je ne suis pas si familier avec les courbes de Bézier, mais je sais que ce sont des fonctions continues. Si vous vous assurez que votre courbe cubique ne se croise pas, vous pouvez l'intégrer sous forme fermée (je veux dire en utilisant des intégrales analytiques)sur le domaine englobant donné ([a-b]) et soustraire la zone du triangle formée par l'extrémité joignant la ligne droite et l'axe X. En cas d'intersection avec la courbe de Bézier et l'extrémité joignant la ligne droite, vous pouvez diviser en sections et essayer de calculer chaque zone séparément d'une manière cohérente..
Pour moi, les termes de recherche appropriés sont "intégration de fonction continue" "intégrales" "zone sous une fonction" "Calcul"
Bien sûr, vous pouvez générer des données discrètes à partir de votre courbe de Bézier fn et obtenir des données x-y discrètes et calculer l'intégrale approximativement.
J'aime la solution dans la réponse acceptée par Phrogz, mais j'ai aussi regardé un peu plus loin et j'ai trouvé un moyen de faire la même chose avec du papier.js utilisant la classe CompoundPath et la propriété area. Voir mon article.js démo.
Le résultat (surface area = 11856) est exactement le même qu'avec la démo de Phrogz lors de l'utilisation du seuil 0, mais le traitement semble beaucoup plus rapide! Je sais que c'est exagéré de charger du papier.js juste pour calculer la surface, mais si vous envisagez de mettre en œuvre un cadre ou envie d'enquêter sur la façon dont le papier.js le fait...