Algorithme de l'escalade des collines exemple simple
je suis un peu confus avec l'Escalade de l'algorithme. Je veux "exécuter "l'algorithme jusqu'à ce que je trouve la première solution dans cet arbre ("a" est initial et h et k sont des états finaux ) et il dit que les nombres près des États sont les valeurs heuristiques. Voici l'arborescence:
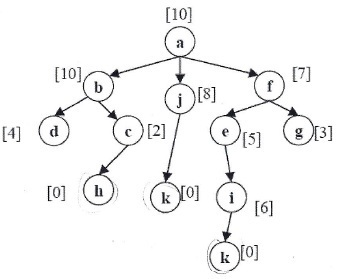
ma question : je suis en train de lancer l'escalade sur l'arbre, alors ok, nous commençons a-> f-> g et puis quoi ??finition(sans résultat) , mais j'ai lu que l'escalade peut pas revenir en arrière et faire un nouveau choix(exemple j ou e) ? Est-ce exact ? Si je peux y retourner alors comment ? je veux dire, lorsque nous changeons notre exemple de choix initial, nous choisissons e au lieu de g ou j au lieu de f
Désolé si ma question est trop simple .
7 réponses
une façon courante d'éviter de se coincer dans les maxima locaux avec L'escalade de Colline est d'utiliser des redémarrages aléatoires. Dans votre exemple si G est une maxima locale, l'algorithme s'arrêterait là et choisirait alors un autre noeud aléatoire pour le redémarrer. Donc si J ou C ont été choisis (ou peut-être A, B, Ou D) vous trouverez les maxima globaux en H ou K. rincez et répétez assez de fois et vous trouverez les maxima globaux ou quelque chose de proche; en fonction du temps/ressources limites et l'espace de problème.
Note cette recherche locale comme L'escalade de Colline n'est pas complète et ne peut pas garantir de trouver la maxima globale. L'avantage, bien sûr, est qu'il ne nécessite qu'une fraction des ressources. Dans la pratique et appliquée aux bons problèmes, c'est une solution très efficace.
Vous pouvez essayer d'utiliser une technique appelée simulation de recuit pour empêcher votre recherche de rester collée sur les minimums locaux. Essentiellement, dans un recuit simulé, il y a un paramètre T qui contrôle votre Probabilité de passer à des états de voisinage sous-optimaux. Si T est élevé, vous êtes plus susceptible de faire un déplacement sous-optimal vers un État voisin et pourrait ainsi échapper à un minimum local lorsque coincé là, ce que vous ne le feriez pas si vous avez utilisé la colline normale escalade.
l'escalade N'a aucune garantie contre le risque de rester bloqué dans un minimum/maximum local. Cependant, seule la forme la plus pure de l'escalade ne vous permet pas de faire marche arrière.
un simple riff sur l'escalade de colline qui évitera la question des minima locaux (au détriment de plus de temps et de mémoire) est une recherche tabu, où vous vous souvenez des mauvais résultats antérieurs et volontairement les éviter.
l'un des problèmes avec l'escalade de colline est de se coincer aux minima locaux et c'est ce qui se passe quand vous atteignez F. une version améliorée de l'escalade de colline (qui est en fait utilisé pratiquement) est de redémarrer l'ensemble du processus en sélectionnant un noeud aléatoire dans l'arbre de recherche et de continuer à trouver une solution optimale. Si une fois de plus vous êtes coincé à certains minima locaux, vous devez redémarrer à nouveau avec un autre nœud aléatoire. En général, il y a une limite sur le non. du temps tu peux le refaire ce processus de trouver la solution optimale. Après avoir atteint cette limite, vous sélectionnez le moins parmi tous les minima locaux que vous avez atteints au cours du processus. Bien qu'il ne soit pas encore complet, mais celui-ci a de meilleures chances de trouver la solution globale optimale.
en fait, en escaladant une colline, vous ne reculez généralement pas, parce que vous ne gardez pas la trace de l'état (c'est la recherche locale) et vous vous éloignez d'un maxima. Ni le retour en arrière, ni la recherche de Tabu n'aident à répondre à la question: le premier vous éloigne simplement d'une maxima locale et le second vous empêche de revisiter la même maxima locale. Ni vous aider à frapper un mondial des maxima. - Tyson Oct 16 ' 12 à 22: 59
" où vous vous souvenez de mauvais résultats antérieurs et Je ne peux pas être d'accord, vous marquez comme tabou aussi de bonnes solutions, mais vous ne voulez pas suivre la même voie à nouveau. –
Voici la solution:
A - > F, avec le moindre coût possible F -> G avec le coût 3 mais il n'y a pas de chemin.
redémarrez à partir du moindre coût possible autre que G, Eh bien C'est E parce que E a déjà été inséré dans la file d'attente/pile/file de priorité ou quelle que soit la structure de données que vous utilisez.
donc E - > I mais j'ai un coût plus élevé que E donc vous êtes coincé: S
redémarrer à partir du moindre coût autre que F E & G, donc nous choisissons J parce que J a un coût plus faible que B avec une différence de 2 i.e. J = 8 B = 10
J - > K avec cost 0 ainsi K est le but
NOTE: la variante proposée de l'escalade de colline pour choisir un point au hasard, mais choisir le moindre coût autre que les noeuds déjà visités est mieux que de choisir au hasard.
une autre NOTE: est que lorsque le noeud E n'a pas visité I parce que j'ai une valeur plus élevée que E, l'algorithme l'a déjà inséré dans la structure de données, choisissant ainsi le moindre coût autre que le déjà visité créerait un nouveau chemin à partir de I parce que je n'ai jamais été visité et donc il a une valeur inférieure à J, c'est le seul chemin que j'ai sauté.
le chemin selon la montée pure sera a - > J - > k si vous développez les enfants de gauche à droite, si vous les développez de droite à gauche, vous obtiendrez les minima locaux A - > F - > G, mais en général, nous nous étendons de gauche à droite.