Région de densité postérieure la plus élevée et région centrale crédible
étant donné un p postérieur (Θ / D) sur certains paramètres Θ, on peut définir le code suivant:
Région De Densité Postérieure La Plus Élevée:
Région De Densité Postérieure La Plus Élevée est l'ensemble des valeurs les plus probables de Θ qui, au total, constituent 100(1-α) % de la masse postérieure.
En d'autres termes, pour un α, nous recherchons un *p** satisfait:
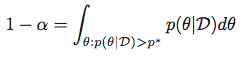
et puis obtenir le Région De Densité Postérieure La Plus Élevée le jeu:
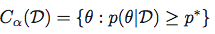
Région Centrale Crédible:
en Utilisant la même notation que ci-dessus, une région crédible (ou intervalle) est défini comme suit:
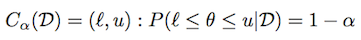
selon la distribution, il pourrait y avoir beaucoup de tels intervalles. La centrale crédible intervalle est défini comme un intervalle crédible où il est (1-α) / 2 masse queue.
Calcul:
pour les distributions générales, étant donné les échantillons de la distribution, y a-t-il des entrées pour obtenir les deux quantités ci-dessus en Python ou PyMC<!--8?
pour les distributions paramétriques communes (par ex. bêta, gaussien, etc.) y a-t-il des bibliothèques ou des bibliothèques intégrées pour calculer ceci en utilisant SciPy ou statsmodels?
6 réponses
pour calculer HPD vous pouvez utiliser pymc3, voici un exemple
import pymc3
from scipy.stats import norm
a = norm.rvs(size=10000)
pymc3.stats.hpd(a)
d'après ce que j'ai compris, "région centrale crédible" n'est pas différent de la façon dont les intervalles de confiance sont calculés; tout ce dont vous avez besoin est l'inverse de cdf function alpha/2 et 1-alpha/2;scipy c'est ppf (fonction du point de pourcentage); ainsi que pour la distribution postérieure gaussienne:
>>> from scipy.stats import norm
>>> alpha = .05
>>> l, u = norm.ppf(alpha / 2), norm.ppf(1 - alpha / 2)
pour vérifier que [l, u] couvre (1-alpha) postérieure densité:
>>> norm.cdf(u) - norm.cdf(l)
0.94999999999999996
de même pour la bêta postérieure avec say a=1 et b=3:
>>> from scipy.stats import beta
>>> l, u = beta.ppf(alpha / 2, a=1, b=3), beta.ppf(1 - alpha / 2, a=1, b=3)
et aussi:
>>> beta.cdf(u, a=1, b=3) - beta.cdf(l, a=1, b=3)
0.94999999999999996
ici vous pouvez voir les distributions paramétriques qui sont incluses dans scipy; et je suppose que toutes ont ppf;
quant à la région de densité postérieure la plus élevée, elle est plus délicate, puisque pdf fonction n'est pas nécessairement inversible; et en général une telle région ne peut même pas être connectée; par exemple, dans le cas de bêta avec a = b = .5 ( comme on peut le voir ici);
mais, dans le cas de la distribution gaussienne, il est facile de voir que la "région de densité postérieure la plus élevée" coïncide avec la "région centrale crédible"; et je pense que c'est le cas pour toutes les distributions unimodales symétriques ( i.e. si la fonction pdf est symétrique autour du mode de distribution)
une approche numérique possible pour le cas général serait une recherche binaire sur la valeur de p* en utilisant intégration numérique pdf en utilisant le fait que l'intégrale est une fonction monotone de p*;
Voici un exemple de mélange Gaussien:
[1] la première chose dont vous avez besoin est une fonction PDF analytique; pour mélange gaussien qui est facile:
def mix_norm_pdf(x, loc, scale, weight):
from scipy.stats import norm
return np.dot(weight, norm.pdf(x, loc, scale))
ainsi par exemple pour les valeurs de localisation, de balance et de poids comme dans
loc = np.array([-1, 3]) # mean values
scale = np.array([.5, .8]) # standard deviations
weight = np.array([.4, .6]) # mixture probabilities
vous obtiendrez deux belles distributions gaussiennes mains:
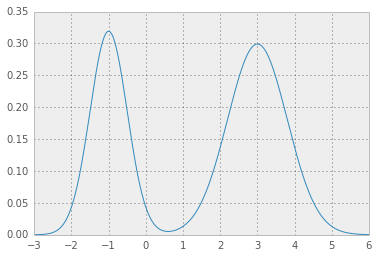
[2] maintenant, vous avez besoin d'une fonction d'erreur qui donné une valeur de test pour p* intègre la fonction pdf ci-dessus p* et renvoie l'erreur quadratique de la valeur désirée 1 - alpha:
def errfn( p, alpha, *args):
from scipy import integrate
def fn( x ):
pdf = mix_norm_pdf(x, *args)
return pdf if pdf > p else 0
# ideally integration limits should not
# be hard coded but inferred
lb, ub = -3, 6
prob = integrate.quad(fn, lb, ub)[0]
return (prob + alpha - 1.0)**2
[3] maintenant, pour une valeur donnée de alpha nous pouvons minimiser la fonction d'erreur pour obtenir p*:
alpha = .05
from scipy.optimize import fmin
p = fmin(errfn, x0=0, args=(alpha, loc, scale, weight))[0]
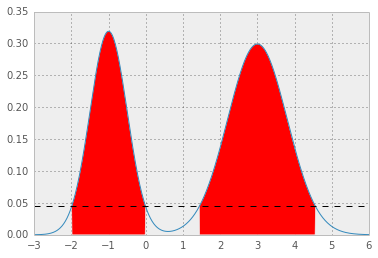
résultats p* = 0.0450, et HPD comme ci-dessous; la zone rouge représente 1 - alpha de la distribution, et la ligne pointillée horizontale est p*.
PyMC a une fonction intégrée pour le calcul du hpd. En v2.3 c'est dans utils. Voir la source ici. Comme exemple d'un modèle linéaire et C'est HPD
import pymc as pc
import numpy as np
import matplotlib.pyplot as plt
## data
np.random.seed(1)
x = np.array(range(0,50))
y = np.random.uniform(low=0.0, high=40.0, size=50)
y = 2*x+y
## plt.scatter(x,y)
## priors
emm = pc.Uniform('m', -100.0, 100.0, value=0)
cee = pc.Uniform('c', -100.0, 100.0, value=0)
#linear-model
@pc.deterministic(plot=False)
def lin_mod(x=x, cee=cee, emm=emm):
return emm*x + cee
#likelihood
llhy = pc.Normal('y', mu=lin_mod, tau=1.0/(10.0**2), value=y, observed=True)
linearModel = pc.Model( [llhy, lin_mod, emm, cee] )
MCMClinear = pc.MCMC( linearModel)
MCMClinear.sample(10000,burn=5000,thin=5)
linear_output=MCMClinear.stats()
## pc.Matplot.plot(MCMClinear)
## print HPD using the trace of each parameter
print(pc.utils.hpd(MCMClinear.trace('m')[:] , 1.- 0.95))
print(pc.utils.hpd(MCMClinear.trace('c')[:] , 1.- 0.95))
Vous pouvez également envisager de calculer les quantiles
print(linear_output['m']['quantiles'])
print(linear_output['c']['quantiles'])
où je pense que si vous prenez juste les valeurs de 2,5% à 97,5%, vous obtenez votre intervalle de crédibilité de 95%.
une autre option (adaptée de R à Python) et tirée du livre Doing bayesian data analysis de John K. Kruschke) est la suivante:
from scipy.optimize import fmin
from scipy.stats import *
def HDIofICDF(dist_name, credMass=0.95, **args):
# freeze distribution with given arguments
distri = dist_name(**args)
# initial guess for HDIlowTailPr
incredMass = 1.0 - credMass
def intervalWidth(lowTailPr):
return distri.ppf(credMass + lowTailPr) - distri.ppf(lowTailPr)
# find lowTailPr that minimizes intervalWidth
HDIlowTailPr = fmin(intervalWidth, incredMass, ftol=1e-8, disp=False)[0]
# return interval as array([low, high])
return distri.ppf([HDIlowTailPr, credMass + HDIlowTailPr])
L'idée est de créer une fonction intervalWidth que retourne la largeur de l'intervalle de commence à lowTailPr et a credMass masse. Le minimum de la fonction intervalWidth est fondé en utilisant fmin minimiseur de scipy.
Par exemple le résultat de:
print HDIofICDF(norm, credMass=0.95, loc=0, scale=1)
[-1.95996398 1.95996398]
le nom des paramètres de distribution passés à HDIofICDF, doit être exactement le même que celui utilisé en scipy.
je suis tombé sur ce post en essayant de trouver un moyen d'estimer un IDH à partir d'un échantillon MCMC mais aucune des réponses n'a fonctionné pour moi. Comme aloctavodia, j'ai adapté à Python un exemple R du livre Doing Bayesian Data Analysis. J'avais besoin de calculer un IDH de 95% à partir d'un échantillon MCMC. Voici ma solution:
import numpy as np
def HDI_from_MCMC(posterior_samples, credible_mass):
# Computes highest density interval from a sample of representative values,
# estimated as the shortest credible interval
# Takes Arguments posterior_samples (samples from posterior) and credible mass (normally .95)
sorted_points = sorted(posterior_samples)
ciIdxInc = np.ceil(credible_mass * len(sorted_points)).astype('int')
nCIs = len(sorted_points) - ciIdxInc
ciWidth = [0]*nCIs
for i in range(0, nCIs):
ciWidth[i] = sorted_points[i + ciIdxInc] - sorted_points[i]
HDImin = sorted_points[ciWidth.index(min(ciWidth))]
HDImax = sorted_points[ciWidth.index(min(ciWidth))+ciIdxInc]
return(HDImin, HDImax)
La méthode ci-dessus me donne des réponses logiques basées sur les données que j'ai!
vous pouvez obtenir l'intervalle central crédible de deux façons: graphiquement, quand vous appelez summary_plot sur les variables de votre modèle, il y a un bpd drapeau est réglé sur True par défaut. La modification de cette False dessinera les intervalles centraux. La deuxième lieu, il est lorsque vous appelez l' summary méthode sur votre modèle ou un noeud; il vous donnera des quantiles postérieurs, et les externes seront 95% intervalle central par défaut (que vous pouvez changer avec le alpha argument.)