Interpolation locale d'ordre supérieur des courbes implicites en Python

étant donné un ensemble de points décrivant une certaine trajectoire dans le plan 2D, je voudrais fournir une représentation en douceur de cette trajectoire avec une interpolation locale de haut ordre.

par exemple, disons que nous définissons un cercle en 2D avec 11 points dans la figure ci-dessous. Je voudrais ajouter des points entre chaque paire consécutive de points dans l'ordre ou produire une trace lisse. Ajouter des points sur chaque segment est assez facile, mais il produit des discontinuités de pente typique pour un le local "interpolation linéaire". Bien sûr, il n'est pas une interpolation dans le sens classique, parce que

• la fonction peut avoir des valeurs multiples y pour un x
• ajouter simplement plus de points sur la trajectoire serait très bien (aucune représentation continue n'est nécessaire).

donc je ne sais pas quel serait le vocabulaire approprié pour cela.

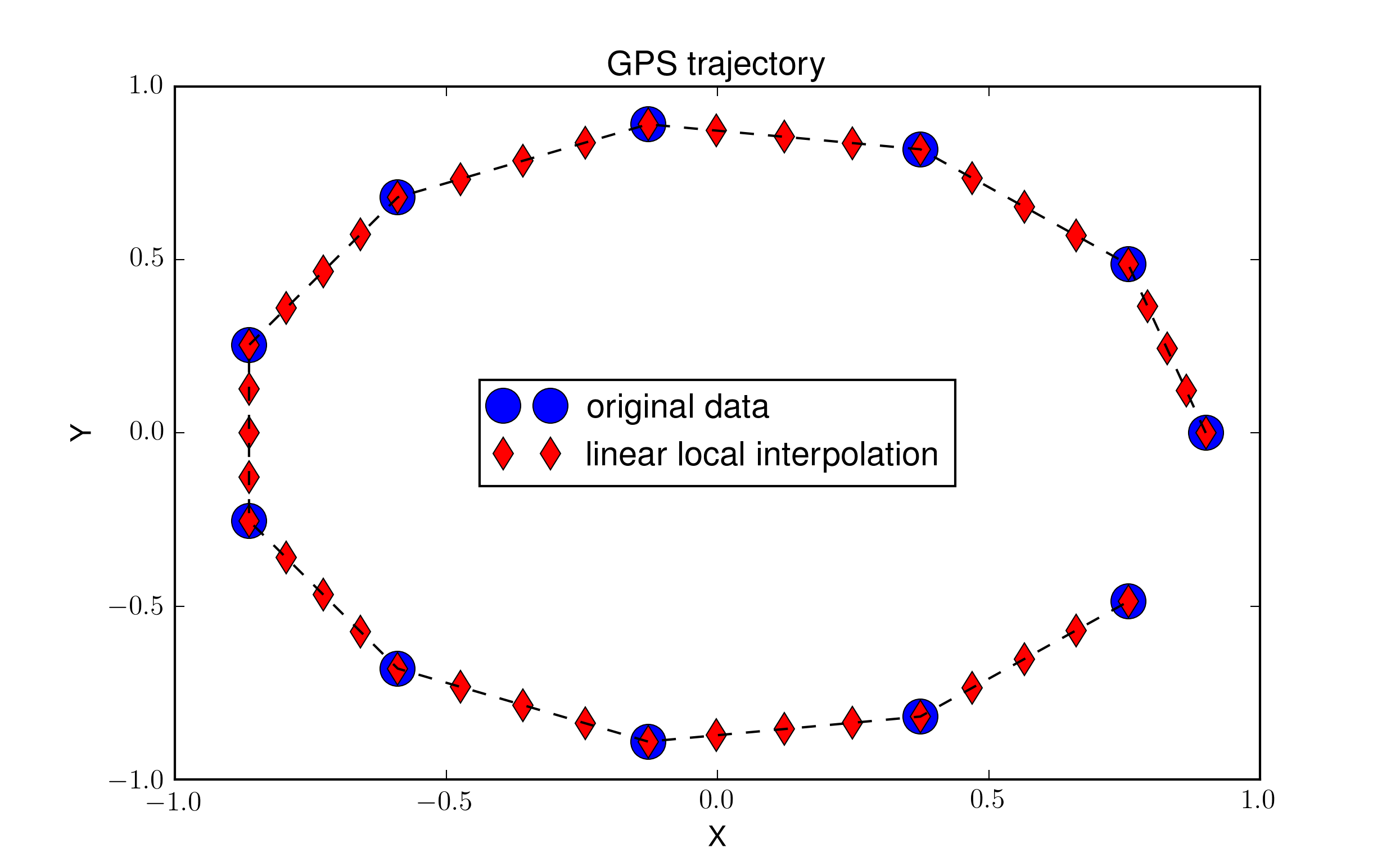
le code pour produire cette figure se trouve ci-dessous. L'interpolation linéaire est réalisée avec la fonction lin_refine_implicit . Je suis à la recherche d'une solution d'ordre supérieur pour produire une trace lisse et je me demandais s'il y a un moyen de l'atteindre avec des fonctions classiques en Scipy? J'ai essayé d'utiliser diverses interpolations 1D de scipy.interpolate sans grand succès (encore une fois à cause de multiples y valeurs pour un x donné ).

le but final est d'utiliser cette méthode pour fournir une trajectoire GPS lisse à partir de mesures discrètes, donc je pense que cela devrait avoir une solution classique quelque part.

import numpy as np
import matplotlib.pyplot as plt

def lin_refine_implicit(x, n):
    """
    Given a 2D ndarray (npt, m) of npt coordinates in m dimension, insert 2**(n-1) additional points on each trajectory segment
    Returns an (npt*2**(n-1), m) ndarray
    """
    if n > 1:
        m = 0.5*(x[:-1] + x[1:])
        if x.ndim == 2:
            msize = (x.shape[0] + m.shape[0], x.shape[1])
        else:
            raise NotImplementedError

        x_new = np.empty(msize, dtype=x.dtype)
        x_new[0::2] = x
        x_new[1::2] = m
        return lin_refine_implicit(x_new, n-1)
    elif n == 1:
        return x
    else:
        raise ValueError
n = 11
r = np.arange(0, 2*np.pi, 2*np.pi/n)
x = 0.9*np.cos(r)
y = 0.9*np.sin(r)
xy = np.vstack((x, y)).T
xy_highres_lin = lin_refine_implicit(xy, n=3)

plt.plot(xy[:,0], xy[:,1], 'ob', ms=15.0, label='original data')
plt.plot(xy_highres_lin[:,0], xy_highres_lin[:,1], 'dr', ms=10.0, label='linear local interpolation')
plt.legend(loc='best')
plt.plot(x, y, '--k')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('GPS trajectory')
plt.show()