Coordonnées Du Quadrillage Hexagonal En Pixels
je travaille avec une grille hexagonale. J'ai choisi d'utiliser ce système de coordonnées, car il est très élégant.
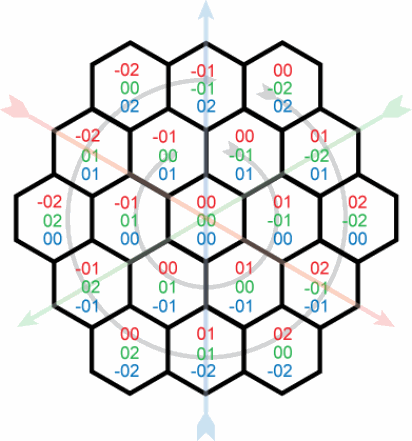
Cette question parle de générer les coordonnées eux-mêmes, et est très utile. Mon problème maintenant est de convertir ces coordonnées et réelle des coordonnées en pixels. Je cherche un moyen simple de trouver le centre d'un hexagone avec les coordonnées x,y,Z. Supposons (0,0) en coordonnées pixel est à (0,0) en hexagones, et que chaque hexagone a un bord de longueur S. Il me semble que x, y, et z devraient chacun déplacer ma coordonnée une certaine distance le long d'un axe, mais ils sont interdépendants d'une manière étrange Je ne peux pas tout à fait envelopper ma tête autour de lui.
points Bonus si vous pouvez aller dans l'autre direction et convertir n'importe quel (x,y) point en coordonnées pixel à l'hexagone que le point appartient.
1 réponses
pour plus de clarté, que les coordonnées" hexagonales "soient (r,g,b) où r , g , et b sont les coordonnées rouge , Vert , et bleu , respectivement. Les coordonnées (r,g,b) et (x,y) sont liées par ce qui suit:
y = 3/2 * s * b
b = 2/3 * y / s
x = sqrt(3) * s * ( b/2 + r)
x = - sqrt(3) * s * ( b/2 + g )
r = (sqrt(3)/3 * x - y/3 ) / s
g = -(sqrt(3)/3 * x + y/3 ) / s
r + b + g = 0
Dérivation:
-
j'ai d'abord remarquez que n'importe quelle rangée horizontale d'hexagones (qui devrait avoir une constante
y-coordonnée) avait une constantebcoordonnée, doncydépendait seulement deb. Chaque hexagone peut être divisé en six triangles équilatéraux avec les côtés de la longueurs; les centres des hexagones dans une rangée sont un et demi-longueurs de côté au-dessus / au-dessous des centres dans la rangée suivante (ou, peut-être plus facile à voir, les centres dans une rangée sont 3 longueurs de côté au-dessus/au-dessous des centres deux rows away), donc pour chaque changement de1dansb,ychange3/2 * s, donnant la première formule. La résolution pourben termes deydonne la deuxième formule. -
les hexagones avec une coordonnée donnée
ront tous des centres sur une ligne perpendiculaire à l'axe r au point sur l'axerqui est3/2 * sde l'origine (similaire à la dérivation ci-dessus deyen termes deb). L'axera la pente-sqrt(3)/3, ainsi une ligne perpendiculaire à elle a la pentesqrt(3); le point sur l'axeret sur la ligne a les coordonnées(3sqrt(3)/4 * s * r, -3/4 * s * r); ainsi une équation dansxetypour la ligne contenant les centres des hexagones avecr- coordonnéeresty + 3/4 * s * r = sqrt(3) * (x - 3sqrt(3)/4 * s * r). La substitution deypar la première formule et la résolution dexdonne la deuxième formule. (Ce n'est pas comme ça que j'ai dérivé celle-ci, mais ma dérivation était graphique avec beaucoup d'essais et d'erreurs et cette méthode algébrique est plus concise.) -
l'ensemble des hexagones avec une coordonnée donnée
rest la réflexion horizontale de l'ensemble des hexagones avec cette coordonnée g, donc quelle que soit la formule pour la coordonnéexen termes deretb, la coordonnéexpour cette formule avecgau lieu dersera l'inverse. Cela donne la troisième formule. -
les quatrième et cinquième formules proviennent de la substitution de la deuxième formule pour
bet de la résolution pourrougen termes dexety. -
la formule finale est venue de l'observation, vérifiée par l'algèbre avec les formules précédentes.