Étant donné le nombre premier N, calculer le premier suivant?

il y a environ un an, je travaillais dans ce domaine pour libc++ tout en mettant en œuvre le conteneurs non classés (hachés) pour C++11. Je pensais que je voudrais partager mes expériences ici. Cette expérience soutient réponse acceptée de marcog pour un raisonnable définition de"force brute".

cela signifie que même une simple force brute sera assez rapide dans la plupart des les circonstances, en prenant O(ln (p)*sqrt (p)) en moyenne.

j'ai développé plusieurs implémentations de size_t next_prime(size_t n) où le spec de cette fonction est:

retourne: le plus petit prime qui est supérieur ou égal à n .

chaque mise en œuvre de next_prime est accompagnée d'une fonction d'aide is_prime . is_prime devrait être considéré comme un privé détail de la mise en œuvre; ne doit pas être appelé directement par le client. Chacune de ces implémentations a bien sûr été testée pour sa justesse, mais aussi testé avec l'essai de performance suivant:

int main()
{
    typedef std::chrono::high_resolution_clock Clock;
    typedef std::chrono::duration<double, std::milli> ms;
    Clock::time_point t0 = Clock::now();

    std::size_t n = 100000000;
    std::size_t e = 100000;
    for (std::size_t i = 0; i < e; ++i)
        n = next_prime(n+1);

    Clock::time_point t1 = Clock::now();
    std::cout << e/ms(t1-t0).count() << " primes/millisecond\n";
    return n;
}

je dois souligner qu'il s'agit d'un test de performance, et ne reflète pas typique d'utilisation, qui ressemblerait plus à:

// Overflow checking not shown for clarity purposes
n = next_prime(2*n + 1);

tous les essais de performance ont été compilés avec:

clang++ -stdlib=libc++ -O3 main.cpp

Mise en œuvre 1

il y a sept implémentations. Le but de l'affichage du premier mise en œuvre est de démontrer que si vous ne parvenez pas à arrêter de tester le candidat prime x pour les facteurs à sqrt(x) alors vous avez même pas réussi à atteindre un une mise en œuvre qui pourrait être qualifiée de force brutale. Cette mise en œuvre est brutalement lent .

bool
is_prime(std::size_t x)
{
    if (x < 2)
        return false;
    for (std::size_t i = 2; i < x; ++i)
    {
        if (x % i == 0)
            return false;
    }
    return true;
}

std::size_t
next_prime(std::size_t x)
{
    for (; !is_prime(x); ++x)
        ;
    return x;
}

pour cette mise en œuvre seulement J'ai dû mettre e à 100 au lieu de 100000, juste pour obtenez une durée de fonctionnement raisonnable:

0.0015282 primes/millisecond

"1519560920 la mise en Œuvre" 2

cette mise en œuvre est la plus lente de la brute force la seule différence par rapport à l'implémentation 1 est qu'elle cesse les tests de primeness lorsque le facteur dépasse sqrt(x) .

bool
is_prime(std::size_t x)
{
    if (x < 2)
        return false;
    for (std::size_t i = 2; true; ++i)
    {
        std::size_t q = x / i;
        if (q < i)
            return true;
        if (x % i == 0)
            return false;
    }
    return true;
}

std::size_t
next_prime(std::size_t x)
{
    for (; !is_prime(x); ++x)
        ;
    return x;
}

noter que sqrt(x) n'est pas calculé directement, mais déduit par q < i . Ce accélère les choses d'un facteur de milliers:

5.98576 primes/millisecond

et valide la prédiction de marcog:

... c'est bien dans les limites de la plupart des problèmes en prenant sur l'ordre de une milliseconde sur le matériel le plus moderne.

"1519560920 la mise en Œuvre" 3

on peut près du double de la vitesse (au moins sur le matériel que j'utilise) par éviter l'utilisation de l'opérateur % :

bool
is_prime(std::size_t x)
{
    if (x < 2)
        return false;
    for (std::size_t i = 2; true; ++i)
    {
        std::size_t q = x / i;
        if (q < i)
            return true;
        if (x == q * i)
            return false;
    }
    return true;
}

std::size_t
next_prime(std::size_t x)
{
    for (; !is_prime(x); ++x)
        ;
    return x;
}

11.0512 primes/millisecond

"1519560920 la mise en Œuvre" 4

jusqu'à présent je n'ai même pas utilisé la connaissance commune que 2 est le seul même premier. Cette mise en œuvre incorpore cette connaissance, doublant presque la vitesse encore une fois:

bool
is_prime(std::size_t x)
{
    for (std::size_t i = 3; true; i += 2)
    {
        std::size_t q = x / i;
        if (q < i)
            return true;
        if (x == q * i)
            return false;
    }
    return true;
}

std::size_t
next_prime(std::size_t x)
{
    if (x <= 2)
        return 2;
    if (!(x & 1))
        ++x;
    for (; !is_prime(x); x += 2)
        ;
    return x;
}

21.9846 primes/millisecond

mise en oeuvre 4 est probablement ce que la plupart des gens ont à l'esprit quand ils pensent "brute force".

"1519560920 la mise en Œuvre" 5

en utilisant la formule suivante, vous pouvez facilement choisir tous les numéros qui sont divisible par Ni 2 Ni 3:

6 * k + {1, 5}

où k >= 1. La mise en œuvre suivante utilise cette formule, mais mise en œuvre avec un tour de xor mignon:

bool
is_prime(std::size_t x)
{
    std::size_t o = 4;
    for (std::size_t i = 5; true; i += o)
    {
        std::size_t q = x / i;
        if (q < i)
            return true;
        if (x == q * i)
            return false;
        o ^= 6;
    }
    return true;
}

std::size_t
next_prime(std::size_t x)
{
    switch (x)
    {
    case 0:
    case 1:
    case 2:
        return 2;
    case 3:
        return 3;
    case 4:
    case 5:
        return 5;
    }
    std::size_t k = x / 6;
    std::size_t i = x - 6 * k;
    std::size_t o = i < 2 ? 1 : 5;
    x = 6 * k + o;
    for (i = (3 + o) / 2; !is_prime(x); x += i)
        i ^= 6;
    return x;
}

Cela signifie que l'algorithme doit vérifier seulement 1/3 de le nombres entiers pour primeness au lieu de la moitié des nombres et le test de performance montre l'accélération attendue de près de 50%:

32.6167 primes/millisecond

"1519560920 la mise en Œuvre" 6

cette implémentation est une extension logique de l'implémentation 5: elle utilise les formule suivante pour calculer tous les nombres qui ne sont pas divisibles par 2, 3 et 5:

30 * k + {1, 7, 11, 13, 17, 19, 23, 29}

il décompose également la boucle interne dans is_prime, et crée une liste de "petit primes " qui est utile pour traiter les numéros de moins de 30.

static const std::size_t small_primes[] =
{
    2,
    3,
    5,
    7,
    11,
    13,
    17,
    19,
    23,
    29
};

static const std::size_t indices[] =
{
    1,
    7,
    11,
    13,
    17,
    19,
    23,
    29
};

bool
is_prime(std::size_t x)
{
    const size_t N = sizeof(small_primes) / sizeof(small_primes[0]);
    for (std::size_t i = 3; i < N; ++i)
    {
        const std::size_t p = small_primes[i];
        const std::size_t q = x / p;
        if (q < p)
            return true;
        if (x == q * p)
            return false;
    }
    for (std::size_t i = 31; true;)
    {
        std::size_t q = x / i;
        if (q < i)
            return true;
        if (x == q * i)
            return false;
        i += 6;

        q = x / i;
        if (q < i)
            return true;
        if (x == q * i)
            return false;
        i += 4;

        q = x / i;
        if (q < i)
            return true;
        if (x == q * i)
            return false;
        i += 2;

        q = x / i;
        if (q < i)
            return true;
        if (x == q * i)
            return false;
        i += 4;

        q = x / i;
        if (q < i)
            return true;
        if (x == q * i)
            return false;
        i += 2;

        q = x / i;
        if (q < i)
            return true;
        if (x == q * i)
            return false;
        i += 4;

        q = x / i;
        if (q < i)
            return true;
        if (x == q * i)
            return false;
        i += 6;

        q = x / i;
        if (q < i)
            return true;
        if (x == q * i)
            return false;
        i += 2;
    }
    return true;
}

std::size_t
next_prime(std::size_t n)
{
    const size_t L = 30;
    const size_t N = sizeof(small_primes) / sizeof(small_primes[0]);
    // If n is small enough, search in small_primes
    if (n <= small_primes[N-1])
        return *std::lower_bound(small_primes, small_primes + N, n);
    // Else n > largest small_primes
    // Start searching list of potential primes: L * k0 + indices[in]
    const size_t M = sizeof(indices) / sizeof(indices[0]);
    // Select first potential prime >= n
    //   Known a-priori n >= L
    size_t k0 = n / L;
    size_t in = std::lower_bound(indices, indices + M, n - k0 * L) - indices;
    n = L * k0 + indices[in];
    while (!is_prime(n))
    {
        if (++in == M)
        {
            ++k0;
            in = 0;
        }
        n = L * k0 + indices[in];
    }
    return n;
}

c'est sans doute au-delà de la "force brute" et est bon pour stimuler la la vitesse de l'autre de 27,5% pour:

41.6026 primes/millisecond

"1519560920 la mise en Œuvre" 7

C'est pratique pour jouer la partie pour une itération, le développement d'une formule pour les nombres non divisibles par 2, 3, 5 et 7:

210 * k + {1, 11, ...},

le code source n'est pas montré ici, mais est très similaire à l'implémentation 6. C'est l'implémentation que j'ai choisi d'utiliser pour les conteneurs non classés de libc++ , et que le code source est open source (trouvé sur le lien).

cette dernière itération est bonne pour une autre augmentation de vitesse de 14,6% à:

47.685 primes/millisecond

L'utilisation de cet algorithme assure que les clients de libc++ 's tables de hachage peuvent choisir toute prime qu'ils décident est le plus bénéfique à leur situation, et la performance pour cette application est tout à fait acceptable.

Juste au cas où quelqu'un est curieux:

utilisant réflecteur j'ai déterminé que .Net utilise une classe statique qui contient une liste codée dure de ~72 nombres premiers allant jusqu'à 7199369 qui est des balayages pour le plus petit nombre premier qui est au moins deux fois la taille actuelle, et pour les tailles plus grandes que cela calcule le premier suivant par la division d'essai de tous les nombres impairs jusqu'à la sqrt du nombre potentiel. Cette classe est immuable et ne présente aucun danger pour les fils (c'est-à-dire que les grands nombres premiers ne sont pas stockés pour d'une utilisation future).

une bonne astuce est d'utiliser un tamis partiel. Par exemple, Quel est le premier suivant le nombre N = 2534536543556?

Vérifier le module de N par rapport à une liste de petits nombres premiers. Ainsi...

mod(2534536543556,[3 5 7 11 13 17 19 23 29 31 37])
ans =
     2     1     3     6     4     1     3     4    22    16    25

nous savons que le premier suivant N doit être un nombre impair, et nous pouvons immédiatement rejeter tous les multiples impairs de cette liste de petits nombres premiers. Ces modules nous permettent de tamiser des multiples de ces petits nombres premiers. Nous avons été à l'utilisation les petits nombres premiers jusqu'à 200, nous pouvons utiliser ce schéma pour rejeter immédiatement la plupart des nombres premiers potentiels supérieurs à N, à l'exception d'une petite liste.

plus explicitement, si nous recherchons un nombre premier au-delà de 2534536543556, il ne peut pas être divisible par 2, nous n'avons donc besoin de considérer que les nombres impairs au-delà de cette valeur. Les modules ci-dessus montrent que 2534536543556 est congruente à 2 mod 3, donc 2534536543556+1 est congruente à 0 mod 3, comme doit être 2534536543556+7, 2534536543556 + 13, etc. En effet, nous pouvons passer au crible un grand nombre des chiffres sans avoir à les tester pour leur caractère primordial et sans aucune section de première instance.

de même, le fait que

mod(2534536543556,7) = 3

nous dit que 2534536543556+4 est congruent à 0 mod 7. Bien sûr, ce nombre est pair, donc nous ne pouvons l'ignorer. Mais 2534536543556+11 est un nombre impair qui est divisible par 7, comme est 2534536543556+25, etc. Encore une fois, nous pouvons exclure ces numéros clairement composite (parce qu'ils sont divisibles par 7) et donc pas premier.

en utilisant seulement la petite liste des nombres premiers jusqu'à 37, nous pouvons exclure la plupart des nombres qui suivent immédiatement notre point de départ de 2534536543556, à quelques exceptions près:

{2534536543573 , 2534536543579 , 2534536543597}

de ces nombres, sont-ils premiers?

2534536543573 = 1430239 * 1772107
2534536543579 = 99833 * 25387763

j'ai fait l'effort de fournir les principales factorisations des deux premiers nombres dans la liste. Voir qu'ils sont composites, mais les facteurs principaux sont grand. Bien sûr, cela a du sens, puisque nous avons déjà fait en sorte qu'aucun nombre qui reste ne peut avoir de petits facteurs premiers. Le troisième dans notre liste courte (2534536543597) est en fait le premier nombre premier au-delà de N. Le système de tamisage que j'ai décrit aura tendance à conduire à des nombres qui sont soit premiers, ou sont composés de facteurs premiers généralement grands. Nous avons donc fait un test explicite de primalité à seulement quelques numéros avant de trouver le prochain premier.

Un régime similaire rapidement les rendements que le prochain premier dépassant N = 1000000000000000000000000000, comme 1000000000000000000000000103.

quelques expériences avec distance inter-primes.

---

C'est un complément pour visualiser d'autres réponses.

j'ai eu les primes du 100.000 th (=1.299.709) au 200.000 th (=2.750.159)

Quelques données:

Maximum interprime distance = 148

Mean interprime distance = 15  

Interprime distance de la fréquence de l'intrigue:

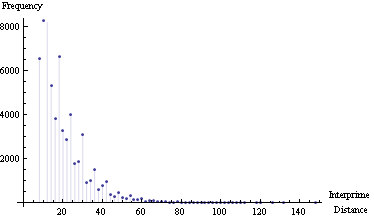
Interprime Distance par rapport au nombre premier

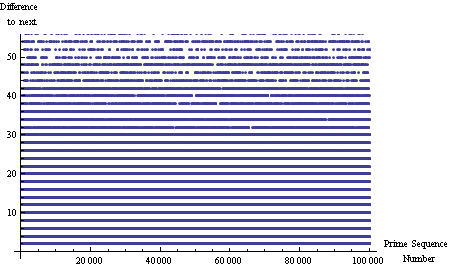
juste pour voir que c'est"aléatoire". cependant ...

il n'y a pas de fonction f(n) pour calculer le nombre premier suivant. Au lieu de cela, un nombre doit être testé pour la primalité.

il est également très utile, pour trouver le nième nombre premier, de connaître déjà tous les nombres premiers du 1er au (n-1)th, parce que ce sont les seuls nombres qui doivent être testés comme facteurs.

en raison de ces raisons, je ne serais pas surpris s'il y a un ensemble précalculé de grands nombres premiers. Il n'a pas vraiment d' expliquez-moi si certains nombres premiers ont dû être recalculés à plusieurs reprises.

Comme d'autres l'ont déjà noté, un moyen de trouver le prochain nombre premier donné l'actuel premier n'a pas encore été trouvé. Par conséquent, la plupart des algorithmes se concentrent davantage sur l'utilisation d'un moyen rapide de vérifier primalité depuis que vous devez vérifier n/2 des nombres entre votre premier connu et le prochain.

selon l'application, vous pouvez également vous en tirer avec un simple codage dur une table de recherche, comme noté par Paul Wheeler .

pour la pure nouveauté, il y a toujours cette approche:

#!/usr/bin/perl
for $p ( 2 .. 200  ) {
      next if (1x$p) =~ /^(11+)+$/;
      for ($n=1x(1+$p); $n =~ /^(11+)+$/; $n.=1) { }
      printf "next prime after %d is %d\n", $p, length($n);
}

qui produit bien sûr

next prime after 2 is 3
next prime after 3 is 5
next prime after 5 is 7
next prime after 7 is 11
next prime after 11 is 13
next prime after 13 is 17
next prime after 17 is 19
next prime after 19 is 23
next prime after 23 is 29
next prime after 29 is 31
next prime after 31 is 37
next prime after 37 is 41
next prime after 41 is 43
next prime after 43 is 47
next prime after 47 is 53
next prime after 53 is 59
next prime after 59 is 61
next prime after 61 is 67
next prime after 67 is 71
next prime after 71 is 73
next prime after 73 is 79
next prime after 79 is 83
next prime after 83 is 89
next prime after 89 is 97
next prime after 97 is 101
next prime after 101 is 103
next prime after 103 is 107
next prime after 107 is 109
next prime after 109 is 113
next prime after 113 is 127
next prime after 127 is 131
next prime after 131 is 137
next prime after 137 is 139
next prime after 139 is 149
next prime after 149 is 151
next prime after 151 is 157
next prime after 157 is 163
next prime after 163 is 167
next prime after 167 is 173
next prime after 173 is 179
next prime after 179 is 181
next prime after 181 is 191
next prime after 191 is 193
next prime after 193 is 197
next prime after 197 is 199
next prime after 199 is 211

tout le plaisir et les jeux mis à part, il est bien connu que la taille optimale de table de hachage est rigoureusement provably un nombre premier de la forme 4N−1 . Donc trouver le prochain premier est insuffisant. Vous avez à faire, les autres aussi.

autant que je me souvienne, il utilise le nombre premier à côté du double de la taille actuelle. Il ne calcule pas ce nombre premier - il table avec des nombres préchargés jusqu'à une certaine grande valeur (ne pas exactement, quelque chose environ 10.000.000). Lorsque ce nombre est atteint, il utilise un algorithme naïf pour obtenir le nombre suivant (comme curNum=curNum+1) et le valide en utilisant certaines si ces méthodes: http://en.wikipedia.org/wiki/Prime_number#Verifying_primality