Obtenir la corde la plus proche

j'ai été présenté avec ce problème il ya environ un an quand il est venu à la recherche de l'utilisateur entré des informations sur une plate-forme pétrolière dans une base de données d'informations diverses. Le but était de faire une sorte de recherche floue de chaîne de caractères qui pourrait identifier l'entrée de la base de données avec les éléments les plus communs.

une partie de la recherche a impliqué la mise en œuvre de l'algorithme distance de Levenshtein , qui détermine combien de changements doivent être apportés à une chaîne ou phrase pour la transformer en une autre chaîne ou phrase.

la mise en oeuvre que j'ai proposée était relativement simple et comportait une comparaison pondérée de la longueur des deux phrases, du nombre de changements entre chaque phrase et de la possibilité de trouver chaque mot dans l'entrée cible.

l'article est sur un site privé donc je vais faire de mon mieux pour ajouter le contenu pertinent ici:

---

Correspondance Floue est le processus d'effectuer une estimation de la similarité de deux mots ou phrases semblable à celle d'un être humain. Dans de nombreux cas, il s'agit d'identifier les mots ou les phrases qui se ressemblent le plus. Cet article décrit une solution interne au problème flou de correspondance des chaînes de caractères et son utilité pour résoudre une variété de problèmes qui peuvent nous permettre d'automatiser des tâches qui exigeaient auparavant une participation fastidieuse des utilisateurs.

Introduction

la nécessité de faire des correspondances floues des chaînes de caractères est apparue à l'origine lors de la mise au point de L'outil de validation du Golfe du Mexique. Ce qui existait était une base de données des plates-formes et des plates-formes pétrolières connues du golfe du Mexique, et les personnes achetant des assurances nous donneraient des informations Mal tapées sur leurs actifs et nous avons dû les apparier à la base de données des plates-formes connues. Lorsqu'il y avait très peu d'information fournie, le mieux que nous pouvions faire était de nous en remettre à un souscripteur pour "reconnaître" celle à laquelle il faisait référence et demandez les informations appropriées. C'est là que cette solution automatisée s'avère pratique.

j'ai passé une journée à chercher des méthodes d'appariement flou des cordes, et finalement je suis tombé sur L'algorithme de distance Levenshtein très utile sur Wikipedia.

mise en Œuvre

après avoir lu sur la théorie derrière elle, j'ai mis en œuvre et trouvé des moyens de l'optimiser. Voici à quoi ressemble mon code dans VBA:

'Calculate the Levenshtein Distance between two strings (the number of insertions,
'deletions, and substitutions needed to transform the first string into the second)
Public Function LevenshteinDistance(ByRef S1 As String, ByVal S2 As String) As Long
    Dim L1 As Long, L2 As Long, D() As Long 'Length of input strings and distance matrix
    Dim i As Long, j As Long, cost As Long 'loop counters and cost of substitution for current letter
    Dim cI As Long, cD As Long, cS As Long 'cost of next Insertion, Deletion and Substitution
    L1 = Len(S1): L2 = Len(S2)
    ReDim D(0 To L1, 0 To L2)
    For i = 0 To L1: D(i, 0) = i: Next i
    For j = 0 To L2: D(0, j) = j: Next j

    For j = 1 To L2
        For i = 1 To L1
            cost = Abs(StrComp(Mid$(S1, i, 1), Mid$(S2, j, 1), vbTextCompare))
            cI = D(i - 1, j) + 1
            cD = D(i, j - 1) + 1
            cS = D(i - 1, j - 1) + cost
            If cI <= cD Then 'Insertion or Substitution
                If cI <= cS Then D(i, j) = cI Else D(i, j) = cS
            Else 'Deletion or Substitution
                If cD <= cS Then D(i, j) = cD Else D(i, j) = cS
            End If
        Next i
    Next j
    LevenshteinDistance = D(L1, L2)
End Function

Simple, rapide, et très utile métrique. En utilisant ceci, j'ai créé deux mesures séparées pour évaluer la similarité de deux chaînes. Un que j'appelle "valuePhrase" et un que j'appelle "valueWords". valuePhrase est juste la distance Levenshtein entre les deux phrases, et valueWords divise la chaîne en mots individuels, basés sur des délimiteurs tels que des espaces, des tirets, et tout ce que vous voulez, et compare chaque mot à l'autre mot, résumant la plus courte Levenshtein distance de connexion de deux mots. Essentiellement, il évalue si les informations 'phrase' est vraiment dans un autre, tout comme un mot de permutation. J'ai passé quelques jours en tant que projet parallèle à trouver le moyen le plus efficace possible de séparer une chaîne basée sur des délimiteurs.

valueWords, valuePhrase, et la fonction de répartition:

Public Function valuePhrase#(ByRef S1$, ByRef S2$)
    valuePhrase = LevenshteinDistance(S1, S2)
End Function

Public Function valueWords#(ByRef S1$, ByRef S2$)
    Dim wordsS1$(), wordsS2$()
    wordsS1 = SplitMultiDelims(S1, " _-")
    wordsS2 = SplitMultiDelims(S2, " _-")
    Dim word1%, word2%, thisD#, wordbest#
    Dim wordsTotal#
    For word1 = LBound(wordsS1) To UBound(wordsS1)
        wordbest = Len(S2)
        For word2 = LBound(wordsS2) To UBound(wordsS2)
            thisD = LevenshteinDistance(wordsS1(word1), wordsS2(word2))
            If thisD < wordbest Then wordbest = thisD
            If thisD = 0 Then GoTo foundbest
        Next word2
foundbest:
        wordsTotal = wordsTotal + wordbest
    Next word1
    valueWords = wordsTotal
End Function

''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''
' SplitMultiDelims
' This function splits Text into an array of substrings, each substring
' delimited by any character in DelimChars. Only a single character
' may be a delimiter between two substrings, but DelimChars may
' contain any number of delimiter characters. It returns a single element
' array containing all of text if DelimChars is empty, or a 1 or greater
' element array if the Text is successfully split into substrings.
' If IgnoreConsecutiveDelimiters is true, empty array elements will not occur.
' If Limit greater than 0, the function will only split Text into 'Limit'
' array elements or less. The last element will contain the rest of Text.
''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''
Function SplitMultiDelims(ByRef Text As String, ByRef DelimChars As String, _
        Optional ByVal IgnoreConsecutiveDelimiters As Boolean = False, _
        Optional ByVal Limit As Long = -1) As String()
    Dim ElemStart As Long, N As Long, M As Long, Elements As Long
    Dim lDelims As Long, lText As Long
    Dim Arr() As String

    lText = Len(Text)
    lDelims = Len(DelimChars)
    If lDelims = 0 Or lText = 0 Or Limit = 1 Then
        ReDim Arr(0 To 0)
        Arr(0) = Text
        SplitMultiDelims = Arr
        Exit Function
    End If
    ReDim Arr(0 To IIf(Limit = -1, lText - 1, Limit))

    Elements = 0: ElemStart = 1
    For N = 1 To lText
        If InStr(DelimChars, Mid(Text, N, 1)) Then
            Arr(Elements) = Mid(Text, ElemStart, N - ElemStart)
            If IgnoreConsecutiveDelimiters Then
                If Len(Arr(Elements)) > 0 Then Elements = Elements + 1
            Else
                Elements = Elements + 1
            End If
            ElemStart = N + 1
            If Elements + 1 = Limit Then Exit For
        End If
    Next N
    'Get the last token terminated by the end of the string into the array
    If ElemStart <= lText Then Arr(Elements) = Mid(Text, ElemStart)
    'Since the end of string counts as the terminating delimiter, if the last character
    'was also a delimiter, we treat the two as consecutive, and so ignore the last elemnent
    If IgnoreConsecutiveDelimiters Then If Len(Arr(Elements)) = 0 Then Elements = Elements - 1

    ReDim Preserve Arr(0 To Elements) 'Chop off unused array elements
    SplitMultiDelims = Arr
End Function

mesures de similitude

utilisant ces deux mesures, et une troisième qui calcule simplement la distance entre deux chaînes, j'ai une série de variables que je peux exécuter un algorithme d'optimisation pour obtenir le plus grand nombre de correspondances. L'appariement flou des cordes est, en soi, une science floue, et donc en créant des mesures linéairement indépendantes pour mesurer la similarité des cordes, et ayant un ensemble connu de cordes que nous voulons faire correspondre les uns aux autres, nous pouvons trouver les paramètres qui, pour nos styles spécifiques de cordes, donnent les meilleurs résultats flous d'appariement.

au départ, l'objectif de la métrique était d'avoir une valeur de recherche faible pour une correspondance exacte, et d'augmenter les valeurs de recherche pour des mesures de plus en plus permutées. Dans un cas peu pratique, il était assez facile de le définir en utilisant un ensemble de permutations bien définies et en élaborant la formule finale de façon à obtenir des résultats de recherche plus élevés, comme on le souhaitait.

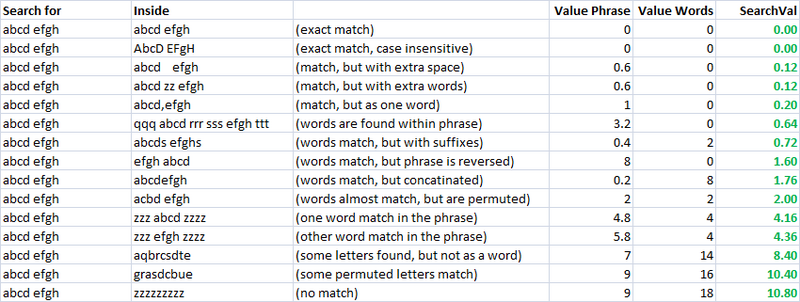
dans la capture d'écran ci-dessus, j'ai heuristique pour arriver à quelque chose que je me suis senti bien adapté à ma différence perçue entre le terme de recherche et le résultat. L'heuristique que j'ai utilisé pour Value Phrase dans le tableur ci-dessus était =valuePhrase(A2,B2)-0.8*ABS(LEN(B2)-LEN(A2)) . Je réduisais effectivement la pénalité de la distance de Levenstein de 80% de la différence de longueur des deux "phrases". De cette façon, les" phrases "qui ont la même longueur subissent la pénalité complète, mais les "phrases" qui contiennent des "informations supplémentaires" (plus longues) mais à part cela encore la plupart partagent les mêmes personnages souffrent d'une pénalité réduite. J'ai utilisé la fonction Value Words telle quelle, puis Mon heuristique finale SearchVal a été définie comme =MIN(D2,E2)*0.8+MAX(D2,E2)*0.2 - une moyenne pondérée. Quel que soit le résultat le plus faible, il est pondéré à 80% et à 20% du résultat le plus élevé. C'était juste un heuristique qui convenait à mon cas d'utilisation pour obtenir un bon taux de correspondance. Ces poids sont quelque chose que l'on pourrait alors Modifier pour obtenir le meilleur taux de correspondance avec leurs données d'essai.

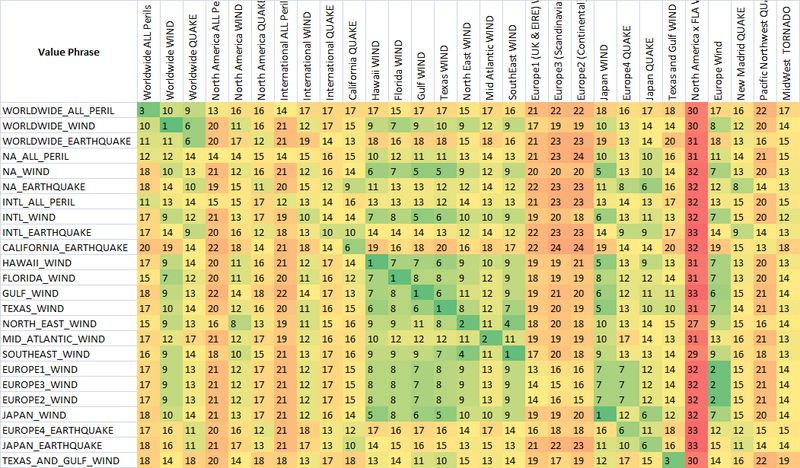
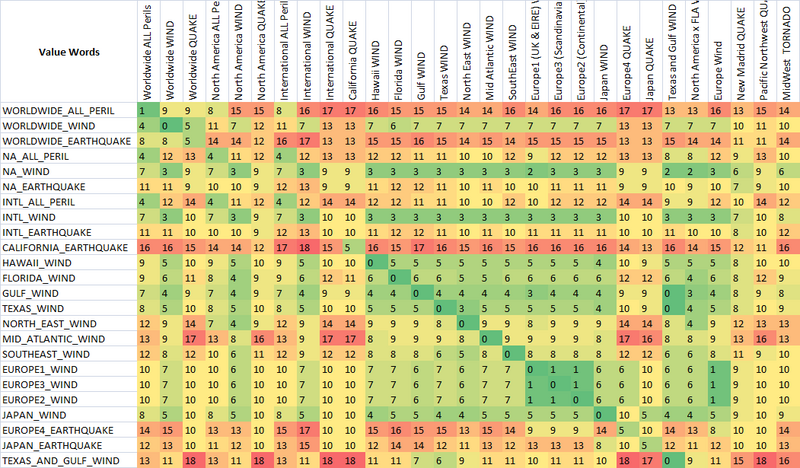
comme vous pouvez le voir, les deux dernières mesures, qui sont des mesures de chaîne flou correspondant, ont déjà une tendance naturelle à donner de faibles scores aux chaînes qui sont destinées à correspondre (en bas de la diagonale). C'est très bien.

Application Pour permettre l'optimisation de la correspondance floue, Je pondère chaque métrique. En tant que tel, chaque application de correspondance de chaîne floue peut peser les paramètres différemment. La formule qui définit le score final est une simple combinaison des mesures et de leurs poids:

value = Min(phraseWeight*phraseValue, wordsWeight*wordsValue)*minWeight
      + Max(phraseWeight*phraseValue, wordsWeight*wordsValue)*maxWeight
      + lengthWeight*lengthValue

à l'aide d'un algorithme d'optimisation (le réseau neuronal est le meilleur ici parce qu'il s'agit d'un problème discret et multidimensionnel), le but est maintenant de maximiser le nombre de correspondances. J'ai créé une fonction qui détecte le nombre de correspondances correctes de chaque jeu entre eux, comme on peut le voir dans cette capture d'écran finale. Une colonne ou une rangée obtient un point si le score le plus bas est attribué à la chaîne qui était destinée à être appariée, et des points partiels sont donnés s'il y a une égalité pour le score le plus bas, et la correspondance correcte est parmi les chaînes liées appariées. J'ai ensuite optimisé. Vous pouvez voir qu'une cellule verte est la colonne qui correspond le mieux à la rangée actuelle, et un carré bleu autour de la cellule est la rangée qui correspond le mieux à la colonne actuelle. Le score dans le coin inférieur est à peu près le nombre de matchs réussis et c'est ce que nous disons problème d'optimisation pour maximiser.

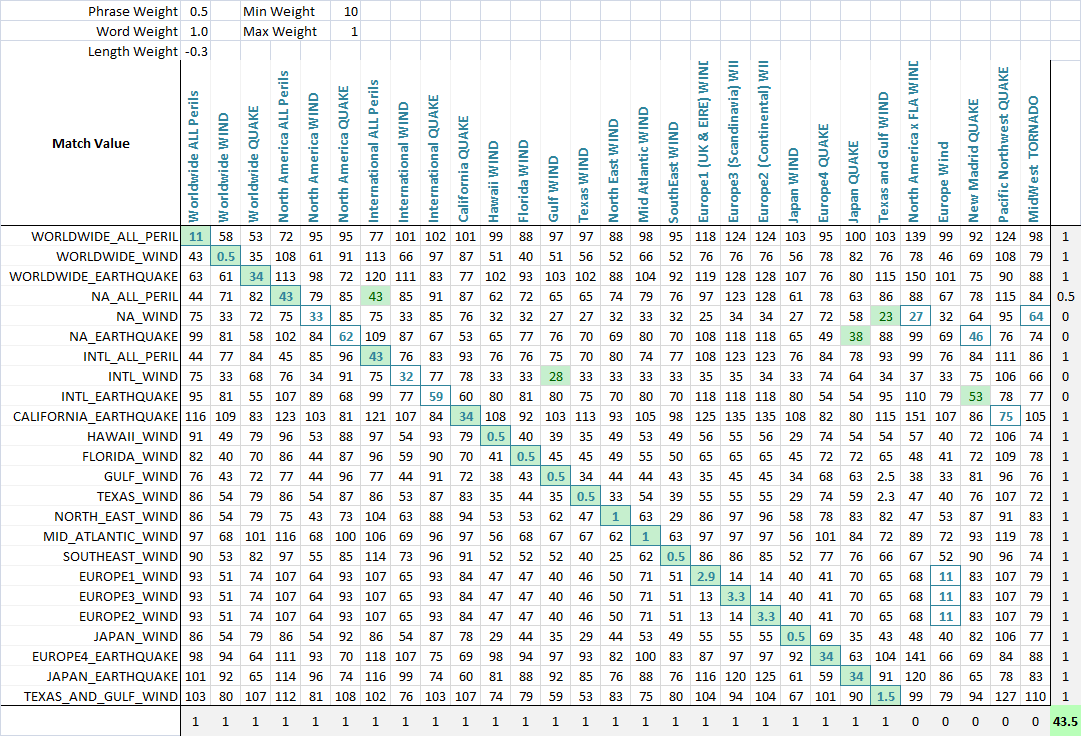
l'algorithme a été un merveilleux succès, et les paramètres de la solution en disent long sur ce type de problème. Vous remarquerez que le score optimisé était de 44, et le meilleur score possible est de 48. Les 5 colonnes à la fin sont des leurres, et n'ont pas de correspondance pour la ligne valeurs. Plus il y a de leurres, plus il sera naturellement difficile de trouver le meilleur match.

Dans ce cas particulier, la longueur des cordes est sans importance, car nous attendons des abréviations qui représentent des mots plus longs, donc le poids optimal pour la longueur est -0.3, ce qui signifie que nous ne pénalisons pas les cordes qui varient en longueur. Nous réduisons le score en prévision de ces abréviations, en donnant plus de place pour les correspondances partielles de mots pour remplacer les correspondances non-mots qui nécessitent tout simplement moins de substitutions parce que la chaîne est plus courte.

le poids du mot est 1,0 alors que le poids de la phrase est seulement 0.5, ce qui signifie que nous pénalisons les mots entiers manquants d'une chaîne et la valeur plus la phrase entière étant intacte. C'est utile parce que beaucoup de ces chaînes ont un mot en commun (le péril) où ce qui importe vraiment est de savoir si la combinaison (région et péril) est maintenue ou non.

enfin, le poids min est optimisé à 10 et le poids max à 1. Cela signifie que si le meilleur des deux scores (phrase de valeur et valeur mots) n'est pas très bon, le match est fortement pénalisé, mais nous ne pénalisons pas beaucoup le pire des deux scores. Essentiellement, cela met l'accent sur le fait d'exiger soit que la valeur soit bonne, mais pas les deux. Une sorte de mentalité de "prendre ce qu'on peut avoir".

il est vraiment fascinant ce que la valeur optimisée de ces 5 poids disent sur le genre de chaîne floue correspondance ayant lieu. Pour des cas pratiques complètement différents fuzzy correspondance de chaîne, ces paramètres sont très différents. Je l'ai utilisé pour 3 applications distinctes jusqu'à présent.

alors qu'il n'est pas utilisé dans l'optimisation finale, une feuille de benchmarking a été établie qui correspond des colonnes à eux-mêmes pour tous les résultats parfaits en bas de la diagonale, et permet à l'utilisateur de changer les paramètres pour contrôler la vitesse à laquelle les scores divergent de 0, et de noter des similitudes innées entre les phrases de recherche (qui pourrait en théorie être utilisé pour compenser les faux positifs dans le résultats)

Autres Demandes

Cette solution peut être utilisée partout où l'Utilisateur souhaite qu'un système informatique identifie une chaîne dans un ensemble de chaînes où il n'y a pas de correspondance parfaite. (Comme une correspondance approximative recherchev pour les chaînes).

---

donc, ce que vous devez prendre de ceci, est que vous probablement vous voulez utiliser une combinaison d'heuristiques de haut niveau (trouver des mots à partir d'une phrase dans l'autre phrase, longueur des deux phrases, etc) avec la mise en œuvre de L'algorithme de distance Levenshtein. Parce que décider qui est le "meilleur" match est une détermination heuristique (floue) - vous aurez à venir avec un ensemble de poids pour toutes les mesures que vous venez avec pour déterminer la similitude.

avec l'ensemble approprié d'heuristiques et de poids, vous aurez votre comparaison programme rapidement les décisions que vous avez fait.