Obtenir des erreurs standard sur les paramètres ajustés en utilisant l'optimisation.la méthode leastsq en python

mis à jour le 4/6/2016

obtenir les erreurs correctes dans les paramètres d'ajustement peut être subtil dans la plupart des cas.

pensons à ajuster une fonction y=f(x) pour laquelle vous avez un ensemble de points de données (x_i, y_i, yerr_i) , où i est un index qui s'exécute sur chacun de vos points de données.

dans la plupart des mesures physiques, l'erreur yerr_i est une incertitude systématique de l'appareil de mesure ou procédure, et il peut donc être considéré comme une constante qui ne dépend pas de i .

quelle fonction d'ajustement utiliser, et comment obtenir les erreurs de paramètre?

la méthode optimize.leastsq retournera la matrice de covariance fractionnaire. En multipliant tous les éléments de cette matrice par la variance résiduelle (c.-à-d. le chi carré réduit) et en prenant la racine carrée des éléments diagonaux vous donnera une estimation de l'écart-type de l'ajustement des paramètres. J'ai inclus le code pour le faire dans l'une des fonctions ci-dessous.

par contre, si vous utilisez optimize.curvefit , la première partie de la procédure ci-dessus (en multipliant par le chi carré réduit) est faite pour vous en coulisse. Vous devez ensuite prendre la racine carrée des éléments diagonaux de la matrice de covariance pour obtenir une estimation de l'écart-type des paramètres d'ajustement.

en outre, optimize.curvefit fournit des paramètres optionnels pour traiter des cas plus généraux, où la valeur yerr_i est différente pour chaque point de données. De la documentation :

sigma : None or M-length sequence, optional
    If not None, the uncertainties in the ydata array. These are used as
    weights in the least-squares problem
    i.e. minimising ``np.sum( ((f(xdata, *popt) - ydata) / sigma)**2 )``
    If None, the uncertainties are assumed to be 1.

absolute_sigma : bool, optional
    If False, `sigma` denotes relative weights of the data points.
    The returned covariance matrix `pcov` is based on *estimated*
    errors in the data, and is not affected by the overall
    magnitude of the values in `sigma`. Only the relative
    magnitudes of the `sigma` values matter.

Comment puis-je être sûr que mes erreurs sont correctes?

la détermination d'une estimation correcte de l'erreur-type dans les paramètres ajustés est un problème statistique complexe. Les résultats de la matrice de covariance, telle que mise en œuvre par optimize.curvefit et optimize.leastsq reposent en fait sur des hypothèses concernant la distribution de probabilité des erreurs et les interactions entre les paramètres; interactions qui peuvent exister, en fonction de votre fonction d'ajustement spécifique f(x) .

à mon avis, la meilleure façon de traiter un f(x) compliqué est d'utiliser la méthode bootstrap, qui est décrite dans ce lien .

voyons quelques exemples

Tout d'abord, un code boilerplate. Définissons une fonction de ligne et générons des données avec des erreurs aléatoires. Nous allons générer un jeu de données avec une petite erreur aléatoire.

import numpy as np
from scipy import optimize
import random

def f( x, p0, p1, p2):
    return p0*x + 0.4*np.sin(p1*x) + p2

def ff(x, p):
    return f(x, *p)

# These are the true parameters
p0 = 1.0
p1 = 40
p2 = 2.0

# These are initial guesses for fits:
pstart = [
    p0 + random.random(),
    p1 + 5.*random.random(), 
    p2 + random.random()
]

%matplotlib inline
import matplotlib.pyplot as plt
xvals = np.linspace(0., 1, 120)
yvals = f(xvals, p0, p1, p2)

# Generate data with a bit of randomness
# (the noise-less function that underlies the data is shown as a blue line)

xdata = np.array(xvals)
np.random.seed(42)
err_stdev = 0.2
yvals_err =  np.random.normal(0., err_stdev, len(xdata))
ydata = f(xdata, p0, p1, p2) + yvals_err

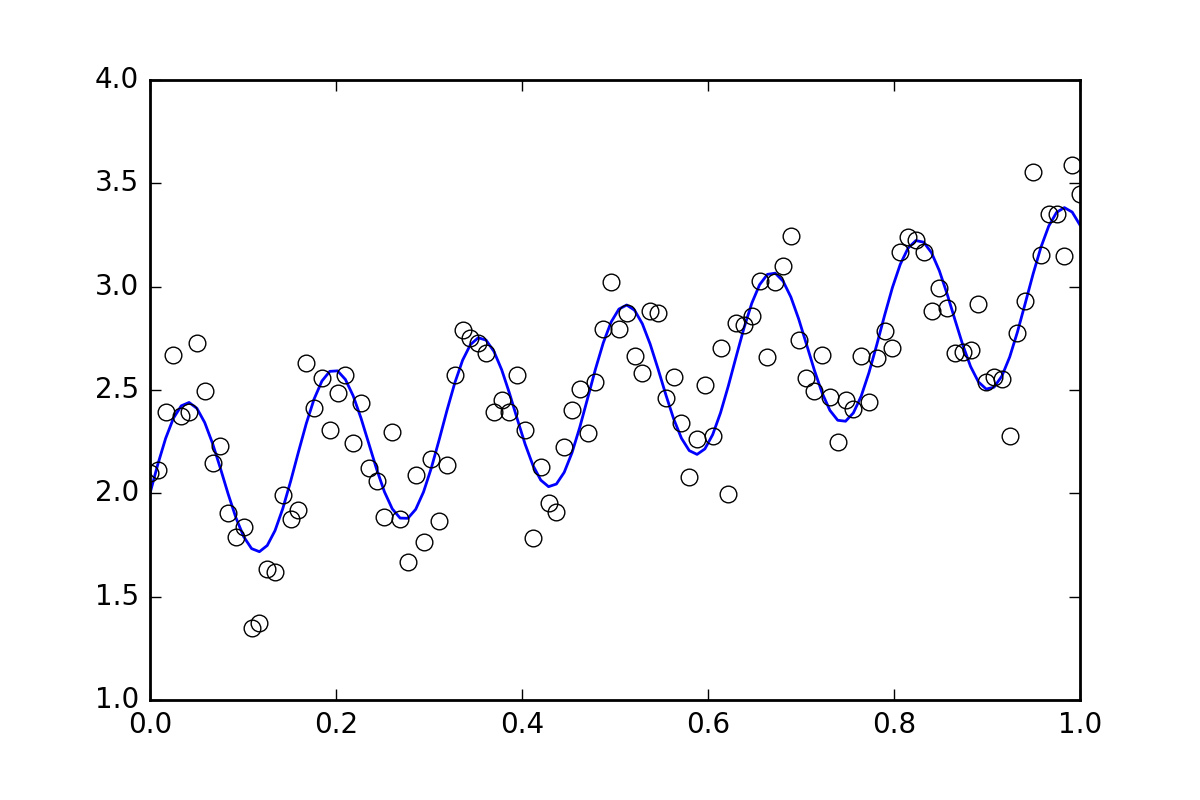
plt.plot(xvals, yvals)
plt.plot(xdata, ydata, 'o', mfc='None')

maintenant, adaptons la fonction en utilisant les différentes méthodes disponibles:

`optimiser.leastsq '

def fit_leastsq(p0, datax, datay, function):

    errfunc = lambda p, x, y: function(x,p) - y

    pfit, pcov, infodict, errmsg, success = \
        optimize.leastsq(errfunc, p0, args=(datax, datay), \
                          full_output=1, epsfcn=0.0001)

    if (len(datay) > len(p0)) and pcov is not None:
        s_sq = (errfunc(pfit, datax, datay)**2).sum()/(len(datay)-len(p0))
        pcov = pcov * s_sq
    else:
        pcov = np.inf

    error = [] 
    for i in range(len(pfit)):
        try:
          error.append(np.absolute(pcov[i][i])**0.5)
        except:
          error.append( 0.00 )
    pfit_leastsq = pfit
    perr_leastsq = np.array(error) 
    return pfit_leastsq, perr_leastsq 

pfit, perr = fit_leastsq(pstart, xdata, ydata, ff)

print("\n# Fit parameters and parameter errors from lestsq method :")
print("pfit = ", pfit)
print("perr = ", perr)

# Fit parameters and parameter errors from lestsq method :
pfit =  [  1.04951642  39.98832634   1.95947613]
perr =  [ 0.0584024   0.10597135  0.03376631]

`optimiser.curve_fit`

def fit_curvefit(p0, datax, datay, function, yerr=err_stdev, **kwargs):
    """
    Note: As per the current documentation (Scipy V1.1.0), sigma (yerr) must be:
        None or M-length sequence or MxM array, optional
    Therefore, replace:
        err_stdev = 0.2
    With:
        err_stdev = [0.2 for item in xdata]
    Or similar, to create an M-length sequence for this example.
    """
    pfit, pcov = \
         optimize.curve_fit(f,datax,datay,p0=p0,\
                            sigma=yerr, epsfcn=0.0001, **kwargs)
    error = [] 
    for i in range(len(pfit)):
        try:
          error.append(np.absolute(pcov[i][i])**0.5)
        except:
          error.append( 0.00 )
    pfit_curvefit = pfit
    perr_curvefit = np.array(error)
    return pfit_curvefit, perr_curvefit 

pfit, perr = fit_curvefit(pstart, xdata, ydata, ff)

print("\n# Fit parameters and parameter errors from curve_fit method :")
print("pfit = ", pfit)
print("perr = ", perr)

# Fit parameters and parameter errors from curve_fit method :
pfit =  [  1.04951642  39.98832634   1.95947613]
perr =  [ 0.0584024   0.10597135  0.03376631]

'bootstrap`

def fit_bootstrap(p0, datax, datay, function, yerr_systematic=0.0):

    errfunc = lambda p, x, y: function(x,p) - y

    # Fit first time
    pfit, perr = optimize.leastsq(errfunc, p0, args=(datax, datay), full_output=0)


    # Get the stdev of the residuals
    residuals = errfunc(pfit, datax, datay)
    sigma_res = np.std(residuals)

    sigma_err_total = np.sqrt(sigma_res**2 + yerr_systematic**2)

    # 100 random data sets are generated and fitted
    ps = []
    for i in range(100):

        randomDelta = np.random.normal(0., sigma_err_total, len(datay))
        randomdataY = datay + randomDelta

        randomfit, randomcov = \
            optimize.leastsq(errfunc, p0, args=(datax, randomdataY),\
                             full_output=0)

        ps.append(randomfit) 

    ps = np.array(ps)
    mean_pfit = np.mean(ps,0)

    # You can choose the confidence interval that you want for your
    # parameter estimates: 
    Nsigma = 1. # 1sigma gets approximately the same as methods above
                # 1sigma corresponds to 68.3% confidence interval
                # 2sigma corresponds to 95.44% confidence interval
    err_pfit = Nsigma * np.std(ps,0) 

    pfit_bootstrap = mean_pfit
    perr_bootstrap = err_pfit
    return pfit_bootstrap, perr_bootstrap 

pfit, perr = fit_bootstrap(pstart, xdata, ydata, ff)

print("\n# Fit parameters and parameter errors from bootstrap method :")
print("pfit = ", pfit)
print("perr = ", perr)

# Fit parameters and parameter errors from bootstrap method :
pfit =  [  1.05058465  39.96530055   1.96074046]
perr =  [ 0.06462981  0.1118803   0.03544364]

Observations

nous commençons déjà à voir quelque chose d'intéressant, les paramètres et les estimations d'erreur pour les trois méthodes presque d'accord. Ce qui est bon!

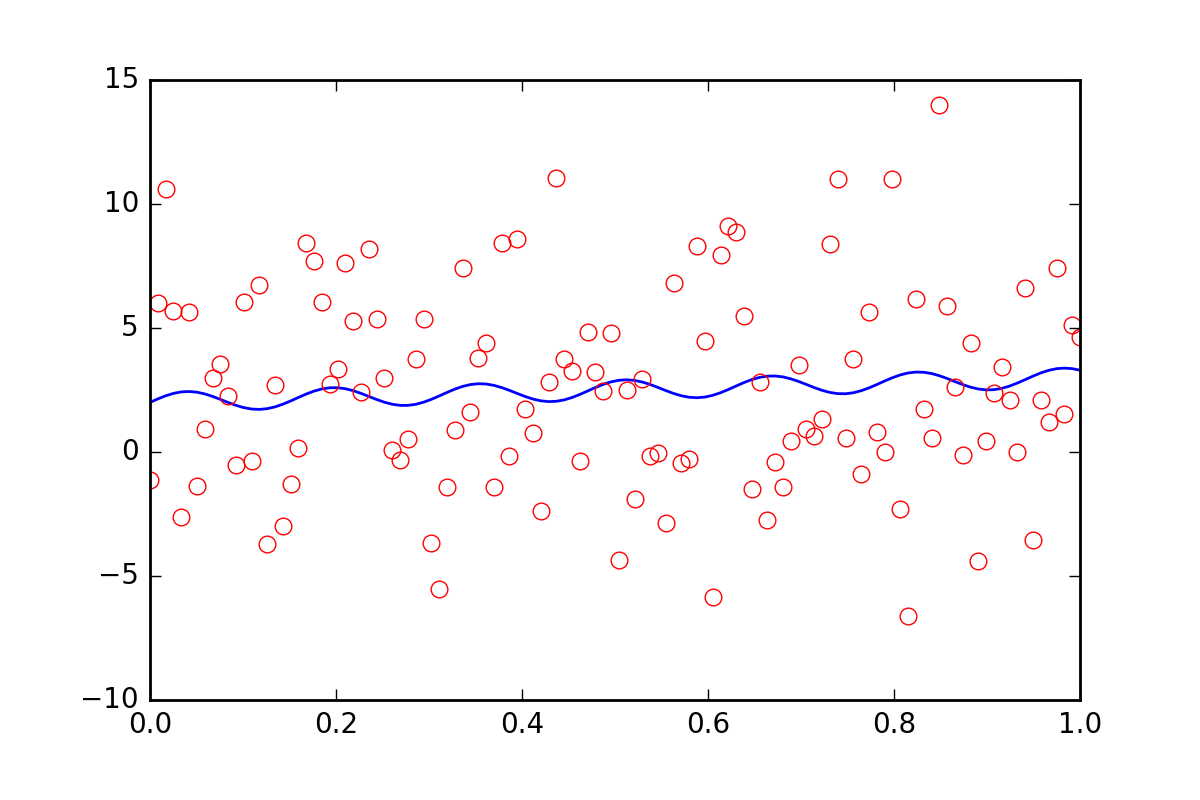
maintenant, supposons que nous voulions dire aux fonctions appropriées qu'il y a une autre incertitude dans nos données, peut-être une incertitude systématique qui contribuerait à une erreur supplémentaire de vingt fois la valeur de err_stdev . C'est beaucoup de l'erreur, en fait, si nous simulons certains données avec ce genre d'erreur, il ressemblerait à ceci:

Il n'y a certainement aucun espoir que nous pourrions récupérer les paramètres d'ajustement avec ce niveau de bruit.

pour commencer, réalisons que leastsq ne nous permet même pas d'entrer cette nouvelle information d'erreur systématique. Voyons ce que fait curve_fit quand on lui parle de l'erreur:

pfit, perr = fit_curvefit(pstart, xdata, ydata, ff, yerr=20*err_stdev)

print("\nFit parameters and parameter errors from curve_fit method (20x error) :")
print("pfit = ", pfit)
print("perr = ", perr)

Fit parameters and parameter errors from curve_fit method (20x error) :
pfit =  [  1.04951642  39.98832633   1.95947613]
perr =  [ 0.0584024   0.10597135  0.03376631]

quoi?? Cela doit certainement être mauvais!

c'était la fin de l'histoire, mais récemment curve_fit a ajouté le absolute_sigma paramètre optionnel:

pfit, perr = fit_curvefit(pstart, xdata, ydata, ff, yerr=20*err_stdev, absolute_sigma=True)

print("\n# Fit parameters and parameter errors from curve_fit method (20x error, absolute_sigma) :")
print("pfit = ", pfit)
print("perr = ", perr)

# Fit parameters and parameter errors from curve_fit method (20x error, absolute_sigma) :
pfit =  [  1.04951642  39.98832633   1.95947613]
perr =  [ 1.25570187  2.27847504  0.72600466]

c'est un peu mieux, mais encore un peu louche. curve_fit pense que nous pouvons obtenir un ajustement de ce signal bruyant, avec un niveau de 10% d'erreur dans le p1 paramètre. Voyons ce que bootstrap a à dire:

pfit, perr = fit_bootstrap(pstart, xdata, ydata, ff, yerr_systematic=20.0)

print("\nFit parameters and parameter errors from bootstrap method (20x error):")
print("pfit = ", pfit)
print("perr = ", perr)

Fit parameters and parameter errors from bootstrap method (20x error):
pfit =  [  2.54029171e-02   3.84313695e+01   2.55729825e+00]
perr =  [  6.41602813  13.22283345   3.6629705 ]

Ah, c'est peut-être une meilleure estimation de l'erreur dans notre ajustement de paramètre. bootstrap pense savoir p1 avec environ 34% d'incertitude.

résumé

optimize.leastsq et optimize.curvefit nous fournit un moyen d'estimer les erreurs dans les paramètres ajustés, mais nous ne pouvons pas simplement utiliser ces méthodes sans les questionner un peu. Le bootstrap est une méthode statistique qui utilise la force brute, et à mon avis, il a tendance à mieux travailler dans des situations qui peuvent être plus difficiles à interpréter.

je recommande fortement d'examiner un problème particulier, et d'essayer curvefit et bootstrap . Si elles sont similaires, alors curvefit est beaucoup moins cher à calculer, donc probablement utile d'utiliser. S'ils diffèrent de manière significative, alors mon argent serait sur le bootstrap .

trouvé votre question tout en essayant de répondre à mon propre similaire question . Réponse courte. Le cov_x que les extrants de leastsq devraient être multipliés par la variance résiduelle. c'est à dire

s_sq = (func(popt, args)**2).sum()/(len(ydata)-len(p0))
pcov = pcov * s_sq

comme dans curve_fit.py . C'est parce que leastsq produit la matrice de covariance fractionnaire. Mon gros problème était que la variance résiduelle apparaît comme quelque chose d'autre lors de googler.

variance résiduelle est simplement réduite chi carré de votre ajustement.

il est possible de calculer exactement les erreurs dans le cas d'une régression linéaire. Et en effet la fonction leastsq donne des valeurs différentes:

import numpy as np
from scipy.optimize import leastsq
import matplotlib.pyplot as plt

A = 1.353
B = 2.145

yerr = 0.25

xs = np.linspace( 2, 8, 1448 )
ys = A * xs + B + np.random.normal( 0, yerr, len( xs ) )

def linearRegression( _xs, _ys ):
    if _xs.shape[0] != _ys.shape[0]:
        raise ValueError( 'xs and ys must be of the same length' )
    xSum = ySum = xxSum = yySum = xySum = 0.0
    numPts = 0

    for i in range( len( _xs ) ):
        xSum += _xs[i]
        ySum += _ys[i]
        xxSum += _xs[i] * _xs[i]
        yySum += _ys[i] * _ys[i]
        xySum += _xs[i] * _ys[i]
        numPts += 1

    k = ( xySum - xSum * ySum / numPts ) / ( xxSum - xSum * xSum / numPts )
    b = ( ySum - k * xSum ) / numPts
    sk = np.sqrt( ( ( yySum - ySum * ySum / numPts ) / ( xxSum - xSum * xSum / numPts ) - k**2 ) / numPts )
    sb = np.sqrt( ( yySum - ySum * ySum / numPts ) - k**2 * ( xxSum - xSum * xSum / numPts ) ) / numPts

    return [ k, b, sk, sb ]

def linearRegressionSP( _xs, _ys ):
    defPars = [ 0, 0 ]
    pars, pcov, infodict, errmsg, success = \
    leastsq( lambda _pars, x, y: y - ( _pars[0] * x + _pars[1] ), defPars, args = ( _xs, _ys ), full_output=1 )

    errs = []
    if pcov is not None:
        if( len( _xs ) > len(defPars) ) and pcov is not None:
            s_sq = ( ( ys - ( pars[0] * _xs + pars[1] ) )**2 ).sum() / ( len( _xs ) - len( defPars ) )
            pcov *= s_sq

        for j in range( len( pcov ) ):
            errs.append( pcov[j][j]**0.5 )
    else:
        errs = [ np.inf, np.inf ]
    return np.append( pars, np.array( errs ) )

regr1 = linearRegression( xs, ys )
regr2 = linearRegressionSP( xs, ys )

print( regr1 )
print( 'Calculated sigma = %f' %  ( regr1[3] * np.sqrt( xs.shape[0] ) ) )
print( regr2 )
#print( 'B = %f must be in ( %f,\t%f )' % ( B, regr1[1] - regr1[3], regr1[1] + regr1[3] ) )


plt.plot( xs, ys, 'bo' )
plt.plot( xs, regr1[0] * xs + regr1[1] )
plt.show()

sortie:

[1.3481681543925064, 2.1729338701374137, 0.0036028493647274687, 0.0062446292528624348]
Calculated sigma = 0.237624 # quite close to yerr
[ 1.34816815  2.17293387  0.00360534  0.01907908]

c'est intéressant quels résultats curvefit et bootstrap donneront...