Geo Escrime - point à l'intérieur/à l'extérieur du polygone

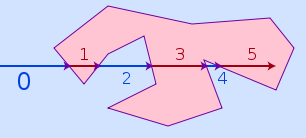
si je me souviens bien, l'algorithme est de tracer une ligne horizontale à travers votre point de test. Comptez le nombre de lignes du polygone que vous croisez pour atteindre votre point.

si la réponse est étrange, vous êtes à l'intérieur. Si la réponse est égale, vous êtes dehors.

Edit: Ouais, ce il , a dit ( Wikipedia ):

code C#

bool IsPointInPolygon(List<Loc> poly, Loc point)
{
    int i, j;
    bool c = false;
    for (i = 0, j = poly.Count - 1; i < poly.Count; j = i++)
    {
        if ((((poly[i].Lt <= point.Lt) && (point.Lt < poly[j].Lt)) 
                || ((poly[j].Lt <= point.Lt) && (point.Lt < poly[i].Lt))) 
                && (point.Lg < (poly[j].Lg - poly[i].Lg) * (point.Lt - poly[i].Lt) 
                    / (poly[j].Lt - poly[i].Lt) + poly[i].Lg))

            c = !c;
        }
    }

    return c;
}

Classe Loc

public class Loc
{
    private double lt;
    private double lg;

    public double Lg
    {
        get { return lg; }
        set { lg = value; }
    }

    public double Lt
    {
        get { return lt; }
        set { lt = value; }
    }

    public Loc(double lt, double lg)
    {
        this.lt = lt;
        this.lg = lg;
    }
}

après avoir cherché sur le web et essayé diverses implémentations et les avoir portées de C++ à c# j'ai finalement eu mon code correctement:

        public static bool PointInPolygon(LatLong p, List<LatLong> poly)
    {
        int n = poly.Count();

        poly.Add(new LatLong { Lat = poly[0].Lat, Lon = poly[0].Lon });
        LatLong[] v = poly.ToArray();

        int wn = 0;    // the winding number counter

        // loop through all edges of the polygon
        for (int i = 0; i < n; i++)
        {   // edge from V[i] to V[i+1]
            if (v[i].Lat <= p.Lat)
            {         // start y <= P.y
                if (v[i + 1].Lat > p.Lat)      // an upward crossing
                    if (isLeft(v[i], v[i + 1], p) > 0)  // P left of edge
                        ++wn;            // have a valid up intersect
            }
            else
            {                       // start y > P.y (no test needed)
                if (v[i + 1].Lat <= p.Lat)     // a downward crossing
                    if (isLeft(v[i], v[i + 1], p) < 0)  // P right of edge
                        --wn;            // have a valid down intersect
            }
        }
        if (wn != 0)
            return true;
        else
            return false;

    }

    private static int isLeft(LatLong P0, LatLong P1, LatLong P2)
    {
        double calc = ((P1.Lon - P0.Lon) * (P2.Lat - P0.Lat)
                - (P2.Lon - P0.Lon) * (P1.Lat - P0.Lat));
        if (calc > 0)
            return 1;
        else if (calc < 0)
            return -1;
        else
            return 0;
    }

la fonction isLeft me donnait des problèmes d'arrondi et j'ai passé des heures sans réaliser que je faisais la conversion mal, alors pardonnez-moi pour le blocage boiteux si à la fin de cette fonction.

BTW, c'est le code et l'article d'origine: http://softsurfer.com/Archive/algorithm_0103/algorithm_0103.htm

je pense qu'il y a une solution plus simple et plus efficace.

voici le code en C++. Je devrais être simple pour le convertir en C#.

int pnpoly(int npol, float *xp, float *yp, float x, float y)
{
  int i, j, c = 0;
  for (i = 0, j = npol-1; i < npol; j = i++) {
    if ((((yp[i] <= y) && (y < yp[j])) ||
         ((yp[j] <= y) && (y < yp[i]))) &&
        (x < (xp[j] - xp[i]) * (y - yp[i]) / (yp[j] - yp[i]) + xp[i]))
      c = !c;
  }
  return c;
}

de loin la meilleure explication et la mise en œuvre peut être trouvée à Point Dans Le Polygone Numéro Du Bobinage De L'Inclusion

il y a même une implémentation C++ à la fin de l'article bien expliqué. Ce site contient également de grands algorithmes/solutions pour d'autres problèmes basés sur la géométrie.

j'ai modifié et utilisé L'implémentation C++ et j'ai aussi créé une implémentation C#. Vous voulez certainement utiliser L'enroulement Algorithme de nombre car il est plus précis que l'algorithme de franchissement de bord et il est très rapide.

juste une mise en garde (en utilisant answer car je ne peux pas commenter), si vous voulez utiliser point-in-polygon pour géo clôture, alors vous devez changer votre algorithme pour travailler avec des coordonnées sphériques. La longitude -180 est la même que la longitude 180 et point-in-polygon cassera dans une telle situation.

la solution complète dans asp.Net C#, vous pouvez voir le détail complet ici,vous pouvez voir comment trouver point(lat, lon) si son intérieur ou à l'extérieur du polygone en utilisant la latitude et la longitude ? Lien De Référence De L'Article

private static bool checkPointExistsInGeofencePolygon (string latlnglist, string lat, string lng) {

    List<Loc> objList = new List<Loc>();
    // sample string should be like this strlatlng = "39.11495,-76.873259|39.114588,-76.872808|39.112921,-76.870373|";
    string[] arr = latlnglist.Split('|');
    for (int i = 0; i <= arr.Length - 1; i++)
    {
        string latlng = arr[i];
        string[] arrlatlng = latlng.Split(',');

        Loc er = new Loc(Convert.ToDouble(arrlatlng[0]), Convert.ToDouble(arrlatlng[1]));
        objList.Add(er);
    }
    Loc pt = new Loc(Convert.ToDouble(lat), Convert.ToDouble(lng));

    if (IsPointInPolygon(objList, pt) == true)
    {
          return true;
    }
    else
    {
           return false;
    }
}
private static bool IsPointInPolygon(List<Loc> poly, Loc point)
{
    int i, j;
    bool c = false;
    for (i = 0, j = poly.Count - 1; i < poly.Count; j = i++)
    {
        if ((((poly[i].Lt <= point.Lt) && (point.Lt < poly[j].Lt)) |
            ((poly[j].Lt <= point.Lt) && (point.Lt < poly[i].Lt))) &&
            (point.Lg < (poly[j].Lg - poly[i].Lg) * (point.Lt - poly[i].Lt) / (poly[j].Lt - poly[i].Lt) + poly[i].Lg))
            c = !c;
    }
    return c;
}

vérifier si un point est à l'intérieur d'un polygone ou non -

considérons le polygone qui a des sommets a1,a2,a3,a4,a5. Les étapes suivantes devraient aider à déterminer si le point P se trouve à l'intérieur ou à l'extérieur du polygone.

calculer la surface vectorielle du triangle formé par le bord a1->a2 et les vecteurs reliant a2 à P et P à a1. De même, calculer la zone vectorielle de chacun des triangles possibles ayant un côté comme le côté de la polygone et les deux autres reliant P à ce côté.

Pour un point à l'intérieur d'un polygone, chacun des triangles doivent avoir des zone. Même si l'un des triangles est négative, le point P se distingue du polygone.

pour calculer la surface d'un triangle donné vecteurs représentant ses 3 arêtes, se référer à http://www.jtaylor1142001.net/calcjat/Solutions/VCrossProduct/VCPATriangle.htm

Le problème est plus facile si votre polygone est convexe. Si oui, vous pouvez faire un test simple pour chaque ligne pour voir si le point est à l'intérieur ou à l'extérieur de cette ligne (qui s'étendent à l'infini dans les deux directions). Sinon, pour les polygones concaves, dessinez un rayon imaginaire de votre point à l'infini (dans n'importe quelle direction). Compter combien de fois il franchit une ligne de démarcation. Bizarre à dire le point est à l'intérieur, même signifie que le point est à l'extérieur.

ce dernier algorithme est plus compliqué qu'il n'y paraît. Vous devrez être très prudent sur ce qui se passe quand votre rayon imaginaire frappe exactement l'un des sommets du polygone.

si votre rayon imaginaire va dans la direction-x, vous pouvez choisir seulement de compter les lignes qui incluent au moins un point dont la coordonnée y est strictement inférieure à la coordonnée y de votre point. C'est comme ça que vous obtenez la plupart des cas de bord bizarre à travailler correctement.

si vous avez un simple polygone (aucune des lignes ne se croisent) et que vous n'avez pas de trous, vous pouvez aussi trianguler le polygone, ce que vous allez probablement faire de toute façon dans une application GIS pour dessiner une boîte, puis tester pour les points dans chaque triangle. Si vous avez un petit nombre d'arêtes du polygone, mais un grand nombre de points c'est rapide.

Pour un point intéressant dans le triangle voir texte du lien

autrement utiliser definately le règle d'enroulement plutôt que traversée de bord, traversée de bord a de réels problèmes avec les points sur les bords, qui si vos données sont générées sous forme D'un GPS avec une précision limitée est très probable.

le polygone est défini comme une liste séquentielle de paires de points A, B, C.... A. pas de côté A-B, B-C... croise tout autre côté

déterminer la case Xmin, Xmax, Ymin, Ymax

case 1 le point d'essai P se trouve à l'extérieur de la case

case 2 le point D'essai P se trouve à l'intérieur de la case:

déterminer le "diamètre" D de la boîte {[Xmin, Ymin] - [Xmax, Ymax]} (et Ajouter un petit extra pour éviter toute confusion possible avec D étant sur un côté)

déterminer les gradients M de tous les côtés

trouver un gradient Mt le plus différent de tous les gradients M

la ligne d'essai court de P à la pente Mt a distance D.

mettre le nombre d'intersections à zéro

pour chacun des côtés A-B, B-C essai pour l'intersection de P-D avec un côté à partir de son début jusqu'à sa fin. Incrémenter le compteur de intersection si nécessaire. Note qu'un zéro la distance de P à l'intersection indique que P est SUR un côté

un nombre impair indique que P est à l'intérieur du polygone

j'ai traduit la méthode c# en Php et j'ai ajouté de nombreux commentaires pour comprendre le code.



Description des polygones:

Vérifier si un point est à l'intérieur ou à l'extérieur d'un polygone. Cette procédure utilise les coordonnées gps et cela fonctionne quand polygon a une petite zone géographique.





ENTRÉE:

$poly: tableau de Point: polygone de sommets liste; [{Point}, {Point}, ...];

$point: point à vérifier; Point: {"lat" = > " X. xxx", "lng" = > " Y. yyy"}





Quand $c est false, le nombre d'intersections avec le polygone est pair, donc le point est à l'extérieur du polygone;

quand $c est vrai, le nombre d'intersections avec le polygone est impair, donc le point est à l'intérieur du polygone;

$n est le nombre de sommets dans le polygone;

pour chaque vertex en polygone, la méthode calcule la ligne à travers le vertex courant et le vertex précédent et vérifie si les deux lignes ont un point d'intersection.

$c change when intersection point exists.

Ainsi, la méthode peut retourner true si le point est à l'intérieur du polygone, sinon retourner false.

class PolygonHelps {

    public static function isPointInPolygon(&$poly, $point){

        $c = false; 
        $n = $j = count($poly);


        for ($i = 0, $j = $n - 1; $i < $n; $j = $i++){

            if ( ( ( ( $poly[$i]->lat <= $point->lat ) && ( $point->lat < $poly[$j]->lat ) ) 
                || ( ( $poly[$j]->lat <= $point->lat ) && ( $point->lat < $poly[$i]->lat ) ) ) 

            && ( $point->lng <   ( $poly[$j]->lng - $poly[$i]->lng ) 
                               * ( $point->lat    - $poly[$i]->lat ) 
                               / ( $poly[$j]->lat - $poly[$i]->lat ) 
                               +   $poly[$i]->lng ) ){

                $c = !$c;
            }
        }

        return $c;
    }
}

j'ajoute un détail pour aider les gens qui vivent dans le... sud de terre!! Si vous êtes au Brésil (c'est mon cas), notre accord GPS sont tous négatifs. Et tous ces algo donnent de mauvais résultats.

la façon la plus facile si d'utiliser les valeurs absolues de la Lat et Long de tout point. Et dans ce cas, l'algo de Jan Kobersky est parfait.