Production de coordonnées triangulaires/hexagonales (xyz)
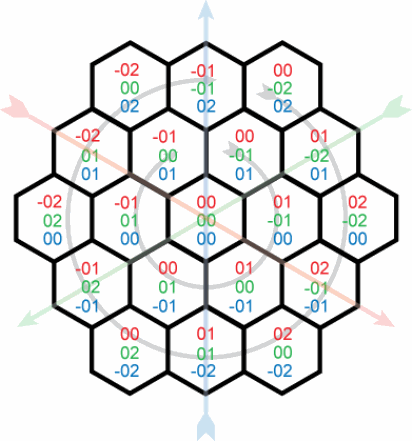
j'essaie de trouver une fonction itérative qui génère des coordonnées xyz pour une grille hexagonale. Avec une position d'hexagone de départ (disons 0,0 pour la simplicité), je veux calculer les coordonnées pour chaque "anneau" successif d'hexagones, comme illustré ici:
jusqu'à présent, tout ce que j'ai réussi à trouver est ceci (exemple en javascript):
var radius = 3
var xyz = [0,0,0];
// for each ring
for (var i = 0; i < radius; i++) {
var tpRing = i*6;
var tpVect = tpRing/3;
// for each vector of ring
for (var j = 0; j < 3; j++) {
// for each tile in vector
for(var k = 0; k < tpVect; k++) {
xyz[0] = ???;
xyz[1] = ???;
xyz[2] = ???;
console.log(xyz);
}
}
}
je sais que chaque anneau contient six points de plus que le précédent et chaque vecteur de 120° contient un point supplémentaire pour chaque pas à partir du centre. Je sais aussi que x + y + z = 0 pour tous les carreaux. Mais comment puis-je générer une liste de coordonnées qui suivent la séquence ci-dessous?
0, 0, 0
0,-1, 1
1,-1, 0
1, 0,-1
0, 1,-1
-1, 1, 0
-1, 0, 1
0,-2, 2
1,-2, 1
2,-2, 0
2,-1,-1
2, 0,-2
1, 1,-2
0, 2,-2
-1, 2,-1
-2, 2, 0
-2, 1, 1
-2, 0, 2
-1,-1, 2
4 réponses
une autre solution possible, qui fonctionne dans o (rayon 2 ), contrairement au o (rayon 4 ) de la solution de tehMick (aux frais de beaucoup de style) est ceci:
radius = 4
for r in range(radius):
print "radius %d" % r
x = 0
y = -r
z = +r
print x,y,z
for i in range(r):
x = x+1
z = z-1
print x,y,z
for i in range(r):
y = y+1
z = z-1
print x,y,z
for i in range(r):
x = x-1
y = y+1
print x,y,z
for i in range(r):
x = x-1
z = z+1
print x,y,z
for i in range(r):
y = y-1
z = z+1
print x,y,z
for i in range(r-1):
x = x+1
y = y-1
print x,y,z
ou écrit un peu plus concise:
radius = 4
deltas = [[1,0,-1],[0,1,-1],[-1,1,0],[-1,0,1],[0,-1,1],[1,-1,0]]
for r in range(radius):
print "radius %d" % r
x = 0
y = -r
z = +r
print x,y,z
for j in range(6):
if j==5:
num_of_hexas_in_edge = r-1
else:
num_of_hexas_in_edge = r
for i in range(num_of_hexas_in_edge):
x = x+deltas[j][0]
y = y+deltas[j][1]
z = z+deltas[j][2]
print x,y,z
c'est inspiré par le fait que les hexagones sont en fait à l'extérieur d'un hexagone ils sont eux-mêmes, de sorte que vous pouvez trouver les coordonnées de 1 de ses points, et puis calculer les autres en se déplaçant sur ses 6 bords.
N'est pas seulement x + y + z = 0 , mais les valeurs absolues de x, y et z sont égales à deux fois le rayon de l'anneau. Cela devrait être suffisant pour identifier chaque hexagone sur chaque anneau:
var radius = 4;
for(var i = 0; i < radius; i++)
{
for(var j = -i; j <= i; j++)
for(var k = -i; k <= i; k++)
for(var l = -i; l <= i; l++)
if(Math.abs(j) + Math.abs(k) + Math.abs(l) == i*2 && j + k + l == 0)
console.log(j + "," + k + "," + l);
console.log("");
}c'était un puzzle amusant.
o(rayon 2 ) mais avec (espérons) un peu plus de style que la solution de Ofri. il m'est apparu que les coordonnées pouvaient être générées comme si vous" marchiez " autour de l'anneau en utilisant un vecteur de direction (déplacement), et qu'un virage était équivalent à déplacer le zéro autour du vecteur de déplacement.
cette version a aussi l'avantage sur la solution D'Eric en ce qu'elle ne touche jamais les coordonnées invalides (Eric les rejette, mais celui-ci n'a même pas à les tester).
# enumerate coords in rings 1..n-1; this doesn't work for the origin
for ring in range(1,4):
# start in the upper right corner ...
(x,y,z) = (0,-ring,ring)
# ... moving clockwise (south-east, or +x,-z)
move = [1,0,-1]
# each ring has six more coordinates than the last
for i in range(6*ring):
# print first to get the starting hex for this ring
print "%d/%d: (%d,%d,%d) " % (ring,i,x,y,z)
# then move to the next hex
(x,y,z) = map(sum, zip((x,y,z), move))
# when a coordinate has a zero in it, we're in a corner of
# the ring, so we need to turn right
if 0 in (x,y,z):
# left shift the zero through the move vector for a
# right turn
i = move.index(0)
(move[i-1],move[i]) = (move[i],move[i-1])
print # blank line between rings
trois hourras pour la séquence de découpage de python.
Ok, après avoir essayé les deux options, j'ai choisi la solution D'Ofri car elle est un tout petit peu plus rapide et m'a permis de fournir facilement une valeur initiale d'offset. Mon code ressemble maintenant à ceci:
var xyz = [-2,2,0];
var radius = 16;
var deltas = [[1,0,-1],[0,1,-1],[-1,1,0],[-1,0,1],[0,-1,1],[1,-1,0]];
for(var i = 0; i < radius; i++) {
var x = xyz[0];
var y = xyz[1]-i;
var z = xyz[2]+i;
for(var j = 0; j < 6; j++) {
for(var k = 0; k < i; k++) {
x = x+deltas[j][0]
y = y+deltas[j][1]
z = z+deltas[j][2]
placeTile([x,y,z]);
}
}
}
la méthode "placetille" utilise cloneNode pour copier un élément svg prédéfini et il faut environ 0.5 ms par tuile pour exécuter ce qui est plus que suffisant. Un grand merci à tehMick et Ofri pour votre aide!
JS