Générer un labyrinthe de défense de tour ( labyrinthe le plus long avec des murs limités) - heuristique quasi-optimale?
dans un jeu de tower defense, vous avez une grille NxM avec un départ, une arrivée, et un certain nombre de murs.
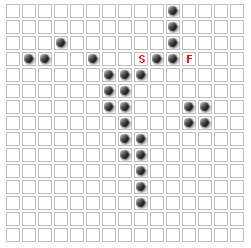
les ennemis prennent le chemin le plus court du début à la fin sans passer par les murs (ils ne sont généralement pas contraints à la grille, mais pour des raisons de simplicité disons qu'ils sont. Dans les deux cas, ils ne peuvent pas se déplacer à travers les "trous" diagonaux)
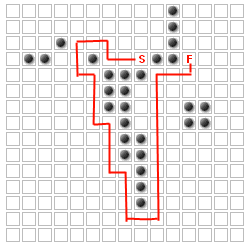
Le problème (pour cette question, au moins) est de placer des jusqu'à K des murs supplémentaires afin de maximiser le chemin les ennemis ont à prendre. Par exemple, pour K=14
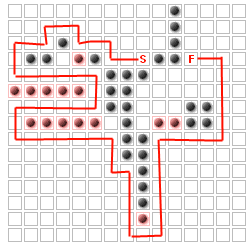
mon intuition me dit que ce problème est NP-dur si (comme j'espère le faire) Nous généralisons cela pour inclure des points de cheminement qui doivent être visités avant de passer à la finition, et peut-être aussi sans waypoints.
mais, y a-t-il des heuristiques décentes là-bas pour des solutions quasi-optimales?
[Edit] j'ai posté une question connexe ici .
8 réponses
il est facile de montrer (preuve faite comme un exercice au lecteur) qu'il suffit de chercher la solution pour que chacun des blocages K soit mis sur la route actuelle de longueur minimale. Notez que s'il y a plusieurs routes de longueur minimale, alors toutes doivent être considérées. La raison est que si vous ne mettez pas l'un des blocages restants sur la route de longueur minimale actuelle, alors il ne change pas; par conséquent, vous pouvez mettre le premier blocus disponible sur elle immédiatement pendant rechercher. Cela accélère même une recherche de force brute.
Mais il y a plus d'optimisations. Vous pouvez également toujours décider que vous mettez le prochain blocus de sorte qu'il devienne le premier blocus sur la route de longueur minimum actuelle, c.-à-d. Vous travaillez de sorte que si vous placez le blocus sur la 10ème place sur la route, alors vous marquez les places 1..9 "ouvert en permanence" jusqu'à ce que vous revenir. Ceci sauve encore une fois un nombre exponentiel de carrés à rechercher pendant la recherche de retracking.
vous pouvez alors appliquer des heuristiques pour réduire l'espace de recherche ou pour le réordonner, par exemple d'abord essayer les positions de blocus qui augmentent le plus la longueur de la route actuelle de longueur minimale. Vous pouvez ensuite exécuter l'algorithme de backtracking pour une quantité limitée de temps réel et de choisir la meilleure solution trouvée jusqu'à présent.
je présente une approche avide et il est peut-être proche de l'optimal (mais je n'ai pas pu trouver le facteur d'approximation). L'idée est simple, nous devrions bloquer les cellules qui sont dans critique les endroits du labyrinthe. Ces lieux peuvent aider à mesurer la connectivité de labyrinthe. Nous pouvons considérer la connectivité vertex et nous trouvons la coupure vertex minimum qui déconnecte le départ et le final: (s,f) . Après cela, nous retirons quelques cellules critiques.
pour le transformer en graphe, prenez du dual of maze. Trouver le minimum (s,f) sommet coupé sur ce graphe. Puis, nous examinons chaque sommet de cette coupe. Nous supprimons un sommet sa suppression augmente la longueur de tous les chemins s,f ou si elle est dans le chemin de longueur minimale de s à F. Après avoir éliminé un vertex, répéter récursivement le processus ci-dessus pour k temps.
mais il y a un problème avec cela, c'est quand nous enlevons un vertex qui coupe n'importe quel chemin de s à F. Pour prévenir cela, nous pouvons peser le noeud de coupe aussi haut que possible,signifie d'abord calculer minimum (s, f) Coupe, si le résultat de coupe est juste un noeud, le faire pondéré et mettre un poids élevé comme n^3 à ce vertex,maintenant de nouveau calculer le minimum s, f coupe, seul vertex de coupe dans le calcul précédent n'appartient pas à la nouvelle coupe en raison de l'attente.
mais s'il n'y a qu'un chemin entre s,f (après quelques itérations) nous ne pouvons pas l'améliorer. Dans ce cas, nous pouvons utiliser la normale des algorithmes cupides Comme enlever un noeud d'un chemin le plus court de s à f qui n'appartient à aucune coupure. après ça, on pourra s'occuper de la coupure minimale du vertex.
le temps d'exécution de l'algorithme dans chaque étape est:
min-cut + path finding for all nodes in min-cut
O(min cut) + O(n^2)*O(number of nodes in min-cut)
et parce que le nombre de noeuds dans la coupe min ne peut pas être plus grand que O (N^2) dans la situation très pessimiste l'algorithme est O (k n^4), mais normalement il ne devrait pas prendre plus de O( k n^3), parce que normalement l'algorithme de min-cut domine la recherche de chemin, aussi normalement la recherche de chemin ne prend pas O (N^2).
je suppose que le choix gourmand est un bon point de départ pour simuler des algorithmes de type recuit.
P. S: la coupe minimale du sommet est similaire à la coupe minimale du bord , et une approche similaire comme max-flow / min-cut peut être appliquée sur la coupe minimale du sommet , il suffit de supposer chaque sommet comme deux vertex , one V i , un V o , signifie entrées et sorties , convertir aussi un graphique non dirigé en un graphique dirigé n'est pas difficile.
je crois que nous pouvons réduire le problème contenu multiple maximum à Boolean satisifiability et montrer NP-completeness par toute dépendance sur ce sous-problème. Pour cette raison, les algorithmes spinning_plate fourni sont des heuristiques raisonnables, précomputing et l'apprentissage machine est raisonnable , et l'astuce devient de trouver le meilleur solution heuristique si nous voulons gaffe en avant ici.
considérez une planche comme la suivante:
..S........
#.#..#..###
...........
...........
..........F
cela a beaucoup de problèmes qui causent des solutions cupides et liées à la porte d'échouer. Si nous regardons cette deuxième rangée:
#.#..#..###
nos portes logiques sont, dans un tableau 2D basé sur 0 commandé par [row][column] :
[1][4], [1][5], [1][6], [1][7], [1][8]
On peut refaire le rendu de ce qu'une équation pour satisfaire le bloc:
if ([1][9] AND ([1][10] AND [1][11]) AND ([1][12] AND [1][13]):
traversal_cost = INFINITY; longest = False # Infinity does not qualify
à l'Exception de l'infini en un unsatisfiable cas, nous revenir en arrière et rerender ce que:
if ([1][14] AND ([1][15] AND [1][16]) AND [1][17]:
traversal_cost = 6; longest = True
et notre relation cachée entre booléens tombe entre toutes ces portes. Vous pouvez également montrer que les épreuves géométriques ne peuvent pas se fractaliser de façon récursive, parce que nous pouvons toujours créer un mur qui est exactement N-1 largeur ou hauteur long, et cela représente une partie critique de la solution dans tous les cas (donc, diviser pour mieux régner ne sera pas utile vous.)
en outre, parce que les perturbations à travers lignes différentes sont significatives:
..S........
#.#........
...#..#....
.......#..#
..........F
nous pouvons montrer que, sans un ensemble complet d'identités géométriques calculables, l'espace de recherche complet se réduit à N-SAT.
par extension, on peut aussi montrer que c'est trivial à vérifier et non polynomial à résoudre alors que le nombre de portes approche l'infini. Sans surprise, c'est pourquoi les jeux tower defense restent si amusants pour les humains. Évidemment, une preuve plus rigoureuse est souhaitable, mais c'est un début squelettique.
notez que vous pouvez réduire considérablement le n stage de n-choisissez-k relation. Parce que nous pouvons montrer récursivement que chaque perturbation doit se trouver sur le chemin critique, et parce que le chemin critique est toujours calculable en O (V+E) temps( avec quelques optimisations pour accélérer les choses pour chaque perturbation), vous pouvez réduire considérablement votre espace de recherche à un coût d'une largeur de recherche pour chaque tour supplémentaire ajouté à la carte.
parce que nous pouvons raisonnablement supposer O(N^k) pour une solution déterministe, une approche heuristique est raisonnable. Mon conseil se situe donc quelque part entre réponse de spinning_plate et de Soravux , avec un oeil vers les techniques d'apprentissage machine applicables au problème.
Le 0e solution: Utiliser un tolérable, mais sous-optimale de l'IA, dans lequel spinning_plate fourni deux algorithmes utilisables. En effet, ceux-ci se rapprochent du nombre approximatif de joueurs naïfs approchant le jeu, et cela devrait être suffisant pour un jeu simple, bien qu'avec un haut degré d'exploitabilité.
Le 1er ordre de la solution: Utiliser une base de données. Compte tenu de la formulation du problème, vous n'avez pas tout à fait démontré la nécessité de calculer le solution optimale à la volée. Par conséquent, si nous relâchons la contrainte de l'approche d'un tableau aléatoire sans aucune information, nous pouvons simplement précalculer l'optimum pour tous K tolérable pour chaque tableau. Évidemment, cela ne fonctionne que pour un petit nombre de cartes: avec V! des états de cartes potentiels pour chaque configuration, nous ne pouvons pas raisonnablement précalculer tous les optimums car V devient très grand.
la solution de deuxième ordre: utiliser un étape d'apprentissage à la machine. Promouvoir chaque étape que vous fermez un écart qui se traduit par un coût transversal très élevé, en cours d'exécution jusqu'à ce que votre algorithme converge ou pas de solution plus optimale peut être trouvé que cupide. Une pléthore d'algorithmes sont applicables ici, donc je recommande de poursuivre les classiques et la littérature pour sélectionner le bon qui fonctionne dans les contraintes de votre programme.
Le meilleure heuristique peut être une simple heat map générée par une première traversée récursive, consciente de l'état local, en triant les résultats par la traversée la plus ou la moins fréquente après la traversée O(v^2). Passer à travers cette sortie identifie avidement tous les goulots d'étranglement, et le faire sans rendre la trajectoire impossible est tout à fait possible (vérifier ceci est O(V+E)).
en unissant tout, j'essaierais une intersection de ces approches, la carte de la chaleur et du chemin critique des identités. Je suppose qu'il y en a assez pour trouver une bonne preuve géométrique fonctionnelle qui satisfasse toutes les contraintes du problème.
au risque de dire l'évidence, voici un algorithme
1) Find the shortest path
2) Test blocking everything node on that path and see which one results in the longest path
3) Repeat K times
naïvement, cela prendra O (K*(V+ E log e)^2) mais vous pourriez avec un peu de travail améliorer 2 en ne recalculant que les chemins partiels.
comme vous le mentionnez, simplement essayer de briser le chemin est difficile parce que si la plupart des pauses simplement ajouter une longueur de 1 (ou 2), Il est difficile de trouver les points d'étranglement qui conduisent à de grands gains.
si vous prenez le minimum vertex cut entre le début et la fin, vous trouverez les points d'étranglement pour l'ensemble du graphique. Un algorithme possible est ce
1) Find the shortest path
2) Find the min-cut of the whole graph
3) Find the maximal contiguous node set that intersects one point on the path, block those.
4) Wash, rinse, repeat
3) est la grande partie et pourquoi cet algorithme peut fonctionner mal, aussi. Vous pouvez aussi essayer
- le plus petit ensemble de noeuds qui se connecte avec d'autres blocs existants.
- trouver tous les groupements de vertiges contigus dans la coupure du sommet, tester chacun d'eux pour le chemin le plus long a la le premier algorithme
est La dernière, ce qui pourrait être le plus prometteur
Si vous trouvez un min sommet de coupe sur l'ensemble du graphique, vous allez trouver les points d'étranglement pour l'ensemble du graphique.
Voici une pensée. Dans votre grille, groupez les murs adjacents en îlots et traitez chaque îlot comme un noeud graphique. La Distance entre les noeuds est le nombre minimal de murs nécessaires pour les connecter (pour bloquer l'ennemi).
dans ce cas, vous pouvez commencer à maximiser la longueur du chemin en bloquant les arcs les plus bon marché.
Je n'ai aucune idée si cela pourrait fonctionner, parce que vous pourriez faire de nouvelles îles en utilisant vos points. mais ça pourrait aider à trouver où mettre des murs.
je suggère d'utiliser une première recherche de largeur modifiée avec une file d'attente prioritaire K-length tracking the best K paths between each island.
je voudrais, pour chaque Île de murs connectés, prétendre que c'est une lumière. (une lumière spéciale qui ne peut émettre que des rayons de lumière horizontaux et verticaux)
utilisez le traçage des rayons pour voir quelles autres îles la lumière peut atteindre
dire Island1 (i1) frappe i2,i3,i4,i5, mais ne frappe pas i6,i7..
alors que vous auriez ligne(i1,i2), (i1,i3), (i1,i4) et(i1,i5)
marque la distance de tous les points de grille à l'infini. Mettez le point de départ à 0.
utilisez maintenant la première recherche de largeur dès le début. Chaque point de grille, marquez la distance de ce point de grille à être la distance minimale de ses voisins.
mais.. voici la capture..
chaque fois que vous arrivez à un point de grille qui est sur une ligne () entre deux îles, au lieu d'enregistrer la distance comme le minimum de ses voisins, vous devez en faire une file d'attente prioritaire de longueur K. et enregistrer les K chemins Les plus courts à cette ligne() à partir de l'une des autres lignes () s
ce quèque prioritaire reste le même jusqu'à la ligne suivante (), où il regroupe toutes les questions prioritaires allant dans ce point.
vous n'avez pas montré la nécessité pour cet algorithme d'être en temps réel, mais je peux me tromper à propos de cette prémice. Vous pouvez alors précalculer les positions du bloc.
si vous pouvez faire cela à l'avance et puis tout simplement faire L'AI construire le labyrinthe roche par roche comme si c'était une sorte d'arbre, vous pourriez utiliser des algorithmes génétiques pour faciliter votre besoin de heuristique. Vous auriez besoin de charger tout type d'algorithme génétique cadre, commencer avec une population de blocs non mobiles (votre carte) et blocs mobiles placés au hasard (blocs que l'IA placerait). Ensuite, vous faites évoluer la population en faisant des croisements et des transmutations sur des blocs mobiles, puis vous évaluez les individus en donnant plus de récompense au plus long chemin calculé. Vous auriez alors simplement à écrire une calculatrice de chemin efficace ressource sans avoir besoin d'heuristiques dans votre code. Dans votre dernière génération de votre évolution, vous prendriez l'individu de plus haut rang, ce qui serait votre solution, donc votre modèle de bloc désiré pour cette carte.
les algorithmes génétiques sont prouvés pour vous conduire, dans une situation idéale, à un maximum local (ou minima) dans un délai raisonnable, qui peut être impossible à atteindre avec des solutions analytiques sur un ensemble de données suffisamment grand (c.-à-d. carte assez grande dans votre situation).
vous n'avez pas indiqué le langage dans lequel vous allez développer cet algorithme, donc je ne peux pas proposer des cadres qui peuvent parfaitement adaptés à vos besoins.
notez que si votre carte est dynamique, ce qui signifie que la carte peut changer au-dessus des itérations de défense de tour, vous pouvez vouloir éviter cette technique car il peut être trop intensif pour ré-évoluer une population entière Nouvelle chaque vague.
Je ne suis pas du tout un expert en algorithmes, mais en regardant la grille, je me demande si le jeu de la vie de Conway pourrait être utile pour cela. Avec une graine initiale raisonnable et des règles bien choisies sur la naissance et la mort des tours, vous pourriez essayer de nombreuses graines et les générations suivantes de celui-ci dans une courte période de temps.
vous avez déjà une mesure de fitness dans la longueur du chemin des creeps, de sorte que vous pourriez choisir le meilleur en conséquence. Je ne sais pas comment bien (si), il serait approximatif, le meilleur chemin, mais ce serait une chose intéressante à utiliser dans une solution.