Générer un DAG aléatoire
Je résous un problème sur un graphe acyclique dirigé.
Mais j'ai du mal à tester mon code sur certains graphes acycliques dirigés. Les graphiques de test doivent être grands et (évidemment) acycliques.
J'ai beaucoup essayé d'écrire du code pour générer des graphes dirigés acycliques. Mais j'ai échoué à chaque fois.
Existe-t-il une méthode existante pour générer des graphes dirigés acycliques que je pourrais utiliser?
7 réponses
J'ai concocté un programme C qui fait cela. La clé est de "classer" les nœuds, et seulement dessiner des bords de nœuds de rang inférieur à ceux de rang supérieur.
Le programme que j'ai écrit imprime dans le langage DOT.
Voici le code lui-même, avec des commentaires expliquant ce que cela signifie:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MIN_PER_RANK 1 /* Nodes/Rank: How 'fat' the DAG should be. */
#define MAX_PER_RANK 5
#define MIN_RANKS 3 /* Ranks: How 'tall' the DAG should be. */
#define MAX_RANKS 5
#define PERCENT 30 /* Chance of having an Edge. */
int main (void)
{
int i, j, k,nodes = 0;
srand (time (NULL));
int ranks = MIN_RANKS
+ (rand () % (MAX_RANKS - MIN_RANKS + 1));
printf ("digraph {\n");
for (i = 0; i < ranks; i++)
{
/* New nodes of 'higher' rank than all nodes generated till now. */
int new_nodes = MIN_PER_RANK
+ (rand () % (MAX_PER_RANK - MIN_PER_RANK + 1));
/* Edges from old nodes ('nodes') to new ones ('new_nodes'). */
for (j = 0; j < nodes; j++)
for (k = 0; k < new_nodes; k++)
if ( (rand () % 100) < PERCENT)
printf (" %d -> %d;\n", j, k + nodes); /* An Edge. */
nodes += new_nodes; /* Accumulate into old node set. */
}
printf ("}\n");
return 0;
}
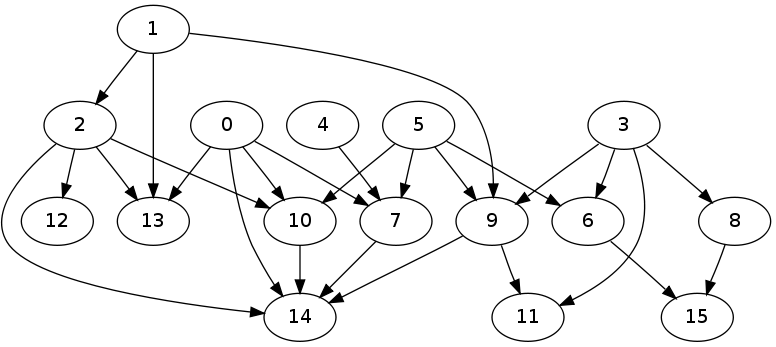
Et voici le graphique généré à partir d'un test:
La réponse à https://mathematica.stackexchange.com/questions/608/how-to-generate-random-directed-acyclic-graphs s'applique: si vous avez une représentation matricielle d'adjacence des bords de votre graphe, alors si la matrice est triangulaire inférieure, c'est un DAG par nécessité.
Une approche similaire serait de prendre un arbitraire de la commande de vos nœuds, et d'examiner ensuite les bords du nœud x à y seulement lorsque x . Cette contrainte devrait également obtenir votre DAGness par construction. La comparaison de la mémoire serait un moyen arbitraire d'ordonner vos nœuds si vous utilisez des structures pour représenter les nœuds.
, Fondamentalement, le pseudocode serait quelque chose comme:
for(i = 0; i < N; i++) {
for (j = i+1; j < N; j++) {
maybePutAnEdgeBetween(i, j);
}
}
Où N est le nombre de nœuds dans votre graphique.
Le pseudocode suggère que le nombre de Dag potentiels, étant donné N nœuds, est
2^(n*(n-1)/2),
Puisqu'il y a
n*(n-1)/2
Paires ordonnées ("n choisissez 2"), et nous pouvons choisir soit d'avoir l'avantage entre eux ou non.
Vous pouvez générer un graphe dirigé aléatoire, puis effectuer une recherche approfondie des cycles. Lorsque vous trouvez un cycle, cassez-le en supprimant un bord.
Je pense que c'est le pire des cas O (VE). Chaque DFS prend O (V) , et chacun supprime au moins un bord (donc Max E)
Si vous générez le graphe dirigé en sélectionnant uniformément au hasard tous les v ^ 2 bords possibles, et que vous DFS dans un ordre aléatoire et supprimez un bord aléatoire-cela vous donnerait une distribution uniforme (ou au moins proche de celle-ci) sur tous les dags possibles.
Donc, pour essayer de rassembler toutes ces réponses raisonnables:
(Dans la suite, j'ai utilisé V pour le nombre de sommets dans le graphique généré, et E pour le nombre d'arêtes, et nous supposons que E ≤ V(V-1)/2.)
Personnellement, je pense que la réponse la plus utile est dans un commentaire, par Flavius, qui pointe le code à http://condor.depaul.edu/rjohnson/source/graph_ge.c . ce code est vraiment simple, et il est commodément décrit par un commentaire, que je reproduire:
To generate a directed acyclic graph, we first
generate a random permutation dag[0],...,dag[v-1].
(v = number of vertices.)
This random permutation serves as a topological
sort of the graph. We then generate random edges of the
form (dag[i],dag[j]) with i < j.
En fait, ce que fait le code est de générer le nombre de requêtes d'arêtes en effectuant à plusieurs reprises ce qui suit:
- génère deux nombres dans la plage [0, V);
- les rejeter s'ils sont égaux;
- échangez-les si le premier est plus grand;
- les rejeter si elle les a générés avant.
Le problème avec cette solution est que lorsque E se ferme au nombre maximum D'arêtes V (V-1) / 2, l'algorithme devient de plus en plus lent, parce qu'il doit rejeter de plus en plus d'arêtes. Une meilleure solution serait de faire un vecteur de tous les bords possibles V(V-1)/2; Mélangez-le aléatoirement; et sélectionnez les premiers bords (Bords demandés) dans la liste mélangée.
L'algorithme d'échantillonnage du réservoir nous permet de le faire dans L'espace O (E), puisque nous pouvons déduire les points de terminaison du Kth edge de la valeur de K. Par conséquent, nous n'avons pas besoin de créer le vecteur source. Cependant, il nécessite toujours O (V 2 ) temps.
Alternativement, on peut faire unFisher-Yates shuffle (ou Knuth shuffle, si vous préférez), en s'arrêtant après E itérations. Dans la version de Fy shuffle présentée dans Wikipedia, cela produira les entrées de fin, mais l'algorithme fonctionne tout aussi bien en arrière:
// At the end of this snippet, a consists of a random sample of the
// integers in the half-open range [0, V(V-1)/2). (They still need to be
// converted to pairs of endpoints).
vector<int> a;
int N = V * (V - 1) / 2;
for (int i = 0; i < N; ++i) a.push_back(i);
for (int i = 0; i < E; ++i) {
int j = i + rand(N - i);
swap(a[i], a[j]);
a.resize(E);
Cela ne nécessite que du temps O(E) mais cela nécessite O (N2) l'espace. En fait, cela peut être amélioré à l'espace O (E) avec une ruse, mais un extrait de code SO est trop petit pour contenir le résultat, je vais donc en fournir un plus simple dans L'espace O(E) et le temps o (e log E). Je suppose qu'il y a une classe DAG avec au moins:
class DAG {
// Construct an empty DAG with v vertices
explicit DAG(int v);
// Add the directed edge i->j, where 0 <= i, j < v
void add(int i, int j);
};
Maintenant, voici:
// Return a randomly-constructed DAG with V vertices and and E edges.
// It's required that 0 < E < V(V-1)/2.
template<typename PRNG>
DAG RandomDAG(int V, int E, PRNG& prng) {
using dist = std::uniform_int_distribution<int>;
// Make a random sample of size E
std::vector<int> sample;
sample.reserve(E);
int N = V * (V - 1) / 2;
dist d(0, N - E); // uniform_int_distribution is closed range
// Random vector of integers in [0, N-E]
for (int i = 0; i < E; ++i) sample.push_back(dist(prng));
// Sort them, and make them unique
std::sort(sample.begin(), sample.end());
for (int i = 1; i < E; ++i) sample[i] += i;
// Now it's a unique sorted list of integers in [0, N-E+E-1]
// Randomly shuffle the endpoints, so the topological sort
// is different, too.
std::vector<int> endpoints;
endpoints.reserve(V);
for (i = 0; i < V; ++i) endpoints.push_back(i);
std::shuffle(endpoints.begin(), endpoints.end(), prng);
// Finally, create the dag
DAG rv;
for (auto& v : sample) {
int tail = int(0.5 + sqrt((v + 1) * 2));
int head = v - tail * (tail - 1) / 2;
rv.add(head, tail);
}
return rv;
}
Une approche très simple est:
Attribuer aléatoirement des arêtes en itérant sur les indices d'une matrice diagonale inférieure (comme suggéré par un lien ci-dessus: https://mathematica.stackexchange.com/questions/608/how-to-generate-random-directed-acyclic-graphs)
Cela vous donnera un DAG avec éventuellement plus d'un composant. Vous pouvez utiliser une structure de données Disjoint-set pour vous donner les composants qui peuvent ensuite être fusionnés en créant des arêtes entre composant.
Les ensembles disjoints sont décrits ici: https://en.wikipedia.org/wiki/Disjoint-set_data_structure
Créer un graphique avec n nœuds et une arête entre chaque paire de nœuds n1 et n2 si n1 != n2 et n2 % n1 == 0.
J'ai récemment essayé de ré-implémenter la réponse acceptée et j'ai trouvé qu'elle était indéterministe. Si vous n'appliquez pas le paramètre min_per_rank, vous pourriez vous retrouver avec un graphique avec 0 nœuds.
Pour éviter cela, j'ai enveloppé les boucles for dans une fonction, puis vérifié pour m'assurer que, après chaque rang, min_per_rank était satisfait. Voici L'implémentation JavaScript:
Https://github.com/karissa/random-dag
Et un code pseudo-C qui remplacerait le code accepté boucle principale de la réponse.
int pushed = 0
int addRank (void)
{
for (j = 0; j < nodes; j++)
for (k = 0; k < new_nodes; k++)
if ( (rand () % 100) < PERCENT)
printf (" %d -> %d;\n", j, k + nodes); /* An Edge. */
if (pushed < min_per_rank) return addRank()
else pushed = 0
return 0
}