Générer des nombres aléatoires suivant une distribution normale en C/C++

EDIT: Depuis le 12 août 2011 nous avons C++11 qui propose directementstd::normal_distribution, c'est comme ça que j'irais aujourd'hui.

Voici la réponse originale:

Voici quelques solutions classées par complexité ascendante.

1. Ajouter 12 nombres uniformes de 0 à 1 et soustraire 6. Ceci correspondra à la moyenne et l'écart type d'une variable normale. Un inconvénient évident est que la plage est limitée à + / -6-contrairement à une vraie normale distribution.

2. Box-Muller transform - a été répertorié ci-dessus, et est relativement simple à mettre en œuvre. Cependant, si vous avez besoin d'échantillons très précis, sachez que la transformation Box-Muller combinée à certains générateurs uniformes souffre d'une anomalie appelée effet Neave.

   La transformation de Box-Muller avec des générateurs de nombres pseudo-aléatoires congruentiels multiplicatifs, " Applied Statistics, 22, 92-97, 1973

3. Pour meilleur précision {[19] } je suggère de dessiner des uniformes et d'appliquer la distribution normale cumulative inverse pour arriver à des variables normalement distribuées. Vous pouvez trouver un très bon algorithme pour la distribution normale cumulative inverse à

Https://web.archive.org/web/20151030215612/http://home.online.no/~pjacklam/notes/invnorm/

Espérons que cela aide

Peter

Une méthode rapide et facile consiste simplement à additionner un nombre de nombres aléatoires répartis uniformément et à prendre leur moyenne. Voir le Central Limit Theorem pour une explication complète de pourquoi cela fonctionne.

J'ai créé un projet open source C++ pour le benchmark de génération de nombres aléatoires normalement distribué .

Il compare plusieurs algorithmes, y compris

• méthode du théorème de la limite centrale
• transformation Box-Muller
• Marsaglia méthode polaire
• algorithme de Ziggurat
• méthode d'échantillonnage par transformation Inverse.
• cpp11random utilise C++11 std::normal_distribution avec std::minstd_rand (c'est en fait une transformation Box-Muller dans clang).

Les résultats de version simple précision (float) sur iMac Corei5-3330S@2.70GHz , clang 6.1, 64 bits:

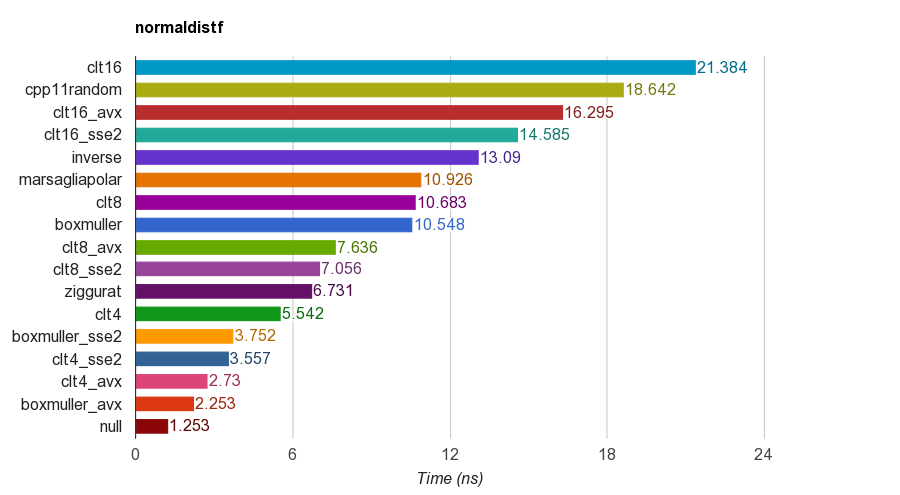
Pour l'exactitude, le programme vérifie la moyenne, l'écart-type, l'asymétrie et la kurtose des échantillons. Il a été constaté que la méthode CLT en additionnant 4, 8 ou 16 nombres uniformes n'ont pas de bonne kurtosis que les autres méthodes.

L'algorithme de Ziggurat a de meilleures performances que les autres. Cependant, il ne convient pas au parallélisme SIMD car il a besoin de recherche de table et de branches. Box-Muller avec SSE2 / AVX jeu d'instructions est beaucoup plus rapide (x1. 79, x2.99) que la version non-SIMD de l'algorithme ziggurat.

Par conséquent, je vais suggérer d'utiliser Box-Muller pour l'architecture avec des jeux D'instructions SIMD, et peut être Ziggurat autrement.

P.S. le benchmark utilise un PRNG LCG le plus simple pour générer des nombres aléatoires distribués uniformes. Il peut donc ne pas être suffisant pour certaines applications. Mais la comparaison des performances devrait être juste car toutes les implémentations utilisent la même chose PRNG, donc le benchmark teste principalement la performance de la transformation.

Voici un exemple C++, basé sur certaines références. C'est rapide et sale, il vaut mieux ne pas réinventer et utiliser la bibliothèque boost.

#include "math.h" // for RAND, and rand
double sampleNormal() {
    double u = ((double) rand() / (RAND_MAX)) * 2 - 1;
    double v = ((double) rand() / (RAND_MAX)) * 2 - 1;
    double r = u * u + v * v;
    if (r == 0 || r > 1) return sampleNormal();
    double c = sqrt(-2 * log(r) / r);
    return u * c;
}

Vous pouvez utiliser un diagramme Q-Q pour examiner les résultats et voir à quel point il se rapproche d'une distribution normale réelle (classez vos échantillons 1..x, transformer les rangs en proportions du nombre total de x ie. combien d'échantillons, obtenez les valeurs z et tracez-les. Une ligne droite vers le haut est le résultat souhaité).

Utilisez std::tr1::normal_distribution.

L'espace de noms std::tr1 ne fait pas partie de boost. C'est l'espace de noms qui contient les ajouts de bibliothèque du rapport technique C++ 1 et est disponible dans les compilateurs Microsoft et gcc à jour, indépendamment de boost.

C'est ainsi que vous générez les échantillons sur un compilateur C++ moderne.

#include <random>
...
std::mt19937 generator;
double mean = 0.0;
double stddev  = 1.0;
std::normal_distribution<double> normal(mean, stddev);
cerr << "Normal: " << normal(generator) << endl;

Vous pouvez utiliser le GSL. Certains exemples complets sont donnés pour montrer comment l'utiliser.

Jetez un oeil sur: http://www.cplusplus.com/reference/random/normal_distribution/. c'est le moyen le plus simple de produire des distributions normales.

Si vous utilisez C++11, Vous pouvez utiliser std::normal_distribution:

#include <random>

std::default_random_engine generator;
std::normal_distribution<double> distribution(/*mean=*/0.0, /*stddev=*/1.0);

double randomNumber = distribution(generator);

Il existe de nombreuses autres distributions que vous pouvez utiliser pour transformer la sortie de nombres aléatoires moteur.

J'ai suivi la définition du PDF donnée dans http://www.mathworks.com/help/stats/normal-distribution.html et est venu avec ceci:

const double DBL_EPS_COMP = 1 - DBL_EPSILON; // DBL_EPSILON is defined in <limits.h>.
inline double RandU() {
    return DBL_EPSILON + ((double) rand()/RAND_MAX);
}
inline double RandN2(double mu, double sigma) {
    return mu + (rand()%2 ? -1.0 : 1.0)*sigma*pow(-log(DBL_EPS_COMP*RandU()), 0.5);
}
inline double RandN() {
    return RandN2(0, 1.0);
}

Ce n'est peut-être pas la meilleure approche, mais c'est assez simple.

Implémentation de Box-Muller:

#include <cstdlib>
#include <cmath>
#include <ctime>
#include <iostream>
using namespace std;
 // return a uniformly distributed random number
double RandomGenerator()
{
  return ( (double)(rand()) + 1. )/( (double)(RAND_MAX) + 1. );
}
 // return a normally distributed random number
double normalRandom()
{
  double y1=RandomGenerator();
  double y2=RandomGenerator();
  return cos(2*3.14*y2)*sqrt(-2.*log(y1));
}

int main(){
double sigma = 82.;
double Mi = 40.;
  for(int i=0;i<100;i++){
double x = normalRandom()*sigma+Mi;
    cout << " x = " << x << endl;
  }
  return 0;
}

1) la manière graphiquement intuitive de générer des nombres aléatoires gaussiens est d'utiliser quelque chose de similaire à la méthode de Monte Carlo. Vous généreriez un point aléatoire dans une boîte autour de la courbe gaussienne en utilisant votre générateur de nombres pseudo-aléatoires en C. Vous pouvez calculer si ce point est à l'intérieur ou sous la distribution gaussienne en utilisant l'équation de la distribution. Si ce point est à l'intérieur de la distribution gaussienne, alors vous avez votre nombre aléatoire gaussien comme valeur x du point.

Cette méthode n'est pas parfaite car techniquement la courbe gaussienne continue vers l'infini, et vous ne pouvez pas créer une boîte qui approche l'infini dans la dimension X. Mais la courbe de Guassian se rapproche de 0 dans la dimension y assez rapidement, donc je ne m'inquiéterais pas à ce sujet. La contrainte de la taille de vos variables en C peut être plus un facteur limitant votre précision.

2) Une autre façon serait d'utiliser le théorème de la limite centrale qui stipule que lorsque des variables aléatoires indépendantes sont ajoutés, ils forment une distribution normale. En gardant ce théorème à l'Esprit, vous pouvez approximer un nombre aléatoire gaussien en ajoutant une grande quantité de variables aléatoires indépendantes.

Ces méthodes ne sont pas les plus pratiques, mais cela est à prévoir lorsque vous ne voulez pas utiliser une bibliothèque préexistante. Gardez à l'esprit que cette réponse vient de quelqu'un avec peu ou pas d'expérience en calcul ou en statistique.

Jetez un oeil à ce que j'ai trouvé.

Cette bibliothèque utilise L'algorithme Ziggurat.

Le comp .lang.C FAQ list partage trois façons différentes de générer facilement des nombres aléatoires avec une distribution gaussienne.

Vous pouvez y jeter un oeil: http://c-faq.com/lib/gaussian.html

Il existe différents algorithmes pour la distribution normale cumulative inverse. Les plus populaires en finance quantitative sont testés sur http://chasethedevil.github.io/post/monte-carlo--inverse-cumulative-normal-distribution/

En outre, il montre l'inconvénient des approches de type Ziggurat.

L'ordinateur est un périphérique déterministe. Il n'y a pas de hasard dans le calcul. De plus, le dispositif arithmétique en CPU peut évaluer summ sur un ensemble fini de nombres entiers (effectuer une évaluation en champ fini) et un ensemble fini de nombres rationnels réels. Et a également effectué des opérations au niveau du BIT. Math prend un accord avec plus de grands ensembles comme [0.0, 1.0] avec un nombre infini de points.

Vous pouvez écouter du fil à l'intérieur de l'ordinateur avec un contrôleur, mais aurait-il des distributions uniformes? Je ne sais pas. Mais si on suppose que son signal est le résultat d'accumuler des valeurs énorme quantité de variables aléatoires indépendantes, alors vous recevrez une variable aléatoire distribuée approximativement normale (cela a été prouvé dans la théorie des probabilités)

Il existe des algorithmes appelés - pseudo générateur aléatoire. Comme je l'ai senti le but du générateur pseudo aléatoire est d'émuler le hasard. Et les critères de goodnes est: - la distribution empirique est convergente (en quelque sorte - pointwise, uniforme, L2) à la théorie de l' - les valeurs que vous recevez du générateur aléatoire semblent être idependent. Bien sûr, ce n'est pas vrai du "point de vue réel", mais nous supposons que c'est vrai.

L'une des méthodes populaires - vous pouvez summ 12 I. R. V avec des distributions uniformes....Mais pour être honnête pendant le théorème de limite centrale de dérivation avec l'aide de la Transformée de Fourier, série de Taylor, il est nécessaire d'avoir des hypothèses n->+inf deux fois. donc, par exemple théoriquement-personnellement, je ne sous-estime pas comment les gens effectuer un summ de 12 I. R. V. avec une distribution uniforme.

J'avais la théorie de la probilité à l'Université. Et particulièrement pour moi, il est juste une question de mathématiques. À l'université, j'ai vu le modèle suivant:

double generateUniform(double a, double b)
{
  return uniformGen.generateReal(a, b);
}

double generateRelei(double sigma)
{
  return sigma * sqrt(-2 * log(1.0 - uniformGen.generateReal(0.0, 1.0 -kEps)));
}
double generateNorm(double m, double sigma)
{
  double y2 = generateUniform(0.0, 2 * kPi);
  double y1 = generateRelei(1.0);
  double x1 = y1 * cos(y2);
  return sigma*x1 + m;
}

Une telle façon comment faire c'était juste un exemple, je suppose qu'il existe d'autres façons de l'implémenter.

Provement qu'il est correct peut être trouvé dans ce livre "Moscou, BMSTU, 2004: XVI théorie des probabilités, exemple 6.12, p. 246-247 "de Krishchenko Alexander Petrovitch ISBN 5-7038-2485-0

Malheureusement je ne connais pas l'existence de la traduction de ce livre en anglais.