Générer une heatmap dans MatPlotLib à l'aide d'un jeu de données scatter
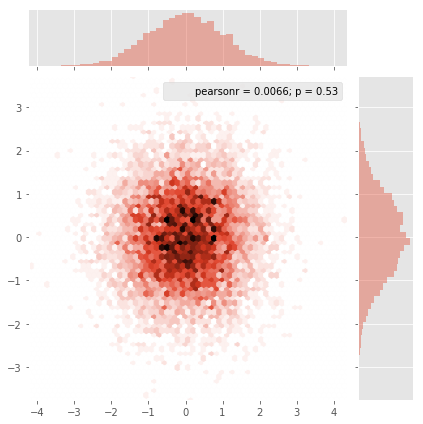
J'ai un ensemble de points de données X,Y (environ 10k) qui sont faciles à tracer comme un nuage de points mais que je voudrais représenter comme une heatmap.
J'ai regardé à travers les exemples dans MatPlotLib et ils semblent tous commencer déjà avec des valeurs de cellules heatmap pour générer l'image.
Existe-t-il une méthode qui convertit un tas de x,y, tous différents, en une heatmap (où les zones avec une fréquence plus élevée de x,y seraient "plus chaudes")?
8 réponses
Si vous ne voulez pas d'hexagones, vous pouvez utiliser la fonction histogram2d de numpy:
import numpy as np
import numpy.random
import matplotlib.pyplot as plt
# Generate some test data
x = np.random.randn(8873)
y = np.random.randn(8873)
heatmap, xedges, yedges = np.histogram2d(x, y, bins=50)
extent = [xedges[0], xedges[-1], yedges[0], yedges[-1]]
plt.clf()
plt.imshow(heatmap.T, extent=extent, origin='lower')
plt.show()
Cela fait une heatmap 50x50. Si vous voulez, par exemple, 512x384, vous pouvez mettre bins=(512, 384) dans l'appel de histogram2d.
Exemple: 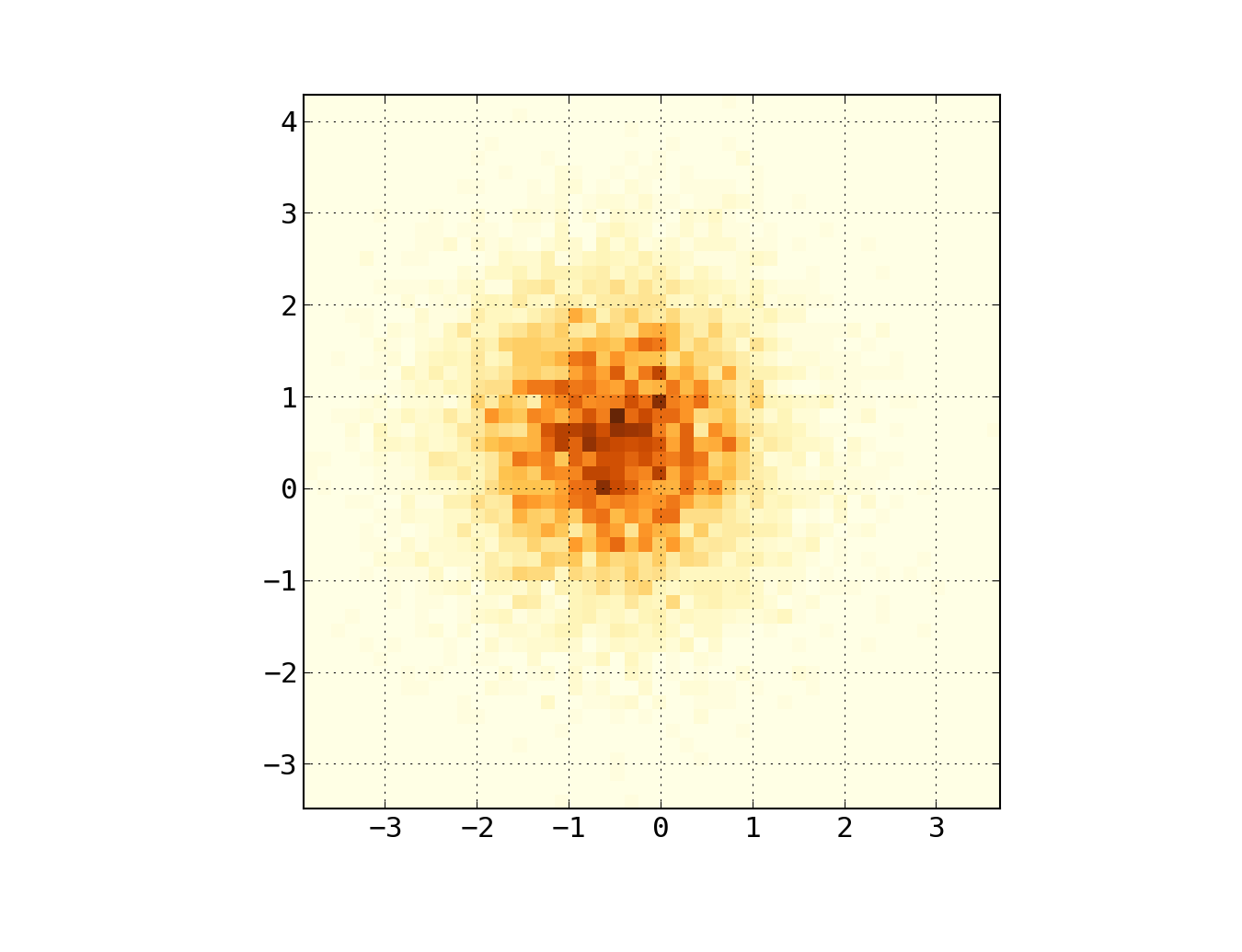
Dans Matplotlib lexique, je pense que vous voulez un hexbin parcelle.
Si vous n'êtes pas familier avec ce type de tracé, c'est juste un histogramme bivarié dans lequel le plan xy est tessellé par une grille régulière d'hexagones.
Ainsi, à partir d'un histogramme, vous pouvez simplement compter le nombre de points tombant dans chaque hexagone, discrétiser la région de traçage comme un ensemble de windows , assigner chaque point à l'une de ces fenêtres; enfin, mapper les fenêtres sur une couleur array , et vous avez un diagramme hexbin.
Bien que moins couramment utilisé que, par exemple, les cercles ou les carrés, que les hexagones sont un meilleur choix pour la géométrie du conteneur binning est intuitive:
-
Les hexagones ont la symétrie du voisin le plus proche (par exemple, les bacs carrés ne le font pas, par exemple, la distance de un point sur la bordure d'un carré à un point à l'intérieur de ce carré n'est pas partout égal) et
Hexagone est le N-polygone le plus élevé qui donne plan régulier tessellation (c'est-à-dire que vous pouvez modéliser en toute sécurité votre plancher de cuisine avec des carreaux de forme hexagonale car vous n'aurez aucun espace vide entre les carreaux lorsque vous aurez terminé-ce qui n'est pas vrai pour tous les autres polygones supérieurs-n, n >= 7).
(Matplotlib utilise le terme hexbin plot; alors faites (AFAIK) toutes les bibliothèques de traçage pour R ; Je ne sais toujours pas si c'est le terme généralement accepté pour les tracés de ce type, bien que je soupçonnez il est probable étant donné que hexbin " est l'abréviation de hexagonale binning, ce qui est décrit l'étape essentielle de la préparation des données pour l'affichage.)
from matplotlib import pyplot as PLT
from matplotlib import cm as CM
from matplotlib import mlab as ML
import numpy as NP
n = 1e5
x = y = NP.linspace(-5, 5, 100)
X, Y = NP.meshgrid(x, y)
Z1 = ML.bivariate_normal(X, Y, 2, 2, 0, 0)
Z2 = ML.bivariate_normal(X, Y, 4, 1, 1, 1)
ZD = Z2 - Z1
x = X.ravel()
y = Y.ravel()
z = ZD.ravel()
gridsize=30
PLT.subplot(111)
# if 'bins=None', then color of each hexagon corresponds directly to its count
# 'C' is optional--it maps values to x-y coordinates; if 'C' is None (default) then
# the result is a pure 2D histogram
PLT.hexbin(x, y, C=z, gridsize=gridsize, cmap=CM.jet, bins=None)
PLT.axis([x.min(), x.max(), y.min(), y.max()])
cb = PLT.colorbar()
cb.set_label('mean value')
PLT.show()
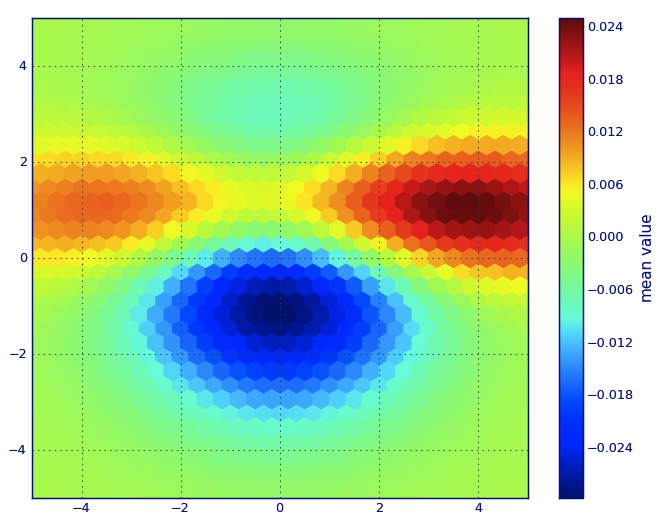
Au lieu d'utiliser np.hist2d, qui en général produit des histogrammes assez laids, je voudrais recycler PY-sphviewer , un paquet python pour rendre des simulations de particules en utilisant un noyau de lissage adaptatif et qui peut être facilement installé à partir de pip (voir la documentation de la page Web). Considérons le code suivant, qui est basé sur l'exemple:
import numpy as np
import numpy.random
import matplotlib.pyplot as plt
import sphviewer as sph
def myplot(x, y, nb=32, xsize=500, ysize=500):
xmin = np.min(x)
xmax = np.max(x)
ymin = np.min(y)
ymax = np.max(y)
x0 = (xmin+xmax)/2.
y0 = (ymin+ymax)/2.
pos = np.zeros([3, len(x)])
pos[0,:] = x
pos[1,:] = y
w = np.ones(len(x))
P = sph.Particles(pos, w, nb=nb)
S = sph.Scene(P)
S.update_camera(r='infinity', x=x0, y=y0, z=0,
xsize=xsize, ysize=ysize)
R = sph.Render(S)
R.set_logscale()
img = R.get_image()
extent = R.get_extent()
for i, j in zip(xrange(4), [x0,x0,y0,y0]):
extent[i] += j
print extent
return img, extent
fig = plt.figure(1, figsize=(10,10))
ax1 = fig.add_subplot(221)
ax2 = fig.add_subplot(222)
ax3 = fig.add_subplot(223)
ax4 = fig.add_subplot(224)
# Generate some test data
x = np.random.randn(1000)
y = np.random.randn(1000)
#Plotting a regular scatter plot
ax1.plot(x,y,'k.', markersize=5)
ax1.set_xlim(-3,3)
ax1.set_ylim(-3,3)
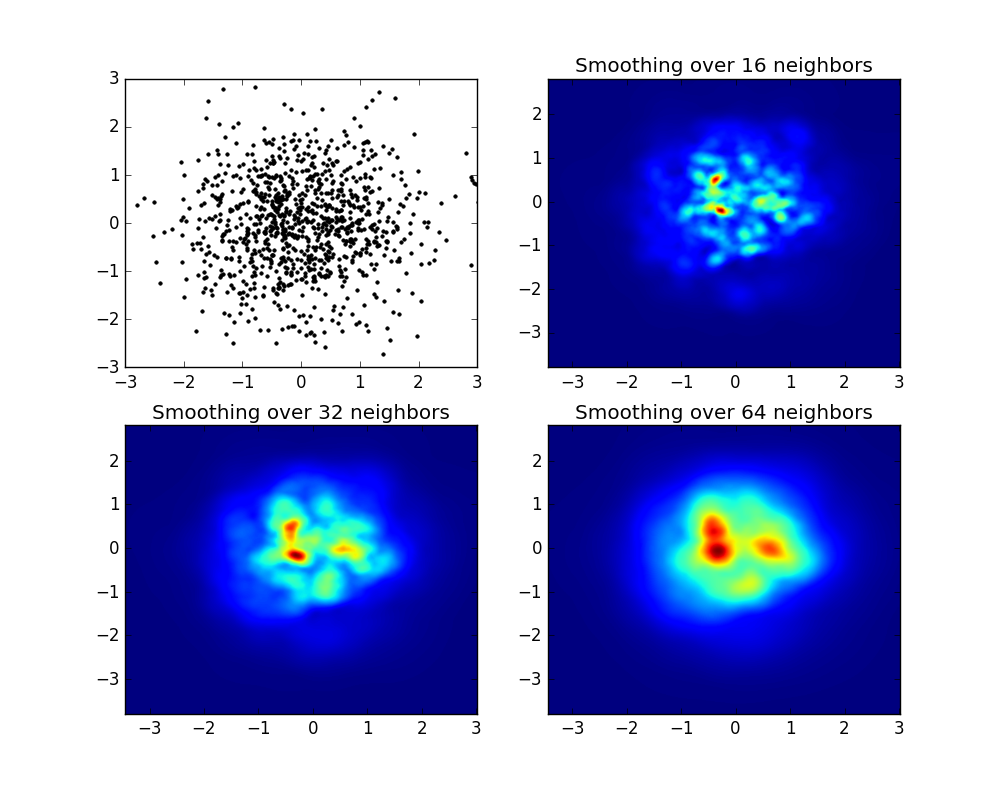
heatmap_16, extent_16 = myplot(x,y, nb=16)
heatmap_32, extent_32 = myplot(x,y, nb=32)
heatmap_64, extent_64 = myplot(x,y, nb=64)
ax2.imshow(heatmap_16, extent=extent_16, origin='lower', aspect='auto')
ax2.set_title("Smoothing over 16 neighbors")
ax3.imshow(heatmap_32, extent=extent_32, origin='lower', aspect='auto')
ax3.set_title("Smoothing over 32 neighbors")
#Make the heatmap using a smoothing over 64 neighbors
ax4.imshow(heatmap_64, extent=extent_64, origin='lower', aspect='auto')
ax4.set_title("Smoothing over 64 neighbors")
plt.show()
Qui produit l'image suivante:
Comme vous le voyez, les images sont plutôt belles, et nous sommes en mesure pour identifier différentes sous-structures sur elle. Ces images sont construites en étalant un poids donné pour chaque point dans un certain domaine, défini par la longueur de lissage, qui est donnée tour à tour par la distance au voisin nb (j'ai choisi 16, 32 et 64 pour les exemples). Ainsi, les régions à densité plus élevée sont généralement réparties sur des régions plus petites par rapport aux régions à densité plus faible.
La fonction myplot est juste une fonction très simple que j'ai écrite pour donner les données x,y à PY-sphviewer pour faire la magie.
Si vous utilisez 1.2.x
x = randn(100000) y = randn(100000) hist2d(x,y,bins=100);
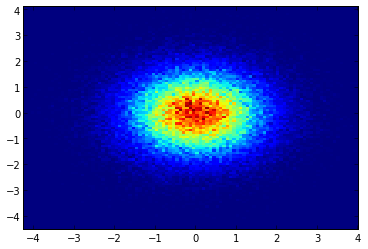
Edit: pour une meilleure approximation de la réponse D'Alejandro, voir ci-dessous.
Je sais que c'est une vieille question, mais je voulais ajouter quelque chose à L'anwser D'Alejandro: si vous voulez une belle image lissée sans utiliser PY-sphviewer, vous pouvez utiliser {[2] } et appliquer un filtre gaussien (de scipy.ndimage.filters) à la heatmap:
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from scipy.ndimage.filters import gaussian_filter
def myplot(x, y, s, bins=1000):
heatmap, xedges, yedges = np.histogram2d(x, y, bins=bins)
heatmap = gaussian_filter(heatmap, sigma=s)
extent = [xedges[0], xedges[-1], yedges[0], yedges[-1]]
return heatmap.T, extent
fig, axs = plt.subplots(2, 2)
# Generate some test data
x = np.random.randn(1000)
y = np.random.randn(1000)
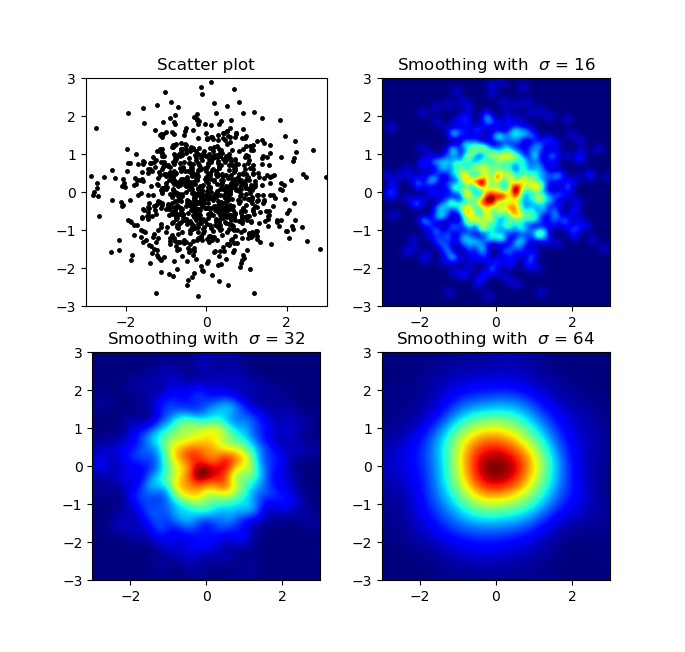
sigmas = [0, 16, 32, 64]
for ax, s in zip(axs.flatten(), sigmas):
if s == 0:
ax.plot(x, y, 'k.', markersize=5)
ax.set_title("Scatter plot")
else:
img, extent = myplot(x, y, s)
ax.imshow(img, extent=extent, origin='lower', cmap=cm.jet)
ax.set_title("Smoothing with $\sigma$ = %d" % s)
plt.show()
Produit:
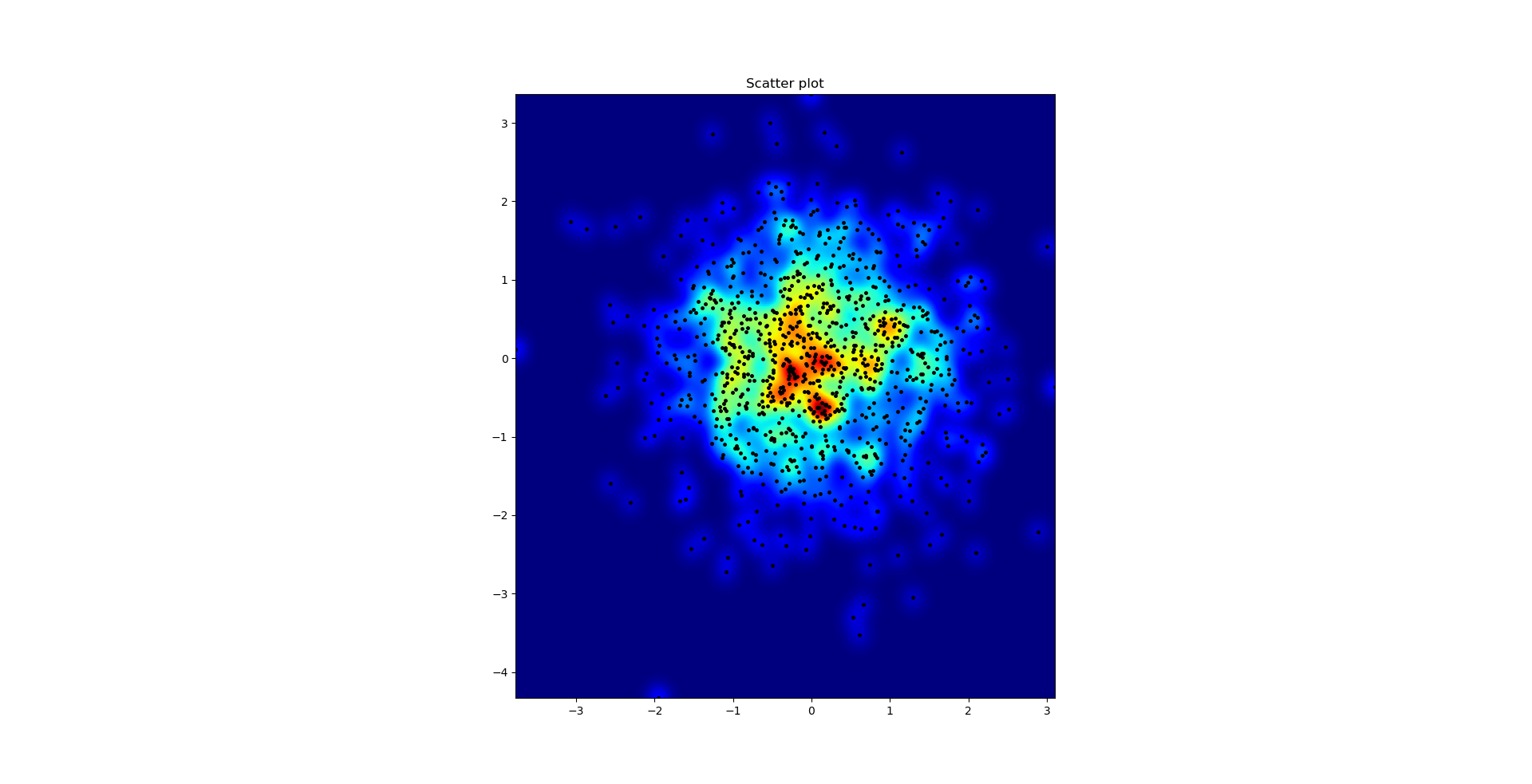
Le diagramme de dispersion et s = 16 tracés les uns sur les autres pour Agape Gal'lo (Cliquez pour mieux voir):
Une différence que j'ai remarquée avec mon approche de filtre gaussien et L'approche D'Alejandro était que sa méthode montre les structures locales beaucoup mieux que la mienne. Par conséquent, j'ai implémenté une méthode simple plus proche voisin au niveau du pixel. Cette méthode calcule pour chaque pixel la somme inverse des distances des n points les plus proches dans les données. Cette méthode est à haute résolution assez coûteuse en calcul et je pense qu'il y a un moyen plus rapide, donc laissez-moi savoir si vous avez des améliorations. Quoi qu'il en soit, voici le code:
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
def data_coord2view_coord(p, vlen, pmin, pmax):
dp = pmax - pmin
dv = (p - pmin) / dp * vlen
return dv
def nearest_neighbours(xs, ys, reso, n_neighbours):
im = np.zeros([reso, reso])
extent = [np.min(xs), np.max(xs), np.min(ys), np.max(ys)]
xv = data_coord2view_coord(xs, reso, extent[0], extent[1])
yv = data_coord2view_coord(ys, reso, extent[2], extent[3])
for x in range(reso):
for y in range(reso):
xp = (xv - x)
yp = (yv - y)
d = np.sqrt(xp**2 + yp**2)
im[y][x] = 1 / np.sum(d[np.argpartition(d.ravel(), n_neighbours)[:n_neighbours]])
return im, extent
n = 1000
xs = np.random.randn(n)
ys = np.random.randn(n)
resolution = 250
fig, axes = plt.subplots(2, 2)
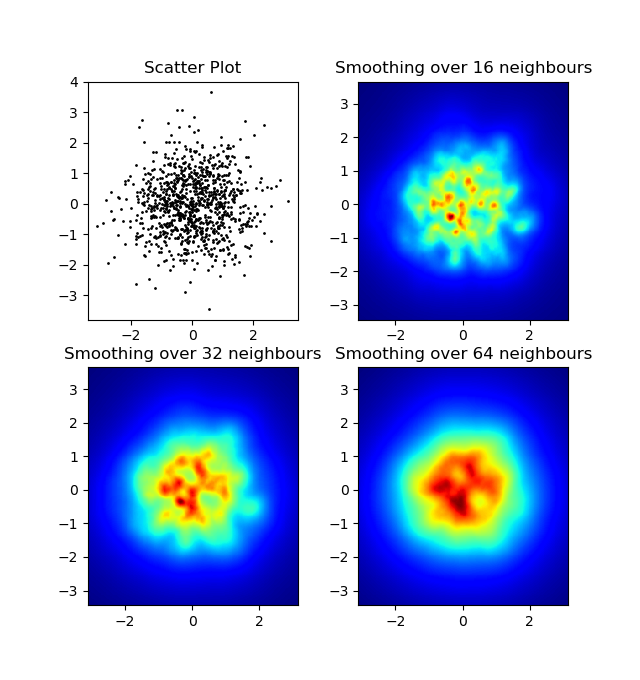
for ax, neighbours in zip(axes.flatten(), [0, 16, 32, 64]):
if neighbours == 0:
ax.plot(xs, ys, 'k.', markersize=2)
ax.set_aspect('equal')
ax.set_title("Scatter Plot")
else:
im, extent = nearest_neighbours(xs, ys, resolution, neighbours)
ax.imshow(im, origin='lower', extent=extent, cmap=cm.jet)
ax.set_title("Smoothing over %d neighbours" % neighbours)
ax.set_xlim(extent[0], extent[1])
ax.set_ylim(extent[2], extent[3])
plt.show()
Résultat:
Seaborn a maintenant la fonction jointplot qui devrait bien fonctionner ici:
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
# Generate some test data
x = np.random.randn(8873)
y = np.random.randn(8873)
sns.jointplot(x=x, y=y, kind='hex')
plt.show()
Créez un tableau à 2 dimensions qui correspond aux cellules de votre image finale, appelé say heatmap_cells et instanciez-le comme tous les zéros.
Choisissez deux facteurs d'échelle qui définissent la différence entre chaque élément de tableau en unités réelles, pour chaque dimension, par exemple x_scale et y_scale. Choisissez-les de sorte que tous vos points de données tombent dans les limites du tableau heatmap.
Pour chaque point de données brut avec x_value et y_value:
heatmap_cells[floor(x_value/x_scale),floor(y_value/y_scale)]+=1
Et la question initiale était... comment convertir les valeurs de dispersion en valeurs de grille, Non?
histogram2d compte la fréquence par cellule, cependant, si vous avez d'autres données par cellule que la fréquence, vous aurez besoin d'un travail supplémentaire à faire.
x = data_x # between -10 and 4, log-gamma of an svc
y = data_y # between -4 and 11, log-C of an svc
z = data_z #between 0 and 0.78, f1-values from a difficult dataset
Donc, j'ai un ensemble de données avec des résultats Z pour les coordonnées X et Y. Cependant, je calculais quelques points en dehors de la zone d'intérêt (grandes lacunes), et des tas de points dans une petite zone d'intérêt.
Oui ici ça devient plus difficile mais aussi plus de plaisir. Quelques bibliothèques (désolé):
from matplotlib import pyplot as plt
from matplotlib import cm
import numpy as np
from scipy.interpolate import griddata
Pyplot est mon moteur graphique aujourd'hui, cm est une gamme de cartes de couleurs avec un choix initeresting. numpy pour les calculs, et griddata pour attacher des valeurs à une grille fixe.
Le dernier est important surtout parce que la fréquence des points xy n'est pas également répartie dans mes données. Tout d'abord, commençons par quelques limites adaptées à mes données et une taille de grille arbitraire. Les données d'origine ont également des points de données en dehors de ceux x et y frontières.
#determine grid boundaries
gridsize = 500
x_min = -8
x_max = 2.5
y_min = -2
y_max = 7
Nous avons donc défini une grille de 500 pixels entre les valeurs min et max de x et Y.
Dans mes données, il y a beaucoup plus que les 500 valeurs disponibles dans la zone d'intérêt élevé; alors que dans la zone à faible intérêt, il n'y a même pas 200 valeurs dans la grille totale; entre les limites graphiques de x_min et x_max Il y en a encore moins.
Donc, pour obtenir une belle image, la tâche est d'obtenir une moyenne pour l'intérêt supérieur de valeurs et de combler les lacunes ailleurs.
Je définis ma grille maintenant. Pour chaque paire xx-yy, je veux avoir une couleur.
xx = np.linspace(x_min, x_max, gridsize) # array of x values
yy = np.linspace(y_min, y_max, gridsize) # array of y values
grid = np.array(np.meshgrid(xx, yy.T))
grid = grid.reshape(2, grid.shape[1]*grid.shape[2]).T
Pourquoi cette forme étrange? scipy.griddata veut une forme de (n, D).
Griddata calcule une valeur par point dans la grille, par une méthode prédéfinie. Je choisis "le plus proche" - les points de grille vides seront remplis avec des valeurs du voisin le plus proche. Cela semble que les zones avec moins d'informations ont des cellules plus grandes (même si ce n'est pas le cas). On pourrait choisir d'interpoler "linéaire", alors les zones avec moins d'informations semblent moins nettes. Question de goût, vraiment.
points = np.array([x, y]).T # because griddata wants it that way
z_grid2 = griddata(points, z, grid, method='nearest')
# you get a 1D vector as result. Reshape to picture format!
z_grid2 = z_grid2.reshape(xx.shape[0], yy.shape[0])
Et hop, nous matplotlib pour afficher l'intrigue
fig = plt.figure(1, figsize=(10, 10))
ax1 = fig.add_subplot(111)
ax1.imshow(z_grid2, extent=[x_min, x_max,y_min, y_max, ],
origin='lower', cmap=cm.magma)
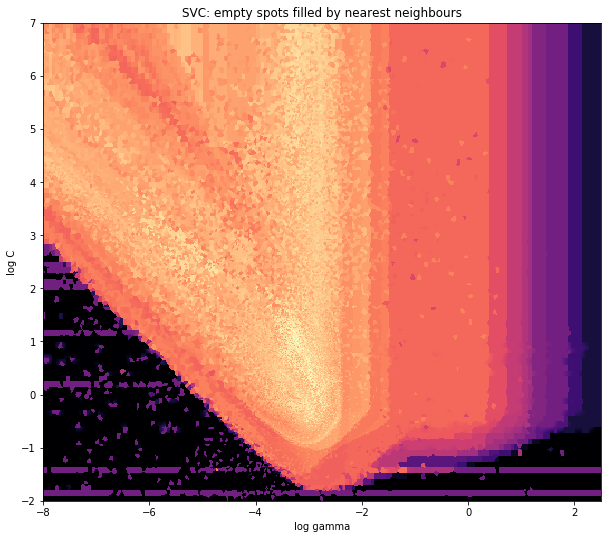
ax1.set_title("SVC: empty spots filled by nearest neighbours")
ax1.set_xlabel('log gamma')
ax1.set_ylabel('log C')
plt.show()
Autour de la partie pointue de la forme en V, vous voyez que j'ai fait beaucoup de calculs lors de ma recherche du sweet spot, alors que les parties les moins intéressantes ont presque partout une résolution inférieure.