Ajustement à l'histogramme de Poisson
j'essaie d'ajuster une courbe sur l'histogramme d'une distribution de Poisson qui ressemble à ceci
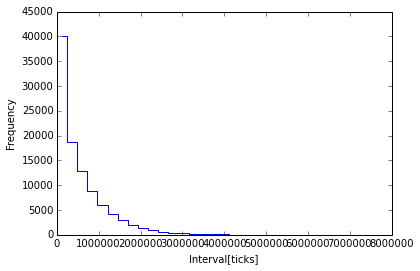
j'ai modifié la fonction fit pour qu'elle ressemble à une distribution de Poisson, avec le paramètre t comme variable. Mais la fonction curve_fit ne peut pas être tracée et je ne sais pas pourquoi.
def histo(bsize):
N = bsize
#binwidth
bw = (dt.max()-dt.min())/(N-1.)
bin1 = dt.min()+ bw*np.arange(N)
#define the array to hold the occurrence count
bincount= np.array([])
for bin in bin1:
count = np.where((dt>=bin)&(dt<bin+bw))[0].size
bincount = np.append(bincount,count)
#bin center
binc = bin1+0.5*bw
plt.figure()
plt.plot(binc,bincount,drawstyle= 'steps-mid')
plt.xlabel("Interval[ticks]")
plt.ylabel("Frequency")
histo(30)
plt.xlim(0,.5e8)
plt.ylim(0,25000)
import numpy as np
from scipy.optimize import curve_fit
delta_t = 1.42e7
def func(x, t):
return t * np.exp(- delta_t/t)
popt, pcov = curve_fit(func, np.arange(0,.5e8),histo(30))
plt.plot(popt)
1 réponses
le problème avec votre code est que vous ne savez pas quelles sont les valeurs de retour de curve_fit. Il s'agit des paramètres de la fonction d'ajustement et de leur matrice de covariance. Pas quelque chose que vous pouvez tracer directement.
Mise À La Poubelle Des Moindres Carrés De L'Ajustement
en général, vous ne pouvez pas obtenir tout beaucoup, beaucoup plus facile:
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
from scipy.misc import factorial
# get poisson deviated random numbers
data = np.random.poisson(2, 1000)
# the bins should be of integer width, because poisson is an integer distribution
entries, bin_edges, patches = plt.hist(data, bins=11, range=[-0.5, 10.5], normed=True)
# calculate binmiddles
bin_middles = 0.5*(bin_edges[1:] + bin_edges[:-1])
# poisson function, parameter lamb is the fit parameter
def poisson(k, lamb):
return (lamb**k/factorial(k)) * np.exp(-lamb)
# fit with curve_fit
parameters, cov_matrix = curve_fit(poisson, bin_middles, entries)
# plot poisson-deviation with fitted parameter
x_plot = np.linspace(0, 20, 1000)
plt.plot(x_plot, poisson(x_plot, *parameters), 'r-', lw=2)
plt.show()
C'est le résultat:
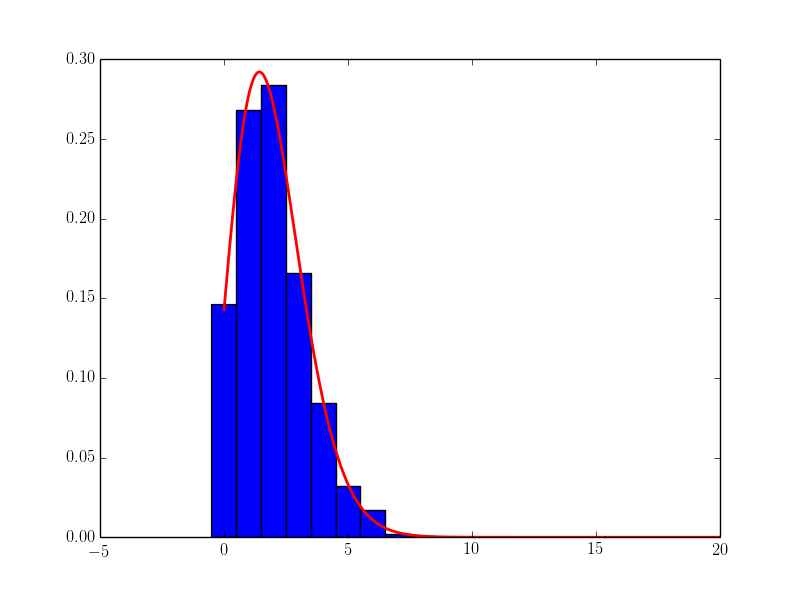
ajustement de vraisemblance maximale non lié
une possibilité encore meilleure serait de ne pas utiliser un histogramme à tous et à la place de faire un ajustement de vraisemblance maximum.
mais en y regardant de plus près, même cela n'est pas nécessaire, parce que le estimateur de vraisemblance maximale pour le paramètre de la distribution poissonienne est la moyenne arithmétique.
cependant, si vous avez d'autres fichiers PDF plus compliqués, vous pouvez utiliser ceci comme exemple:
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize
from scipy.misc import factorial
def poisson(k, lamb):
"""poisson pdf, parameter lamb is the fit parameter"""
return (lamb**k/factorial(k)) * np.exp(-lamb)
def negLogLikelihood(params, data):
""" the negative log-Likelohood-Function"""
lnl = - np.sum(np.log(poisson(data, params[0])))
return lnl
# get poisson deviated random numbers
data = np.random.poisson(2, 1000)
# minimize the negative log-Likelihood
result = minimize(negLogLikelihood, # function to minimize
x0=np.ones(1), # start value
args=(data,), # additional arguments for function
method='Powell', # minimization method, see docs
)
# result is a scipy optimize result object, the fit parameters
# are stored in result.x
print(result)
# plot poisson-deviation with fitted parameter
x_plot = np.linspace(0, 20, 1000)
plt.hist(data, bins=np.arange(15) - 0.5, normed=True)
plt.plot(x_plot, poisson(x_plot, result.x), 'r-', lw=2)
plt.show()