Trouver les chemins entre deux nœuds?
si j'ai des noeuds connectés de la façon ci-dessous, Comment puis-je arriver au nombre de chemins qui existent entre des points donnés, et des détails de chemin?
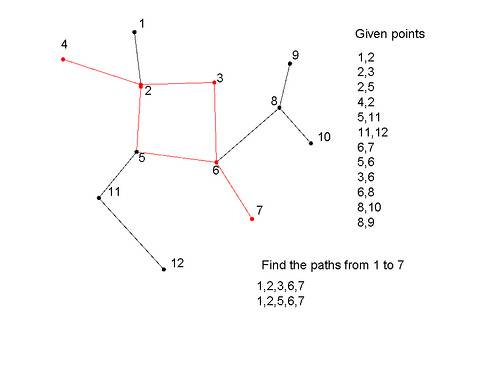
1,2 //node 1 and 2 are connected
2,3
2,5
4,2
5,11
11,12
6,7
5,6
3,6
6,8
8,10
8,9
trouver les chemins de 1 à 7:
réponse: 2 chemins trouvés et ils sont
1,2,3,6,7
1,2,5,6,7
Voici l'extrait du lien ci-dessus en python
# a sample graph
graph = {'A': ['B', 'C','E'],
'B': ['A','C', 'D'],
'C': ['D'],
'D': ['C'],
'E': ['F','D'],
'F': ['C']}
class MyQUEUE: # just an implementation of a queue
def __init__(self):
self.holder = []
def enqueue(self,val):
self.holder.append(val)
def dequeue(self):
val = None
try:
val = self.holder[0]
if len(self.holder) == 1:
self.holder = []
else:
self.holder = self.holder[1:]
except:
pass
return val
def IsEmpty(self):
result = False
if len(self.holder) == 0:
result = True
return result
path_queue = MyQUEUE() # now we make a queue
def BFS(graph,start,end,q):
temp_path = [start]
q.enqueue(temp_path)
while q.IsEmpty() == False:
tmp_path = q.dequeue()
last_node = tmp_path[len(tmp_path)-1]
print tmp_path
if last_node == end:
print "VALID_PATH : ",tmp_path
for link_node in graph[last_node]:
if link_node not in tmp_path:
#new_path = []
new_path = tmp_path + [link_node]
q.enqueue(new_path)
BFS(graph,"A","D",path_queue)
-------------results-------------------
['A']
['A', 'B']
['A', 'C']
['A', 'E']
['A', 'B', 'C']
['A', 'B', 'D']
VALID_PATH : ['A', 'B', 'D']
['A', 'C', 'D']
VALID_PATH : ['A', 'C', 'D']
['A', 'E', 'F']
['A', 'E', 'D']
VALID_PATH : ['A', 'E', 'D']
['A', 'B', 'C', 'D']
VALID_PATH : ['A', 'B', 'C', 'D']
['A', 'E', 'F', 'C']
['A', 'E', 'F', 'C', 'D']
VALID_PATH : ['A', 'E', 'F', 'C', 'D']
8 réponses
Largeur-première recherche traverse un graphe et trouve en fait tous les chemins à partir d'un noeud de départ. Habituellement, BFS ne garde pas tous les chemins, cependant. Au lieu de cela, il met à jour une fonction prédéfinie π pour sauvegarder le chemin le plus court. Vous pouvez facilement modifier l'algorithme de sorte que π(n) ne stocke pas seulement un prédécesseur mais une liste de prédécesseurs possibles.
, Alors tous les chemins possibles sont encodés dans cette fonction, et par en traversant π de façon récursive, vous obtenez toutes les combinaisons de chemins possibles.
un bon pseudocode qui utilise cette notation peut être trouvé dans Introduction aux algorithmes par Cormen et al. et a ensuite été utilisé dans de nombreux scripts universitaires sur le sujet. Une recherche Google pour "BFS pseudocode prédécesseur π "uproots ce hit sur L'échange de pile .
pour ceux qui ne sont pas experts en PYTHON ,le même code en C++
//@Author :Ritesh Kumar Gupta
#include <stdio.h>
#include <vector>
#include <algorithm>
#include <vector>
#include <queue>
#include <iostream>
using namespace std;
vector<vector<int> >GRAPH(100);
inline void print_path(vector<int>path)
{
cout<<"[ ";
for(int i=0;i<path.size();++i)
{
cout<<path[i]<<" ";
}
cout<<"]"<<endl;
}
bool isadjacency_node_not_present_in_current_path(int node,vector<int>path)
{
for(int i=0;i<path.size();++i)
{
if(path[i]==node)
return false;
}
return true;
}
int findpaths(int source ,int target ,int totalnode,int totaledge )
{
vector<int>path;
path.push_back(source);
queue<vector<int> >q;
q.push(path);
while(!q.empty())
{
path=q.front();
q.pop();
int last_nodeof_path=path[path.size()-1];
if(last_nodeof_path==target)
{
cout<<"The Required path is:: ";
print_path(path);
}
else
{
print_path(path);
}
for(int i=0;i<GRAPH[last_nodeof_path].size();++i)
{
if(isadjacency_node_not_present_in_current_path(GRAPH[last_nodeof_path][i],path))
{
vector<int>new_path(path.begin(),path.end());
new_path.push_back(GRAPH[last_nodeof_path][i]);
q.push(new_path);
}
}
}
return 1;
}
int main()
{
//freopen("out.txt","w",stdout);
int T,N,M,u,v,source,target;
scanf("%d",&T);
while(T--)
{
printf("Enter Total Nodes & Total Edges\n");
scanf("%d%d",&N,&M);
for(int i=1;i<=M;++i)
{
scanf("%d%d",&u,&v);
GRAPH[u].push_back(v);
}
printf("(Source, target)\n");
scanf("%d%d",&source,&target);
findpaths(source,target,N,M);
}
//system("pause");
return 0;
}
/*
Input::
1
6 11
1 2
1 3
1 5
2 1
2 3
2 4
3 4
4 3
5 6
5 4
6 3
1 4
output:
[ 1 ]
[ 1 2 ]
[ 1 3 ]
[ 1 5 ]
[ 1 2 3 ]
The Required path is:: [ 1 2 4 ]
The Required path is:: [ 1 3 4 ]
[ 1 5 6 ]
The Required path is:: [ 1 5 4 ]
The Required path is:: [ 1 2 3 4 ]
[ 1 2 4 3 ]
[ 1 5 6 3 ]
[ 1 5 4 3 ]
The Required path is:: [ 1 5 6 3 4 ]
*/
l'algorithme de Dijkstra s'applique plus aux chemins pondérés et on dirait que l'affiche voulait trouver tous les chemins, pas seulement les plus courts.
pour cette application, je construirais un graphique (votre application semble ne pas avoir besoin d'être dirigée) et utiliser votre méthode de recherche préférée. Il semble que vous voulez tous les chemins, pas seulement une conjecture à la plus courte, alors utilisez un algorithme récursif simple de votre choix.
le seul problème est si le graphe peut être cyclique.
avec les raccords:
- 1, 2
- 1, 3
- 2, 3
- 2, 4
en cherchant un chemin de 1 - >4, vous pourriez avoir un cycle de 1 -> 2 -> 3 -> 1.
Dans ce cas, je garderais une pile traversant les nœuds. Voici une liste avec les étapes pour ce graphique et la pile résultante (désolé pour le formatage-pas d'option de table):
noeud courant (noeuds suivants possibles moins l'endroit d'où nous venons) [stack]
- 1 (2, 3) [1]
- 2 (3, 4) [1, 2]
- 3 (1) [1, 2, 3]
- 1 (2, 3) [1, 2, 3, 1] //erreur-numéro de duplicata sur le cycle de cheminée détecté
- 3 () [1, 2, 3] // j'ai fait marche arrière pour le noeud 3 et j'en ai sorti un de la pile. Plus de noeuds à explorer d'ici
- 2 (4) [1, 2] // j'ai fait marche arrière jusqu'au noeud 2 et j'en ai sorti un de la pile.
- 4 () [1, 2, 4] // noeud cible trouvé-empilement d'enregistrement pour un chemin. Plus de noeuds à explorer d'ici
- 2 () [1, 2] //j'ai fait marche arrière jusqu'au noeud 2 et j'en ai sorti 4 de la pile. Plus de noeuds à explorer d'ici
- 1 (3) [1] //j'ai fait marche arrière pour le noeud 1 et j'en ai sorti 2 de la pile.
- 3 (2) [1, 3]
- 2 (1, 4) [1, 3, 2]
- 1 (2, 3) [1, 3, 2, 1] //erreur-numéro de duplicata sur le pile - cycle détecté
- 2 (4) [1, 3, 2] //en arrière-s'avança vers le nœud 2 et sauté 1 hors de la pile
- 4 () [1, 3, 2, 4] noeud cible trouvé-empilement d'enregistrement pour un chemin. Plus de noeuds à explorer d'ici
- 2 () [1, 3, 2] //j'ai fait marche arrière jusqu'au noeud 2 et j'en ai sorti 4 de la pile. Plus de noeuds
- 3 () [1, 3] / / Retour au noeud 3 et sortie 2 de la pile. Plus de noeuds
- 1 () [1] // j'ai fait marche arrière pour le noeud 1 et j'en ai sorti 3 de la pile. Plus de noeuds
- fait avec 2 chemins enregistrés de [1, 2, 4] et [1, 3, 2, 4]
le code original est un peu encombrant et vous pourriez vouloir utiliser les collections.deque à la place si vous voulez utiliser BFS pour trouver si un chemin existe entre 2 points sur le graphe. Voici une solution rapide que j'ai hacké:
Note: cette méthode peut continuer indéfiniment s'il n'existe pas de chemin entre les deux noeuds. Je n'ai pas testé toutes les affaires, YMMV.
from collections import deque
# a sample graph
graph = {'A': ['B', 'C','E'],
'B': ['A','C', 'D'],
'C': ['D'],
'D': ['C'],
'E': ['F','D'],
'F': ['C']}
def BFS(start, end):
""" Method to determine if a pair of vertices are connected using BFS
Args:
start, end: vertices for the traversal.
Returns:
[start, v1, v2, ... end]
"""
path = []
q = deque()
q.append(start)
while len(q):
tmp_vertex = q.popleft()
if tmp_vertex not in path:
path.append(tmp_vertex)
if tmp_vertex == end:
return path
for vertex in graph[tmp_vertex]:
if vertex not in path:
q.append(vertex)
En Prolog (plus précisément, SWI-Prolog)
:- use_module(library(tabling)).
% path(+Graph,?Source,?Target,?Path)
:- table path/4.
path(_,N,N,[N]).
path(G,S,T,[S|Path]) :-
dif(S,T),
member(S-I, G), % directed graph
path(G,I,T,Path).
essai:
paths :- Graph =
[ 1- 2 % node 1 and 2 are connected
, 2- 3
, 2- 5
, 4- 2
, 5-11
,11-12
, 6- 7
, 5- 6
, 3- 6
, 6- 8
, 8-10
, 8- 9
],
findall(Path, path(Graph,1,7,Path), Paths),
maplist(writeln, Paths).
?- paths.
[1,2,3,6,7]
[1,2,5,6,7]
true.
étant donné la matrice de contiguïté:
{0, 1, 3, 4, 0, 0}
{0, 0, 2, 1, 2, 0}
{0, 1, 0, 3, 0, 0}
{0, 1, 1, 0, 0, 1}
{0, 0, 0, 0, 0, 6}
{0, 1, 0, 1, 0, 0}
le code de Wolfram Mathematica suivant résout le problème pour trouver tous les chemins simples entre deux noeuds d'un graphe. J'ai utilisé la récursion simple, et deux var global pour garder la trace des cycles et pour stocker la sortie désirée. le code n'a pas été optimisé juste pour la clarté du code. l '"imprimé" devrait être utile pour clarifier comment il fonctionne.
cycleQ[l_]:=If[Length[DeleteDuplicates[l]] == Length[l], False, True];
getNode[matrix_, node_]:=Complement[Range[Length[matrix]],Flatten[Position[matrix[[node]], 0]]];
builtTree[node_, matrix_]:=Block[{nodes, posAndNodes, root, pos},
If[{node} != {} && node != endNode ,
root = node;
nodes = getNode[matrix, node];
(*Print["root:",root,"---nodes:",nodes];*)
AppendTo[lcycle, Flatten[{root, nodes}]];
If[cycleQ[lcycle] == True,
lcycle = Most[lcycle]; appendToTree[root, nodes];,
Print["paths: ", tree, "\n", "root:", root, "---nodes:",nodes];
appendToTree[root, nodes];
];
];
appendToTree[root_, nodes_] := Block[{pos, toAdd},
pos = Flatten[Position[tree[[All, -1]], root]];
For[i = 1, i <= Length[pos], i++,
toAdd = Flatten[Thread[{tree[[pos[[i]]]], {#}}]] & /@ nodes;
(* check cycles!*)
If[cycleQ[#] != True, AppendTo[tree, #]] & /@ toAdd;
];
tree = Delete[tree, {#} & /@ pos];
builtTree[#, matrix] & /@ Union[tree[[All, -1]]];
];
];
pour appeler le code: initNode = 1; endNode = 6; lcycle = {}; arbre = {{initNode}}; builtTree[initNode, matrix];
chemins: {{1}} racine: 1 - - - noeuds: {2,3,4}
les chemins de: {{1,2},{1,3},{1,4}} racine: 2 - - - noeuds: {3,4,5}
les chemins de: {{1,3},{1,4},{1,2,3},{1,2,4},{1,2,5}} racine: 3 - - - noeuds: {2,4}
les chemins de: {{1,4},{1,2,4},{1,2,5},{1,3,4},{1,2,3,4},{1,3,2,4},{1,3,2,5}} racine: 4 - - - noeuds: {2,3,6}
les chemins de: {{1,2,5},{1,3,2,5},{1,4,6},{1,2,4,6},{1,3,4,6},{1,2,3,4,6},{1,3,2,4,6},{1,4,2,5},{1,3,4,2,5},{1,4,3,2,5}} racine: 5 - - - noeuds: {6}
RÉSULTATS:{{1, 4, 6}, {1, 2, 4, 6}, {1, 2, 5, 6}, {1, 3, 4, 6}, {1, 2, 3, 4, 6}, {1, 3, 2, 4, 6}, {1, 3, 2, 5, 6}, {1, 4, 2, 5, 6}, {1, 3, 4, 2, 5, 6}, {1, 4, 3, 2, 5, 6}}
...Malheureusement je ne peux pas télécharger des images pour montrer les résultats d'une meilleure façon: (
si vous voulez tous les chemins, utilisez recursion.
en utilisant une liste adjacente, de préférence, créer une fonction f() qui tente de remplir une liste courante des sommets visités. Comme ceci:
void allPaths(vector<int> previous, int current, int destination)
{
previous.push_back(current);
if (current == destination)
//output all elements of previous, and return
for (int i = 0; i < neighbors[current].size(); i++)
allPaths(previous, neighbors[current][i], destination);
}
int main()
{
//...input
allPaths(vector<int>(), start, end);
}
en raison du fait que le vecteur est transmis par la valeur (et donc tous les changements apportés plus bas dans la procédure récursive ne sont pas permanents), toutes les combinaisons possibles sont énumérées.
vous pouvez gagner un peu d'efficacité par passer le vecteur précédent par référence (et donc ne pas avoir à copier le vecteur encore et encore) mais vous devrez vous assurer que les choses obtiennent popped_back() manuellement.
encore une chose: si le graphe a des cycles, cela ne marchera pas. (Je suppose que dans ce cas vous voulez trouver tous les chemins simple , puis) avant d'ajouter quelque chose dans le vecteur précédent , Vérifiez d'abord si c'est déjà là.
si vous voulez tous les chemins les plus courts , utilisez la suggestion de Konrad avec cet algorithme.
ce que vous essayez de faire est essentiellement de trouver un chemin entre deux sommets dans un (dirigé?) Graph check out algorithme de Dijkstra si vous avez besoin du chemin le plus court ou écrire une fonction récursive simple si vous avez besoin de n'importe quels chemins existent.