Trouver la plus grande zone noire convexe dans une image
J'ai une image dont c'est une petite découpe:

Comme vous pouvez le voir, ce sont des pixels blancs sur un fond noir. On peut tracer des lignes imaginaires entre ces pixels (ou mieux, des points). Avec ces lignes, nous pouvons enfermer des zones.
Comment puis-je trouver le plus grand convexe zone noire dans cette image qui ne contient pas de pixel blanc?
Voici un petit exemple dessiné à la main de ce que je veux dire par le plus grand noir convexe Zone:
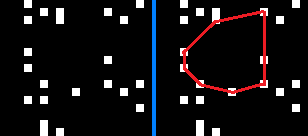
P.S.: l'image n'est pas du bruit, elle représente les nombres premiers inférieurs à 10000000 ordonnés horizontalement.
5 réponses
Je vais esquisser un algorithme de poly-temps correct. Sans aucun doute, il y a des améliorations structurelles des données à apporter, mais je crois qu'une meilleure compréhension de ce problème en particulier sera nécessaire pour rechercher de très grands ensembles de données (ou, peut-être, une limite supérieure ad hoc sur les dimensions de la boîte contenant le polygone).
La boucle principale consiste à deviner le point le plus bas p dans le plus grand polygone convexe (rompre les liens en faveur du point le plus à gauche), puis à calculer le plus grand polygone convexe qui peut être avec p et des points q tels que (Q. Y > P. y) | | (Q. Y = = P. y & & Q. x > P. x).
Le programme dynamique repose sur les mêmes faits géométriques que Le scan de Graham. Supposons sans perte de généralité que p = (0, 0) et trie les points q dans l'ordre de l'angle antihoraire qu'ils font avec l'axe des abscisses (comparez deux points en considérant le signe de leur produit dot). Laissez-les points dans l'ordre de tri être q1, ..., qn. Laissez q0 = p. pour chaque 0 ≤ i 0, un sous-ensemble de q1, ..., qi - 1, q, je, et qj.
Les cas de base où i = 0 sont faciles, puisque le seul "polygone" est le segment de zone zéro q0q j . Par induction, pour calculer le (i, j), nous allons essayer, pour tous 0 ≤ k ≤ i, l'extension de la (k, i) polygone (i, j). Quand pouvons-nous faire cela? En premier lieu, le triangle q0q, jeqj ne doit pas contenir d'autres points. L'autre condition est que l'angle qkq, jeqj vaut mieux ne pas être un virage à droite (encore une fois, vérifiez le signe du produit scalaire).
À la fin, renvoie le plus grand polygone trouvé. Pourquoi ce travail? Il n'est pas difficile de prouver que les polygones convexes ont la sous structure optimale requise par le programme dynamique et que le programme considère exactement ces polygones satisfaisant ceux de Graham la caractérisation de la convexité.
Essayer de trouver la zone convexe maximale est une tâche difficile à faire. Ne seriez-vous pas d'accord pour trouver rectangles avec une surface maximale? Ce problème est beaucoup plus facile et peut être résolu en temps O(N) - linéaire en nombre de pixels. L'algorithme qui suit.
Dites que vous voulez trouver le plus grand rectangle de pixels libres (blancs) (Désolé, j'ai des images avec des couleurs différentes-le blanc est équivalent à votre Noir, Le Gris est équivalent à votre Blanc).
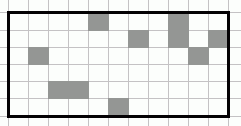
Vous pouvez le faire très efficacement par deux passes linéaire O(n) Temps algorithme (n étant le nombre de pixels):
1) dans un premier passage , passez par colonnes, de bas en haut, et pour chaque pixel, indiquez le nombre de pixels consécutifs disponibles jusqu'à celui-ci:
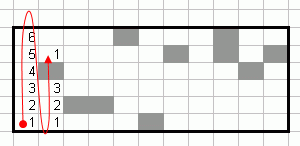
Répéter jusqu'à ce que:
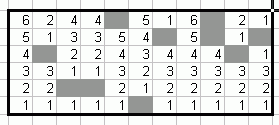
2) dans un deuxième passage , allez par lignes, lisez current_number. Pour chaque nombre k Gardez une trace des sommes de nombres consécutifs qui étaient >= k (c.-à-d. potentiel rectangles de hauteur k). Fermez les sommes (rectangles potentiels) pour k > current_number et regardez si la somme (~zone du rectangle) est supérieure au maximum actuel - si oui, mettez à jour le maximum. À la fin de chaque ligne, fermez tous les rectangles potentiels ouverts (pour tous les k).
De cette façon, vous obtiendrez tous les rectangles maximum. Ce n'est pas la même chose que la zone convexe maximale bien sûr, mais vous donnerait probablement quelques indices (quelques heuristiques) sur l'endroit où chercher des zones convexes maximales.
Vous pouvez essayer de traiter les pixels comme des sommets et d'effectuer la triangulation Delaunay du pointset. Ensuite, vous devez trouver le plus grand ensemble de triangles connectés qui ne crée pas de forme concave et n'a pas de Sommets internes.
Si je comprends bien votre problème, c'est une instance D'étiquetage des composants connectés. Vous pouvez commencer par exemple à: http://en.wikipedia.org/wiki/Connected-component_labeling
J'ai pensé à une approche pour résoudre ce problème:
À partir de l'ensemble de tous les points, générez tous les sous-ensembles possibles de 3 points. C'est un ensemble de tous les triangles dans votre espace. De cet ensemble supprimer tous les triangles qui contiennent un autre point et vous obtenez l'ensemble de tous les triangles vides.
Pour chacun des triangles vides, vous le développeriez à sa taille maximale. C'est-à-dire que pour chaque point en dehors du rectangle, vous l'insérez entre les deux points les plus proches du polygone et Vérifiez s'il y a des points dans ce nouveau triangle. Sinon, vous vous souviendrez de ce point et de la zone qu'il ajoute. Pour chaque nouveau point, vous souhaitez ajouter celui qui maximise la zone ajoutée. Lorsque plus aucun point ne peut être ajouté, le polygone convexe maximum a été construit. Enregistrez la zone pour chaque polygone et souvenez-vous de celle avec la plus grande surface.
Crucial pour la performance de cet algorithme est votre capacité à déterminer a) si un point se trouve dans un triangle et b) si le polygone reste convexe après avoir ajouté un certain point.
Je pense que vous pouvez réduire b) pour être un problème de a) et alors vous avez seulement besoin de trouver la méthode la plus efficace pour déterminer si un point est dans un triangle. La réduction de l'espace de recherche peut être réalisée comme suit: prenez un triangle et augmentez tous les bords à une longueur infinie dans les deux sens. Cela sépare la zone à l'extérieur du triangle en 6 sous-régions. Bon pour nous, c'est que seulement 3 de ces sous-régions peuvent contenir des points respecter la contrainte de convexité. Ainsi, pour chaque point que vous testez, vous devez déterminer si c'est dans une sous-région à expansion convexe, ce qui est encore la question de savoir si c'est dans un certain triangle.
L'ensemble du polygone au fur et à mesure qu'il évolue et s'approche de la forme d'un cercle aura des régions de plus en plus petites qui permettent encore une expansion convexe. Un point une fois dans une région concave ne fera pas partie de la région d'expansion convexe à nouveau de sorte que vous pouvez réduire rapidement le nombre de points que vous aurez avoir à considérer pour l'expansion. En outre, tout en testant des points pour l'expansion, vous pouvez réduire davantage la liste des points possibles. Si un point est testé faux, alors il est dans la sous-région concave d'un autre point et donc tous les autres points dans la sous-région concave des points testés n'ont pas besoin d'être considérés car ils sont également dans la sous-région concave du point intérieur. Vous devriez être en mesure de réduire à une liste de points possibles très rapidement.
Vous devez toujours le faire pour chaque vide triangle bien sûr.
Malheureusement, je ne peux pas garantir qu'en ajoutant toujours la nouvelle région maximale, votre polygone devient le polygone maximum possible.