Imprécision FFT pour C#
ce qui se passe, c'est que j'ai un MIDI (généré à partir de GuitarPro) converti en fichier WAV (44.1 khz, 16-bit, mono) qui contient une progression de pitch à partir de E2 (la note de guitare la plus basse) jusqu'à environ E6. Les résultats pour les notes plus basses (autour de E2-B3) sont généralement très mauvaise. Mais atteindre C4 son quelque peu correcte en ce que vous pouvez déjà voir la progression appropriée (note suivante est C#4, puis D4, etc.) Cependant, le problème est que le pas détecté est une demi-note inférieure au pas réel (par exemple, C4 doit être la note mais D#4 est affiché).
à votre avis, Qu'est-ce qui ne va pas? Je peux poster le code si nécessaire. Merci beaucoup! La GI commence toujours à comprendre le domaine du DSP.
Edit: Voici une ébauche de ce que Im faire
byte[] buffer = new byte[8192];
int bytesRead;
do
{
bytesRead = stream16.Read(buffer, 0, buffer.Length);
} while (bytesRead != 0);
Et ensuite: (waveBuffer est simplement une classe dont le rôle est de convertir le byte[] en float[] étant donné que la fonction accepte uniquement float[])
public int Read(byte[] buffer, int offset, int bytesRead)
{
int frames = bytesRead / sizeof(float);
float pitch = DetectPitch(waveBuffer.FloatBuffer, frames);
}
et enfin: (Smbpitchfft est la classe qui a l'algo FFT ... je crois que theres rien de mal avec elle, donc je ne suis pas le poster ici)
private float DetectPitch(float[] buffer, int inFrames)
{
Func<int, int, float> window = HammingWindow;
if (prevBuffer == null)
{
prevBuffer = new float[inFrames]; //only contains zeroes
}
// double frames since we are combining present and previous buffers
int frames = inFrames * 2;
if (fftBuffer == null)
{
fftBuffer = new float[frames * 2]; // times 2 because it is complex input
}
for (int n = 0; n < frames; n++)
{
if (n < inFrames)
{
fftBuffer[n * 2] = prevBuffer[n] * window(n, frames);
fftBuffer[n * 2 + 1] = 0; // need to clear out as fft modifies buffer
}
else
{
fftBuffer[n * 2] = buffer[n - inFrames] * window(n, frames);
fftBuffer[n * 2 + 1] = 0; // need to clear out as fft modifies buffer
}
}
SmbPitchShift.smbFft(fftBuffer, frames, -1);
}
et pour interpréter le résultat:
float binSize = sampleRate / frames;
int minBin = (int)(82.407 / binSize); //lowest E string on the guitar
int maxBin = (int)(1244.508 / binSize); //highest E string on the guitar
float maxIntensity = 0f;
int maxBinIndex = 0;
for (int bin = minBin; bin <= maxBin; bin++)
{
float real = fftBuffer[bin * 2];
float imaginary = fftBuffer[bin * 2 + 1];
float intensity = real * real + imaginary * imaginary;
if (intensity > maxIntensity)
{
maxIntensity = intensity;
maxBinIndex = bin;
}
}
return binSize * maxBinIndex;
mise à JOUR (si quelqu'un est intéressé (e):
Donc, l'une des réponses ci-dessous elle a déclaré que la crête de fréquence à partir du FFT n'est pas toujours équivalente au pas. Je comprends que. Mais je voulais essayer quelque chose par moi-même si c'était le cas (en partant de l'hypothèse qu'il y a des moments où le pic de fréquence est la hauteur résultante). Donc en gros, j'ai 2 logiciels (SpectraPLUS et FFTProperties de DewResearch ; crédits pour eux) qui sont capables d'afficher le domaine de fréquence pour les signaux audio.
voici donc les résultats des pics de fréquence dans le temps domaine:
SpectraPLUS
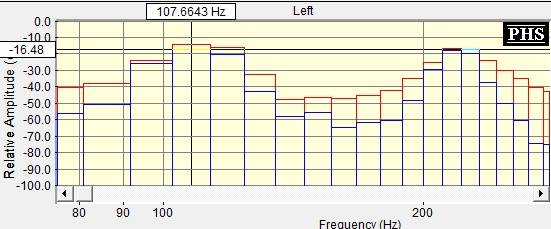
et les propriétés FFT:

ceci a été fait en utilisant une note test de A2 (environ 110Hz). En regardant les images, ils ont des pics de fréquence autour de la gamme de 102-112 Hz pour SpectraPLUS et 108 Hz pour les propriétés FFT. Sur mon code, j'obtiens 104Hz (j'utilise 8192 blocs et un samplerate de 44,1 khz ... 8192 est alors doublé pour le rendre complexe entrée donc à la fin, je obtiens environ 5Hz pour binsize, par rapport à la binsize de 10Hz de SpectraPLUS).
donc maintenant je suis un peu confus, car sur les logiciels ils semblent retourner le bon résultat mais sur mon code, j'ai toujours 104Hz (notez que j'ai comparé la fonction FFT que j'ai utilisée avec d'autres comme Math.Net and it seems to be correct).
pensez-vous que le problème peut être avec mon interprétation des données? Ou les logiciels font-ils autre chose avant d'afficher le spectre de fréquences? Merci!
4 réponses
il semble que vous ayez un problème d'interprétation avec votre sortie FFT. Quelques points aléatoires:
le FFT a une résolution finie - chaque bin de sortie a une résolution de
Fs / N, oùFsest le taux d'échantillonnage etNest la taille du FFTpour les notes qui sont basses sur l'échelle musicale, la différence de fréquence entre les notes successives est relativement faible, donc vous aurez besoin d'un N suffisamment grand pour (voir note 1 au-dessous)
la première série (indice 0) contient l'énergie centrée à 0 Hz mais inclut l'énergie de
+/- Fs / 2Nbin
icontient de l'énergie centrée suri * Fs / Nmais inclut l'énergie de+/- Fs / 2Nchaque côté de cette fréquence centralevous obtiendrez fuite spectrale à partir des bacs adjacents-la gravité de la situation dépend de ce qui fonction de fenêtre vous utilisez-pas de fenêtre (==fenêtre rectangulaire) et la fuite spectrale sera très mauvaise ( très larges pics) - pour l'estimation de fréquence vous voulez choisir une fonction de fenêtre qui vous donne des pics pointus
le pitch n'est pas la même chose que la fréquence-le pitch est un percept, la fréquence est une quantité physique - le pitch perçu d'un instrument de musique peut être légèrement différent de la fréquence fondamentale, selon le type d'instrument (certains instruments ne produisent même pas d'énergie significative à leur fréquence fondamentale, mais nous percevons encore leur hauteur comme si la fondamentale était présente)
Ma meilleure supposition d'après les informations limitées disponibles est que peut-être vous êtes "off by one" quelque part dans votre conversion de bin index en fréquence, ou peut-être votre FFT est trop petit pour vous donner une résolution suffisante pour les notes basses, et vous pourriez avoir besoin d'augmenter N.
vous pouvez aussi améliorez votre estimation de fréquence en utilisant plusieurs techniques, comme l'analyse cepstrale, ou en regardant la composante de phase de votre sortie FFT et en la comparant pour des FFTs successifs (cela permet une estimation de fréquence plus précise à l'intérieur d'une cellule pour une taille de FFT donnée).
Notes
(1) juste pour mettre quelques nombres sur ceci, E2 est 82.4 Hz, F2 est 87.3 Hz, donc vous avez besoin d'une résolution un peu meilleure que 5 Hz pour distinguer entre les deux notes les plus basses sur une guitare (et beaucoup plus fin que cela si vous voulez réellement faire, disons, un accord précis). Pour un échantillon de 44,1 kHz, vous avez probablement besoin d'un FFT D'au moins N = 8192 pour vous donner une résolution suffisante (44100 / 8192 = 5,4 Hz), probablement N = 16384 serait mieux.
j'ai pensé que cela pourrait vous aider. J'ai fait quelques tracés des 6 cordes ouvertes d'une guitare. Le code est en Python en utilisant pylab, que je recommande pour expérimenter:
# analyze distorted guitar notes from
# http://www.freesound.org/packsViewSingle.php?id=643
#
# 329.6 E - open 1st string
# 246.9 B - open 2nd string
# 196.0 G - open 3rd string
# 146.8 D - open 4th string
# 110.0 A - open 5th string
# 82.4 E - open 6th string
from pylab import *
import wave
fs = 44100.0
N = 8192 * 10
t = r_[:N] / fs
f = r_[:N/2+1] * fs / N
gtr_fun = [329.6, 246.9, 196.0, 146.8, 110.0, 82.4]
gtr_wav = [wave.open('dist_gtr_{0}.wav'.format(n),'r') for n in r_[1:7]]
gtr = [fromstring(g.readframes(N), dtype='int16') for g in gtr_wav]
gtr_t = [g / float64(max(abs(g))) for g in gtr]
gtr_f = [2 * abs(rfft(g)) / N for g in gtr_t]
def make_plots():
for n in r_[:len(gtr_t)]:
fig = figure()
fig.subplots_adjust(wspace=0.5, hspace=0.5)
subplot2grid((2,2), (0,0))
plot(t, gtr_t[n]); axis('tight')
title('String ' + str(n+1) + ' Waveform')
subplot2grid((2,2), (0,1))
plot(f, gtr_f[n]); axis('tight')
title('String ' + str(n+1) + ' DFT')
subplot2grid((2,2), (1,0), colspan=2)
M = int(gtr_fun[n] * 16.5 / fs * N)
plot(f[:M], gtr_f[n][:M]); axis('tight')
title('String ' + str(n+1) + ' DFT (16 Harmonics)')
if __name__ == '__main__':
make_plots()
show()
Chaîne 1, fondamentale = 329.6 Hz:
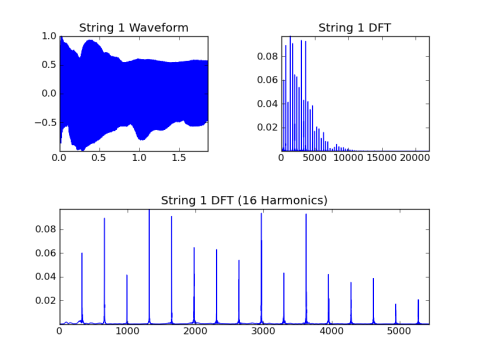
Chaîne 2, fondamentale = 246.9 Hz:

Chaîne 3, fondamentale = 196.0 Hz:
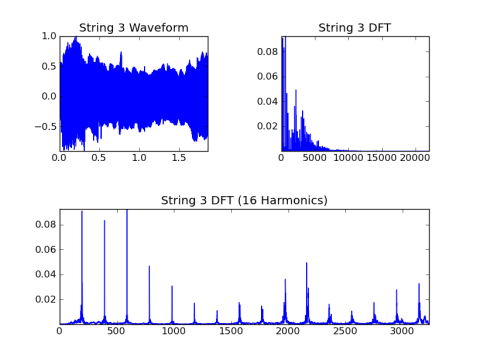
chaîne 4, fondamentale = 146,8 Hz:
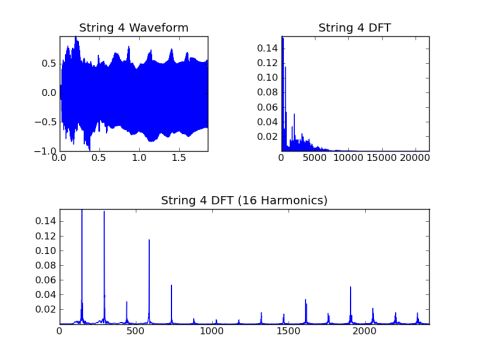
Chaîne 5, fondamentale = 110,0 en Hz:
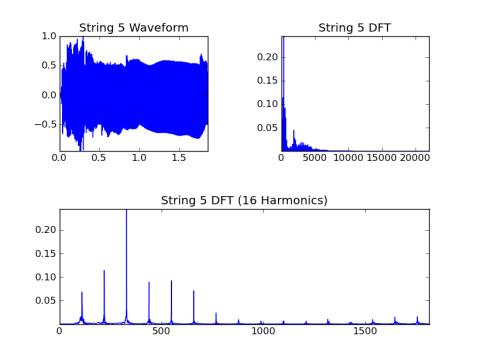
Chaîne 6, fondamentale = 82.4 Hz:
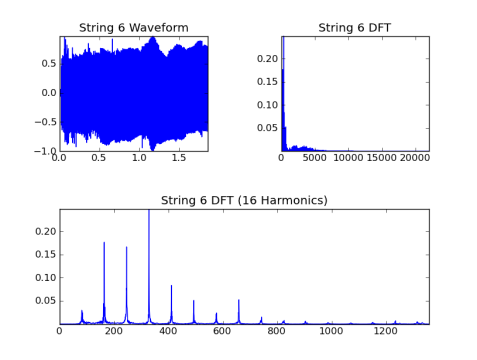
la fréquence fondamentale n'est pas toujours l'harmonique dominant. Il détermine l'espacement entre les harmoniques d'un signal périodique.
j'ai eu un question similaireGoertzel au lieu de la FFT. Si vous savez quels tons vous recherchez (MIDI) Goertzel est capable de détecter les tons à l'intérieur d'une onde sinusale (un cycle). Il le fait en générant l'onde sinusale du son et en le "plaçant au-dessus des données brutes" pour voir s'il existe. FFT prélève de grandes quantités de données pour fournir un spectre de fréquence approximatif.
le pitch Musical est différent du pic de fréquence. Le Pitch est un phénomène Psycho-perceptuel qui peut dépendre davantage des harmoniques et autres. La fréquence de ce qu'un humain appellerait le pitch pourrait être manquante ou très faible dans le spectre du signal réel.
et un pic de fréquence dans un spectre peut être différent de n'importe quel centre de bin FFT. Les fréquences centrales de la binaison FFT changeront de fréquence et d'espacement uniquement en fonction de la longueur de la FFT et de la vitesse d'échantillonnage, et non pas des spectres dans la données.
vous avez donc au moins 2 problèmes à résoudre. Il existe une tonne de documents universitaires sur l'estimation de fréquence ainsi que le sujet distinct de l'estimation de pitch. Commencer par là.