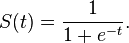Algorithme sigmoïde rapide

Il est préférable de mesurer sur votre matériel en premier. Juste un rapide benchmark script montre, que sur ma machine 1/(1+|x|) est le plus rapide, et tanh(x) est la seconde près. La fonction d'erreur erf est assez rapide aussi.

% gcc -Wall -O2 -lm -o sigmoid-bench{,.c} -std=c99 && ./sigmoid-bench
atan(pi*x/2)*2/pi   24.1 ns
atan(x)             23.0 ns
1/(1+exp(-x))       20.4 ns
1/sqrt(1+x^2)       13.4 ns
erf(sqrt(pi)*x/2)    6.7 ns
tanh(x)              5.5 ns
x/(1+|x|)            5.5 ns

Je m'attends à ce que les résultats puissent varier en fonction de l'architecture et du compilateur utilisé, mais erf(x) (depuis C99), tanh(x) et x/(1.0+fabs(x)) sont susceptibles d'être les plus performants.

Les gens ici sont principalement préoccupés par la vitesse à laquelle une fonction est relative à une autre et créent des micro benchmark pour voir si f1(x) exécute 0,0001 ms plus rapidement que f2(x). Le gros problème est que ce n'est surtout pas pertinent, car ce qui importe, c'est la vitesse à laquelle votre réseau apprend avec votre fonction d'activation en essayant de minimiser votre fonction de coût.

Comme de la théorie actuelle, redresseur de fonction et softplus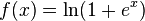

Par rapport à la fonction sigmoïde ou similaire fonctions d'activation, permettre pour une formation plus rapide et efficace des architectures neuronales profondes sur ensembles de données volumineux et complexes.

Je suggère donc de jeter la micro-optimisation, et de jeter un oeil à quelle fonction permet un apprentissage plus rapide (en regardant également diverses autres fonctions de coût).

Pour faire le NN plus flexible habituellement utilisé un taux alpha pour changer l'angle du graphique autour de 0.

La fonction sigmoïde ressemble à:

f(x) = 1 / ( 1+exp(-x*alpha))

La fonction presque équivalente, (mais plus rapide) est:

f(x) = 0.5 * (x * alpha / (1 + abs(x*alpha))) + 0.5

Vous pouvez vérifier les graphes ici

Lorsque j'utilise la fonction abs, le réseau devient plus rapide 100 fois.

Cette réponse n'est probablement pas pertinente pour la plupart des cas, mais je voulais juste dire que pour CUDA computing, j'ai trouvé x/sqrt(1+x^2) la fonction la plus rapide de loin.

Par exemple, fait avec des intrinsèques flottantes de précision unique:

__device__ void fooCudaKernel(/* some arguments */) {
    float foo, sigmoid;
    // some code defining foo
    sigmoid = __fmul_rz(rsqrtf(__fmaf_rz(foo,foo,1)),foo);
}

Vous pouvez également utiliser une version approximative de sigmoid (elle ne diffère pas de 0,2% de l'original):

    inline float RoughSigmoid(float value)
    {
        float x = ::abs(value);
        float x2 = x*x;
        float e = 1.0f + x + x2*0.555f + x2*x2*0.143f;
        return 1.0f / (1.0f + (value > 0 ? 1.0f / e : e));
    }

    void RoughSigmoid(const float * src, size_t size, const float * slope, float * dst)
    {
        float s = slope[0];
        for (size_t i = 0; i < size; ++i)
            dst[i] = RoughSigmoid(src[i] * s);
    }

Optimisation de la fonction RoughSigmoid avec L'utilisation de SSE:

    #include <xmmintrin.h>

    void RoughSigmoid(const float * src, size_t size, const float * slope, float * dst)
    {
        size_t alignedSize =  size/4*4;
        __m128 _slope = _mm_set1_ps(*slope);
        __m128 _0 = _mm_set1_ps(-0.0f);
        __m128 _1 = _mm_set1_ps(1.0f);
        __m128 _0555 = _mm_set1_ps(0.555f);
        __m128 _0143 = _mm_set1_ps(0.143f);
        size_t i = 0;
        for (; i < alignedSize; i += 4)
        {
            __m128 _src = _mm_loadu_ps(src + i);
            __m128 x = _mm_andnot_ps(_0, _mm_mul_ps(_src, _slope));
            __m128 x2 = _mm_mul_ps(x, x);
            __m128 x4 = _mm_mul_ps(x2, x2);
            __m128 series = _mm_add_ps(_mm_add_ps(_1, x), _mm_add_ps(_mm_mul_ps(x2, _0555), _mm_mul_ps(x4, _0143)));
            __m128 mask = _mm_cmpgt_ps(_src, _0);
            __m128 exp = _mm_or_ps(_mm_and_ps(_mm_rcp_ps(series), mask), _mm_andnot_ps(mask, series));
            __m128 sigmoid = _mm_rcp_ps(_mm_add_ps(_1, exp));
            _mm_storeu_ps(dst + i, sigmoid);
        }
        for (; i < size; ++i)
            dst[i] = RoughSigmoid(src[i] * slope[0]);
    }

Optimisation de la fonction RoughSigmoid avec L'utilisation de AVX:

    #include <immintrin.h>

    void RoughSigmoid(const float * src, size_t size, const float * slope, float * dst)
    {
        size_t alignedSize = size/8*8;
        __m256 _slope = _mm256_set1_ps(*slope);
        __m256 _0 = _mm256_set1_ps(-0.0f);
        __m256 _1 = _mm256_set1_ps(1.0f);
        __m256 _0555 = _mm256_set1_ps(0.555f);
        __m256 _0143 = _mm256_set1_ps(0.143f);
        size_t i = 0;
        for (; i < alignedSize; i += 8)
        {
            __m256 _src = _mm256_loadu_ps(src + i);
            __m256 x = _mm256_andnot_ps(_0, _mm256_mul_ps(_src, _slope));
            __m256 x2 = _mm256_mul_ps(x, x);
            __m256 x4 = _mm256_mul_ps(x2, x2);
            __m256 series = _mm256_add_ps(_mm256_add_ps(_1, x), _mm256_add_ps(_mm256_mul_ps(x2, _0555), _mm256_mul_ps(x4, _0143)));
            __m256 mask = _mm256_cmp_ps(_src, _0, _CMP_GT_OS);
            __m256 exp = _mm256_or_ps(_mm256_and_ps(_mm256_rcp_ps(series), mask), _mm256_andnot_ps(mask, series));
            __m256 sigmoid = _mm256_rcp_ps(_mm256_add_ps(_1, exp));
            _mm256_storeu_ps(dst + i, sigmoid);
        }
        for (; i < size; ++i)
            dst[i] = RoughSigmoid(src[i] * slope[0]);
    }

Vous pouvez utiliser une méthode simple mais efficace en utilisant deux formules:

if x < 0 then f(x) = 1 / (0.5/(1+(x^2)))
if x > 0 then f(x) = 1 / (-0.5/(1+(x^2)))+1

Cela ressemblera à ceci:

Deux graphiques pour une sigmoïde {en Bleu: (0.5/(1+(x^2))), Jaune: (-0.5/(1+(x^2)))+1}

En utilisant Eureqa pour rechercher des approximations à sigmoïde j'ai trouvé 1/(1 + 0.3678749025^x) l'approximation. C'est assez proche, juste se débarrasse d'une opération avec la négation de X.

Certaines des autres fonctions présentées ici sont intéressantes, mais l'opération d'alimentation est-elle vraiment si lente? Je l'ai testé et il a fait plus vite que l'addition, mais cela pourrait juste être un coup de chance. Si c'est le cas, il devrait être aussi rapide ou plus rapide que tous les autres.

EDIT:0.5 + 0.5*tanh(0.5*x) et moins précis, 0.5 + 0.5*tanh(n) fonctionne également. Et vous pourriez débarrassez-vous simplement des constantes si vous ne vous souciez pas de l'obtenir entre la plage [0,1] comme sigmoid. Mais il suppose que tanh est plus rapide.

La fonction tanh peut être optimisée dans certaines langues, ce qui la rend plus rapide qu'un X/(1+abs(x)) défini sur mesure, tel est le cas dans Julia.

Je ne pense pas que vous puissiez faire mieux que l'exp() intégré, mais si vous voulez une autre approche, vous pouvez utiliser l'expansion de la série. WolframAlpha peut le calculer pour vous.