Interpolation linéaire rapide en Num Py /Scipy " le long d'un chemin"
disons que j'ai des données de stations météorologiques à 3 (connu) altitude sur une montagne. Plus précisément, chaque station enregistre une mesure de la température à son emplacement chaque minute. J'ai deux types d'interpolation j'aimerais effectuer. Et je voudrais être en mesure d'exécuter chaque rapidement.
Donc, nous allons définir quelques données:
import numpy as np
from scipy.interpolate import interp1d
import pandas as pd
import seaborn as sns
np.random.seed(0)
N, sigma = 1000., 5
basetemps = 70 + (np.random.randn(N) * sigma)
midtemps = 50 + (np.random.randn(N) * sigma)
toptemps = 40 + (np.random.randn(N) * sigma)
alltemps = np.array([basetemps, midtemps, toptemps]).T # note transpose!
trend = np.sin(4 / N * np.arange(N)) * 30
trend = trend[:, np.newaxis]
altitudes = np.array([500, 1500, 4000]).astype(float)
finaltemps = pd.DataFrame(alltemps + trend, columns=altitudes)
finaltemps.index.names, finaltemps.columns.names = ['Time'], ['Altitude']
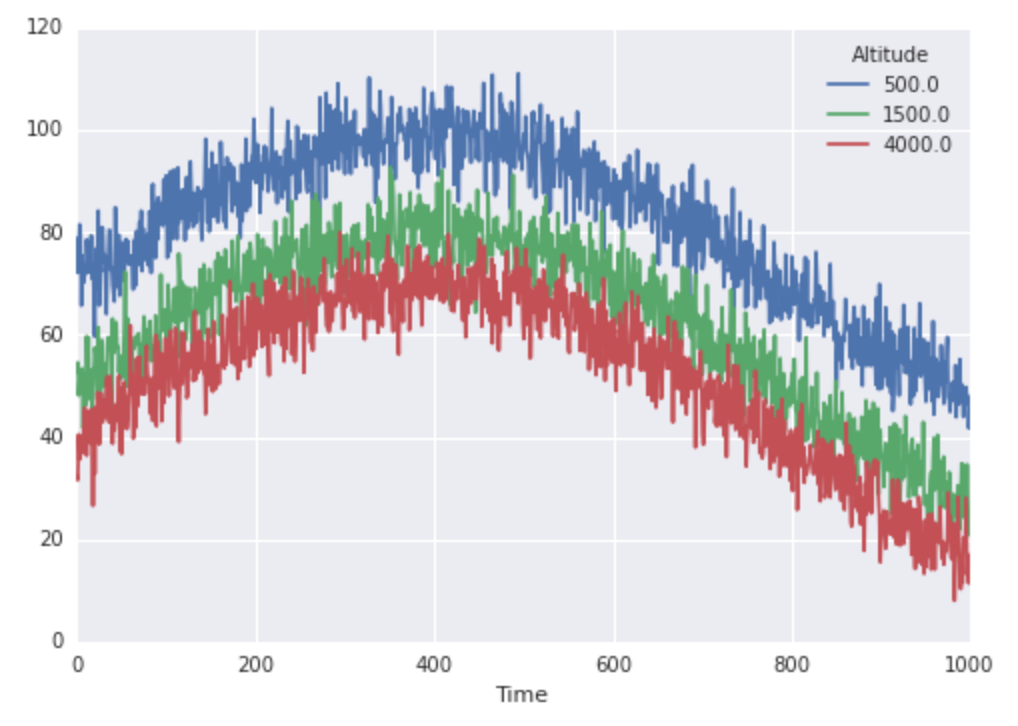
finaltemps.plot()
Super, donc nos températures ressemblent à ceci:
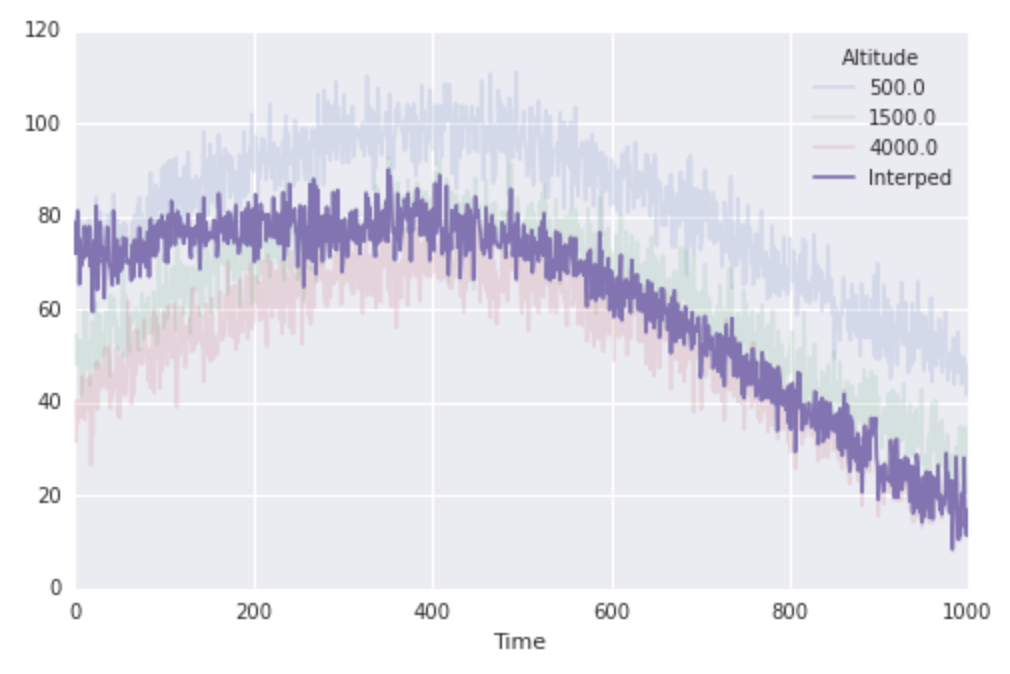
interpoler tout le temps pour la même altitude:
je pense que c'est assez simple. Disons que je veux obtenir la température à une altitude de 1000 pour chaque fois. Je peux juste utiliser construite en scipy méthodes d'interpolation:
interping_function = interp1d(altitudes, finaltemps.values)
interped_to_1000 = interping_function(1000)
fig, ax = plt.subplots(1, 1, figsize=(8, 5))
finaltemps.plot(ax=ax, alpha=0.15)
ax.plot(interped_to_1000, label='Interped')
ax.legend(loc='best', title=finaltemps.columns.name)
cela fonctionne bien. Et nous allons voir à propos de la vitesse:
%%timeit
res = interp1d(altitudes, finaltemps.values)(1000)
#-> 1000 loops, best of 3: 207 µs per loop
Interpoler "le long d'un chemin":
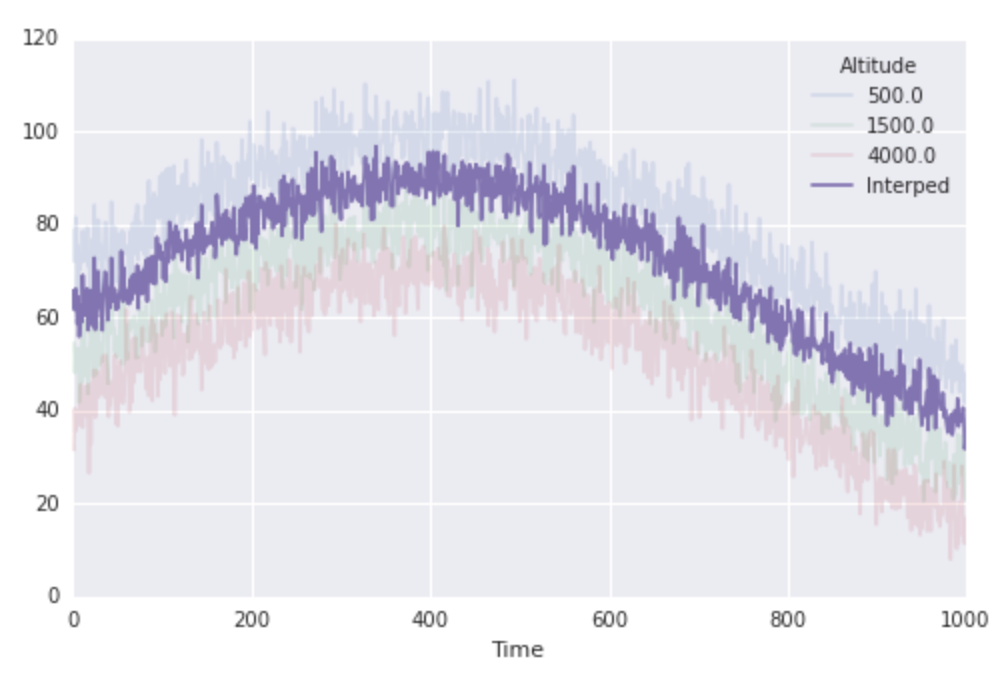
alors maintenant j'ai un second problème, relié. Dire que je connais l'altitude d'une randonnée partie en fonction du temps, et je veux calculer la température à leur (déménagement) emplacement par interpolation linéaire mes données à travers le temps. en particulier, les moments où je connais l'emplacement de la partie de randonnée sont les fois où je connais les températures à mes stations météorologiques. je peux le faire sans trop d'effort:
location = np.linspace(altitudes[0], altitudes[-1], N)
interped_along_path = np.array([interp1d(altitudes, finaltemps.values[i, :])(loc)
for i, loc in enumerate(location)])
fig, ax = plt.subplots(1, 1, figsize=(8, 5))
finaltemps.plot(ax=ax, alpha=0.15)
ax.plot(interped_along_path, label='Interped')
ax.legend(loc='best', title=finaltemps.columns.name)
donc ça marche très bien, mais c'est important pour noter que la ligne clé ci-dessus utilise la compréhension de liste pour cacher une énorme quantité de travail. Dans le cas précédent, scipy crée une seule fonction d'interpolation pour nous, et l'évalue une fois sur une grande quantité de données. Dans ce cas, scipy est en train de construire N fonctions d'interpolation individuelles et évaluation de chacune une fois sur une petite quantité de données. Cela semble intrinsèquement inefficace. Il y a une boucle for qui se cache ici (dans la liste de compréhension) et d'ailleurs, ce juste se sent molle.
il N'est pas surprenant que ce soit beaucoup plus lent que le cas précédent:
%%timeit
res = np.array([interp1d(altitudes, finaltemps.values[i, :])(loc)
for i, loc in enumerate(location)])
#-> 10 loops, best of 3: 145 ms per loop
ainsi le second exemple court 1.000 plus lentement que le premier. I. e. en accord avec l'idée que le levage lourd est le "faire une interpolation linéaire de la fonction"...ce qui se produit 1 000 fois dans le deuxième exemple, mais seulement une fois dans le premier.
alors, la question:est-il une meilleure façon d'aborder le deuxième problème? Par exemple, est-il une bonne façon de le mettre en place avec une interpolation tridimensionnelle (qui pourrait peut-être gérer le cas où les moments où les emplacements de la partie de randonnée sont connus sont les moments où les températures ont été échantillonnées)? Ou y a-t-il une façon particulièrement habile de gérer les choses ici où les temps s'alignent? Ou d'autres?
3 réponses
pour un point fixe dans le temps, vous pouvez utiliser la fonction d'interpolation suivante:
g(a) = cc[0]*abs(a-aa[0]) + cc[1]*abs(a-aa[1]) + cc[2]*abs(a-aa[2])
où a est l'altitude du randonneur,aa vecteur avec les 3 mesure altitudes et cc est un vecteur avec les coefficients. Il y a trois choses à noter:
- pour des températures données (
alltemps) correspondant àaa, la détermination deccpeut être fait en résolvant une équation de matrice linéaire en utilisantnp.linalg.solve(). g(a)est facile à vectoriser pour un (N,) dimensionsaet (N, 3) dimensionnelcc(np.linalg.solve()respectivement).g(a)est appelé un noyau à une variable de premier ordre (pour trois points). En utilisantabs(a-aa[i])**(2*d-1)changerait l'ordre de spline end. Cette approche pourrait être interprétée d'une version simplifiée d'un Processus Gaussien dans l'Apprentissage de la Machine.
Donc le code:
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
# generate temperatures
np.random.seed(0)
N, sigma = 1000, 5
trend = np.sin(4 / N * np.arange(N)) * 30
alltemps = np.array([tmp0 + trend + sigma*np.random.randn(N)
for tmp0 in [70, 50, 40]])
# generate attitudes:
altitudes = np.array([500, 1500, 4000]).astype(float)
location = np.linspace(altitudes[0], altitudes[-1], N)
def doit():
""" do the interpolation, improved version for speed """
AA = np.vstack([np.abs(altitudes-a_i) for a_i in altitudes])
# This is slighty faster than np.linalg.solve(), because AA is small:
cc = np.dot(np.linalg.inv(AA), alltemps)
return (cc[0]*np.abs(location-altitudes[0]) +
cc[1]*np.abs(location-altitudes[1]) +
cc[2]*np.abs(location-altitudes[2]))
t_loc = doit() # call interpolator
# do the plotting:
fg, ax = plt.subplots(num=1)
for alt, t in zip(altitudes, alltemps):
ax.plot(t, label="%d feet" % alt, alpha=.5)
ax.plot(t_loc, label="Interpolation")
ax.legend(loc="best", title="Altitude:")
ax.set_xlabel("Time")
ax.set_ylabel("Temperature")
fg.canvas.draw()
Mesurer le temps donne:
In [2]: %timeit doit()
10000 loops, best of 3: 107 µs per loop
mise à Jour: j'ai remplacé l'original interprétations de la liste doit()
importer la vitesse de 30% (pour N=1000).
10 loops, best of 3: 110 ms per loop
interp_checked
10000 loops, best of 3: 83.9 µs per loop
scipy_interpn
1000 loops, best of 3: 678 µs per loop
Output allclose:
[True, True, True]
Notez que N=1000 est un nombre relativement petit. En utilisant N=100000 produit les résultats:
interp_checked
100 loops, best of 3: 8.37 ms per loop
%timeit doit()
100 loops, best of 3: 5.31 ms per loop
cela montre que cette approche est mieux adaptée aux grands N que le interp_checked approche.
Une interpolation linéaire entre deux valeurs y1,y2 à des endroits x1 et x2, en ce qui concerne le point xi est tout simplement:
yi = y1 + (y2-y1) * (xi-x1) / (x2-x1)
avec quelques expressions num Py vectorisées nous pouvons sélectionner les points pertinents de l'ensemble de données et appliquer la fonction ci-dessus:
I = np.searchsorted(altitudes, location)
x1 = altitudes[I-1]
x2 = altitudes[I]
time = np.arange(len(alltemps))
y1 = alltemps[time,I-1]
y2 = alltemps[time,I]
xI = location
yI = y1 + (y2-y1) * (xI-x1) / (x2-x1)
le problème est que certains points se situent sur les limites de (ou même en dehors de) la portée connue, qui devrait être prise en compte:
I = np.searchsorted(altitudes, location)
same = (location == altitudes.take(I, mode='clip'))
out_of_range = ~same & ((I == 0) | (I == altitudes.size))
I[out_of_range] = 1 # Prevent index-errors
x1 = altitudes[I-1]
x2 = altitudes[I]
time = np.arange(len(alltemps))
y1 = alltemps[time,I-1]
y2 = alltemps[time,I]
xI = location
yI = y1 + (y2-y1) * (xI-x1) / (x2-x1)
yI[out_of_range] = np.nan
Heureusement, Scipy fournit déjà l'interpolation ND, qui s'occupe aussi facilement des temps de décalage, par exemple:
from scipy.interpolate import interpn
time = np.arange(len(alltemps))
M = 150
hiketime = np.linspace(time[0], time[-1], M)
location = np.linspace(altitudes[0], altitudes[-1], M)
xI = np.column_stack((hiketime, location))
yI = interpn((time, altitudes), alltemps, xI)
Voici un code de référence (sans pandas en fait, peu, j'ai fait notamment de la solution de l'autre):
import numpy as np
from scipy.interpolate import interp1d, interpn
def original():
return np.array([interp1d(altitudes, alltemps[i, :])(loc)
for i, loc in enumerate(location)])
def OP_self_answer():
return np.diagonal(interp1d(altitudes, alltemps)(location))
def interp_checked():
I = np.searchsorted(altitudes, location)
same = (location == altitudes.take(I, mode='clip'))
out_of_range = ~same & ((I == 0) | (I == altitudes.size))
I[out_of_range] = 1 # Prevent index-errors
x1 = altitudes[I-1]
x2 = altitudes[I]
time = np.arange(len(alltemps))
y1 = alltemps[time,I-1]
y2 = alltemps[time,I]
xI = location
yI = y1 + (y2-y1) * (xI-x1) / (x2-x1)
yI[out_of_range] = np.nan
return yI
def scipy_interpn():
time = np.arange(len(alltemps))
xI = np.column_stack((time, location))
yI = interpn((time, altitudes), alltemps, xI)
return yI
N, sigma = 1000., 5
basetemps = 70 + (np.random.randn(N) * sigma)
midtemps = 50 + (np.random.randn(N) * sigma)
toptemps = 40 + (np.random.randn(N) * sigma)
trend = np.sin(4 / N * np.arange(N)) * 30
trend = trend[:, np.newaxis]
alltemps = np.array([basetemps, midtemps, toptemps]).T + trend
altitudes = np.array([500, 1500, 4000], dtype=float)
location = np.linspace(altitudes[0], altitudes[-1], N)
funcs = [original, interp_checked, scipy_interpn]
for func in funcs:
print(func.func_name)
%timeit func()
from itertools import combinations
outs = [func() for func in funcs]
print('Output allclose:')
print([np.allclose(out1, out2) for out1, out2 in combinations(outs, 2)])
Avec le résultat suivant sur mon système:
original
10 loops, best of 3: 184 ms per loop
OP_self_answer
10 loops, best of 3: 89.3 ms per loop
interp_checked
1000 loops, best of 3: 224 µs per loop
scipy_interpn
1000 loops, best of 3: 1.36 ms per loop
Output allclose:
[True, True, True, True, True, True]
Scipy est interpn souffre un peu en termes de vitesse par rapport à la méthode la plus rapide, mais pour sa généralité et sa facilité de il est certainement le chemin à parcourir.
je vais proposer un peu de progrès. Dans le second cas (interpolation "le long d'un chemin"), nous faisons beaucoup de différentes fonctions d'interpolation. Une chose que nous pourrions essayer est de faire juste une fonction d'interpolation (une qui fait interpolation dans la dimension d'altitude sur tous les temps comme dans le premier cas ci-dessus) et d'évaluer cette fonction encore et encore (d'une manière vectorisée). Cela nous donnerait beaucoup plus de données que nous ne le voulons (cela nous donnerait une matrice de 1 000 x 1 000 au lieu d'une matrice de 1 000 éléments). vecteur.) Mais alors notre résultat cible serait juste le long de la diagonale. Donc, la question Est, est-ce que l'appel d'une seule fonction sur un chemin d'arguments plus complexes s'exécute plus rapidement que de faire de nombreuses fonctions et de les appeler avec des arguments simples?
La réponse est oui!
la clé est que la fonction d'interpolation retourne par scipy.interpolate.interp1d est capable d'accepter un numpy.ndarray comme entrée. Ainsi, vous pouvez effectivement appeler la fonction d'interpolation plusieurs fois à la vitesse C en vous alimentant dans une entrée vectorielle. C'est-à-dire: c'est beaucoup plus rapide que d'écrire une boucle for qui appelle la fonction interpolation encore et encore sur une entrée scalaire. Alors que nous calculons beaucoup de points de données que nous finissons par jeter, nous gagnons encore plus de temps en ne construisant pas beaucoup de différentes fonctions d'interpolation que nous utilisons à peine.
old_way = interped_along_path = np.array([interp1d(altitudes, finaltemps.values[i, :])(loc)
for i, loc in enumerate(location)])
# look ma, no for loops!
new_way = np.diagonal(interp1d(altitudes, finaltemps.values)(location))
# note, `location` is a vector!
abs(old_way - new_way).max()
#-> 0.0
et encore:
%%timeit
res = np.diagonal(interp1d(altitudes, finaltemps.values)(location))
#-> 100 loops, best of 3: 16.7 ms per loop
donc cette approche nous donne un facteur de 10 de mieux! Quelqu'un peut-il faire mieux? Ou suggérer une approche totalement différente?