Exp calcul rapide: possible d'améliorer la précision sans perdre trop de performance?
J'essaie la fonction EXP (x) rapide qui a été décrite précédemment dans cette réponse à une question SO sur l'amélioration de la vitesse de calcul en C#:
public static double Exp(double x)
{
var tmp = (long)(1512775 * x + 1072632447);
return BitConverter.Int64BitsToDouble(tmp << 32);
}
L'expression utilise des "astuces" en virgule flottante IEEE et est principalement destinée à être utilisée dans des ensembles neuronaux. La fonction est environ 5 fois plus rapide que la fonction normale Math.Exp(x).
Malheureusement, la précision numérique n'est que de -4% -- + 2% par rapport à la fonction Math.Exp(x) régulière, idéalement je voudrais avoir une précision dans au moins la plage de sous-pourcentage.
J'ai tracé le quotient entre les fonctions approximatives et les fonctions EXP régulières, et comme on peut le voir sur le graphique, la différence relative semble être répétée avec une fréquence pratiquement constante.
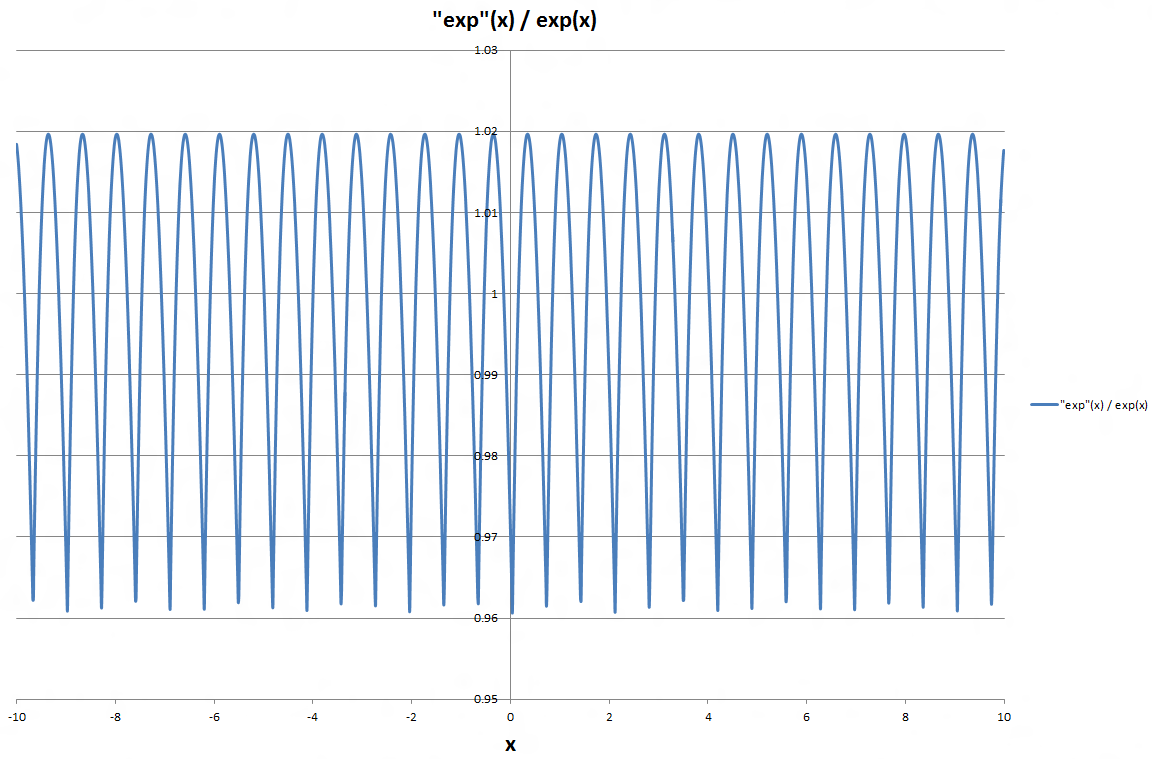
Est-il possible de profiter de cette régularité pour améliorer encore la précision de la fonction "exp rapide" sans réduire sensiblement la vitesse de calcul, ou serait-ce la surcharge de calcul de une amélioration de la précision l'emporte sur le gain de calcul de l'expression originale?
(en note de côté, j'ai également essayé l'une des approches alternatives proposées dans la même question SO, mais cette approche ne semble pas être efficace en C#, du moins pas pour le cas général.)
MISE À JOUR LE 14 MAI
À la demande de @ Adriano, j'ai maintenant effectué un benchmark très simple. J'ai effectué 10 millions de calculs en utilisant chacun des fonctions alternatives exp pour les valeurs à virgule flottante dans la plage [-100, 100]. Puisque la plage de valeurs qui m'intéresse s'étend de -20 à 0, j'ai également explicitement énuméré la valeur de la fonction à x = -5. Voici les résultats:
Math.Exp: 62.525 ms, exp(-5) = 0.00673794699908547
Empty function: 13.769 ms
ExpNeural: 14.867 ms, exp(-5) = 0.00675211846828461
ExpSeries8: 15.121 ms, exp(-5) = 0.00641270968867667
ExpSeries16: 32.046 ms, exp(-5) = 0.00673666189488182
exp1: 15.062 ms, exp(-5) = -12.3333325982094
exp2: 15.090 ms, exp(-5) = 13.708332516253
exp3: 16.251 ms, exp(-5) = -12.3333325982094
exp4: 17.924 ms, exp(-5) = 728.368055056781
exp5: 20.972 ms, exp(-5) = -6.13293614238501
exp6: 24.212 ms, exp(-5) = 3.55518353166184
exp7: 29.092 ms, exp(-5) = -1.8271053775984
exp7 +/-: 38.482 ms, exp(-5) = 0.00695945286970704
ExpNeural est équivalent à la Exp fonction spécifiée dans le début de ce texte. ExpSeries8 est la formulation {[7] } que j'ai initialement revendiquée n'était pas très efficace sur. NET; lors de son implémentation exactement comme Neil il était en fait très rapide. ExpSeries16 est la formule analogue mais avec 16 multiplications au lieu de 8. exp1 à exp7 sont les différentes fonctions de la réponse D'Adriano ci-dessous. La variante finale de exp7 est une variante où le signe de x est vérifié; si négatif, la fonction renvoie 1/exp(-x) à la place.
Malheureusement, aucune des fonctions expN listées par Adriano ne sont suffisantes dans le gamme de valeur négative plus large que je considère. L'approche d'expansion de la série par Neil Coffey semble être plus appropriée dans " ma " plage de valeurs, bien qu'elle soit trop rapidement divergente avec un plus grand négatif x , en particulier lorsque vous utilisez "seulement" 8 multiplications.
5 réponses
Si quelqu'un veut répliquer la fonction d'erreur relative indiquée dans la question, voici un moyen d'utiliser Matlab (L'exposant "rapide" n'est pas très rapide dans Matlab, mais il est précis):
t = 1072632447+[0:ceil(1512775*pi)];
x = (t - 1072632447)/1512775;
ex = exp(x);
t = uint64(t);
import java.lang.Double;
et = arrayfun( @(n) java.lang.Double.longBitsToDouble(bitshift(n,32)), t );
plot(x, et./ex);
Maintenant, la période de l'erreur exactement coïncide avec le moment où la valeur binaire de tmp déborde de la mantisse en l'exposant. Divisons nos données en bins en rejetant les bits qui deviennent l'exposant (en le rendant périodique), et en ne gardant que les huit bits restants (pour rendre notre table de recherche d'une taille raisonnable):
index = bitshift(bitand(t,uint64(2^20-2^12)),-12) + 1;
Maintenant, nous calculons l'ajustement moyen requis:
relerrfix = ex./et;
adjust = NaN(1,256);
for i=1:256; adjust(i) = mean(relerrfix(index == i)); end;
et2 = et .* adjust(index);
L'erreur relative est réduite à +/- .0006. Bien sûr, d'autres tailles de tables sont également possibles (par exemple, une table 6 bits avec 64 entrées donne+/ -.0025) et l'erreur est presque linéaire dans la taille de la table. L'interpolation linéaire entre les entrées de la table améliorerait encore l'erreur, mais au détriment des performances. Puisque nous avons déjà atteint l'objectif de précision, évitons tout outre les performances.
À ce stade, il s'agit de compétences d'éditeur triviales pour prendre les valeurs calculées par MatLab et créer une table de recherche en C#. Pour chaque calcul, nous ajoutons un masque de bits, une recherche de table et une multiplication à double précision.
static double FastExp(double x)
{
var tmp = (long)(1512775 * x + 1072632447);
int index = (int)(tmp >> 12) & 0xFF;
return BitConverter.Int64BitsToDouble(tmp << 32) * ExpAdjustment[index];
}
L'accélération est très similaire au code original-pour mon ordinateur, c'est environ 30% plus rapide compilé en x86 et environ 3 fois plus rapide pour x64. Avec mono sur ideone, c'est une perte nette substantielle (mais c'est aussi le original).
Le code source Complet et cas de test: http://ideone.com/UwNgx
using System;
using System.Diagnostics;
namespace fastexponent
{
class Program
{
static double[] ExpAdjustment = new double[256] {
1.040389835,
1.039159306,
1.037945888,
1.036749401,
1.035569671,
1.034406528,
1.033259801,
1.032129324,
1.031014933,
1.029916467,
1.028833767,
1.027766676,
1.02671504,
1.025678708,
1.02465753,
1.023651359,
1.022660049,
1.021683458,
1.020721446,
1.019773873,
1.018840604,
1.017921503,
1.017016438,
1.016125279,
1.015247897,
1.014384165,
1.013533958,
1.012697153,
1.011873629,
1.011063266,
1.010265947,
1.009481555,
1.008709975,
1.007951096,
1.007204805,
1.006470993,
1.005749552,
1.005040376,
1.004343358,
1.003658397,
1.002985389,
1.002324233,
1.001674831,
1.001037085,
1.000410897,
0.999796173,
0.999192819,
0.998600742,
0.998019851,
0.997450055,
0.996891266,
0.996343396,
0.995806358,
0.995280068,
0.99476444,
0.994259393,
0.993764844,
0.993280711,
0.992806917,
0.992343381,
0.991890026,
0.991446776,
0.991013555,
0.990590289,
0.990176903,
0.989773325,
0.989379484,
0.988995309,
0.988620729,
0.988255677,
0.987900083,
0.987553882,
0.987217006,
0.98688939,
0.98657097,
0.986261682,
0.985961463,
0.985670251,
0.985387985,
0.985114604,
0.984850048,
0.984594259,
0.984347178,
0.984108748,
0.983878911,
0.983657613,
0.983444797,
0.983240409,
0.983044394,
0.982856701,
0.982677276,
0.982506066,
0.982343022,
0.982188091,
0.982041225,
0.981902373,
0.981771487,
0.981648519,
0.981533421,
0.981426146,
0.981326648,
0.98123488,
0.981150798,
0.981074356,
0.981005511,
0.980944219,
0.980890437,
0.980844122,
0.980805232,
0.980773726,
0.980749562,
0.9807327,
0.9807231,
0.980720722,
0.980725528,
0.980737478,
0.980756534,
0.98078266,
0.980815817,
0.980855968,
0.980903079,
0.980955475,
0.981017942,
0.981085714,
0.981160303,
0.981241675,
0.981329796,
0.981424634,
0.981526154,
0.981634325,
0.981749114,
0.981870489,
0.981998419,
0.982132873,
0.98227382,
0.982421229,
0.982575072,
0.982735318,
0.982901937,
0.983074902,
0.983254183,
0.983439752,
0.983631582,
0.983829644,
0.984033912,
0.984244358,
0.984460956,
0.984683681,
0.984912505,
0.985147403,
0.985388349,
0.98563532,
0.98588829,
0.986147234,
0.986412128,
0.986682949,
0.986959673,
0.987242277,
0.987530737,
0.987825031,
0.988125136,
0.98843103,
0.988742691,
0.989060098,
0.989383229,
0.989712063,
0.990046579,
0.990386756,
0.990732574,
0.991084012,
0.991441052,
0.991803672,
0.992171854,
0.992545578,
0.992924825,
0.993309578,
0.993699816,
0.994095522,
0.994496677,
0.994903265,
0.995315266,
0.995732665,
0.996155442,
0.996583582,
0.997017068,
0.997455883,
0.99790001,
0.998349434,
0.998804138,
0.999264107,
0.999729325,
1.000199776,
1.000675446,
1.001156319,
1.001642381,
1.002133617,
1.002630011,
1.003131551,
1.003638222,
1.00415001,
1.004666901,
1.005188881,
1.005715938,
1.006248058,
1.006785227,
1.007327434,
1.007874665,
1.008426907,
1.008984149,
1.009546377,
1.010113581,
1.010685747,
1.011262865,
1.011844922,
1.012431907,
1.013023808,
1.013620615,
1.014222317,
1.014828902,
1.01544036,
1.016056681,
1.016677853,
1.017303866,
1.017934711,
1.018570378,
1.019210855,
1.019856135,
1.020506206,
1.02116106,
1.021820687,
1.022485078,
1.023154224,
1.023828116,
1.024506745,
1.025190103,
1.02587818,
1.026570969,
1.027268461,
1.027970647,
1.02867752,
1.029389072,
1.030114973,
1.030826088,
1.03155163,
1.032281819,
1.03301665,
1.033756114,
1.034500204,
1.035248913,
1.036002235,
1.036760162,
1.037522688,
1.038289806,
1.039061509,
1.039837792,
1.040618648
};
static double FastExp(double x)
{
var tmp = (long)(1512775 * x + 1072632447);
int index = (int)(tmp >> 12) & 0xFF;
return BitConverter.Int64BitsToDouble(tmp << 32) * ExpAdjustment[index];
}
static void Main(string[] args)
{
double[] x = new double[1000000];
double[] ex = new double[x.Length];
double[] fx = new double[x.Length];
Random r = new Random();
for (int i = 0; i < x.Length; ++i)
x[i] = r.NextDouble() * 40;
Stopwatch sw = new Stopwatch();
sw.Start();
for (int j = 0; j < x.Length; ++j)
ex[j] = Math.Exp(x[j]);
sw.Stop();
double builtin = sw.Elapsed.TotalMilliseconds;
sw.Reset();
sw.Start();
for (int k = 0; k < x.Length; ++k)
fx[k] = FastExp(x[k]);
sw.Stop();
double custom = sw.Elapsed.TotalMilliseconds;
double min = 1, max = 1;
for (int m = 0; m < x.Length; ++m) {
double ratio = fx[m] / ex[m];
if (min > ratio) min = ratio;
if (max < ratio) max = ratio;
}
Console.WriteLine("minimum ratio = " + min.ToString() + ", maximum ratio = " + max.ToString() + ", speedup = " + (builtin / custom).ToString());
}
}
}
Essayez les solutions suivantes (exp1 est plus rapide, exp7 est plus précis).
Code
public static double exp1(double x) {
return (6+x*(6+x*(3+x)))*0.16666666f;
}
public static double exp2(double x) {
return (24+x*(24+x*(12+x*(4+x))))*0.041666666f;
}
public static double exp3(double x) {
return (120+x*(120+x*(60+x*(20+x*(5+x)))))*0.0083333333f;
}
public static double exp4(double x) {
return 720+x*(720+x*(360+x*(120+x*(30+x*(6+x))))))*0.0013888888f;
}
public static double exp5(double x) {
return (5040+x*(5040+x*(2520+x*(840+x*(210+x*(42+x*(7+x)))))))*0.00019841269f;
}
public static double exp6(double x) {
return (40320+x*(40320+x*(20160+x*(6720+x*(1680+x*(336+x*(56+x*(8+x))))))))*2.4801587301e-5;
}
public static double exp7(double x) {
return (362880+x*(362880+x*(181440+x*(60480+x*(15120+x*(3024+x*(504+x*(72+x*(9+x)))))))))*2.75573192e-6;
}
Précision
Function Error in [-1...1] Error in [3.14...3.14] exp1 0.05 1.8% 8.8742 38.40% exp2 0.01 0.36% 4.8237 20.80% exp3 0.0016152 0.59% 2.28 9.80% exp4 0.0002263 0.0083% 0.9488 4.10% exp5 0.0000279 0.001% 0.3516 1.50% exp6 0.0000031 0.00011% 0.1172 0.50% exp7 0.0000003 0.000011% 0.0355 0.15%
Crédits
Ces implémentations de exp() ont été calculées par "scoofy" en utilisant la série Taylor à partir d'une implémentation tanh() de "fuzzpilz" (quels qu'ils soient, je viens d'avoir ces références sur mon code).
Les approximations de la série Taylor (telles que les fonctions expX() dans la réponse de Adriano) sont les plus précises près de zéro et peuvent avoir d'énormes erreurs à -20 ou même -5. Si l'entrée a une plage connue, telle que -20 à 0 comme la question originale, vous pouvez utiliser une petite table de recherche et une multiplication supplémentaire pour améliorer considérablement la précision.
L'astuce consiste à reconnaître que exp() peut être séparé en parties entières et fractionnaires. Par exemple:
exp(-2.345) = exp(-2.0) * exp(-0.345)
La partie fractionnaire sera toujours être entre -1 et 1, donc une approximation de la série Taylor sera assez précise. La partie entière n'a que 21 valeurs possibles pour exp (-20) à exp (0), donc celles-ci peuvent être stockées dans une petite table de recherche.
J'ai étudié l'article de Nicol Schraudolph où l'implémentation C originale de la fonction ci-dessus a été définie plus en détail maintenant. Il semble qu'il n'est probablement pas possible d'approuver substantiellement la précision du calculexp sans affecter gravement les performances. D'autre part, l'approximation est également valable pour les grandes magnitudes de x, jusqu'à +/- 700, ce qui est bien sûr avantageux.
L'implémentation de La fonction ci-dessus est accordé pour obtenir une erreur quadratique moyenne minimale. Schraudolph décrit comment le terme additif dans l'expression tmp peut être modifié pour obtenir des propriétés d'approximation alternatives.
"exp" >= exp for all x 1072693248 - (-1) = 1072693249
"exp" <= exp for all x - 90253 = 1072602995
"exp" symmetric around exp - 45799 = 1072647449
Mimimum possible mean deviation - 68243 = 1072625005
Minimum possible root-mean-square deviation - 60801 = 1072632447
Il souligne également qu'à un niveau" microscopique " la fonction approximative "exp" présente un comportement de cas d'escalier puisque 32 bits sont ignorés dans la conversion de long à double . Cela signifie que la fonction est constante par pièce sur une très petite échelle, mais la fonction est au moins jamais diminuer avec l'augmentation x .
Le code suivant devrait répondre aux exigences de précision, car pour les entrées dans [-87,88] les résultats ont une erreur relative
Je suppose que puisque l'exigence de précision est faible, le calcul à une seule précision est correct. Un algorithme classique est utilisé dans lequel le calcul de exp () est mappé au calcul de exp2(). Après la conversion d'argument via la multiplication par log2 (e), l'exponentation par la partie fractionnaire est gérée à l'aide d'un polynôme minimax de degré 2, tandis que l'exponentation par la partie intégrale de l'argument est effectuée par manipulation directe de la partie exposant du nombre IEEE-754 de précision unique.
L'union volatile facilite la ré-interprétation d'un motif de bits comme un nombre entier ou un nombre à virgule flottante de précision unique, nécessaire à la manipulation de l'exposant. Il semble que C# offre des fonctions de ré-interprétation décriées pour cela, ce qui est beaucoup plus propre.
Les deux problèmes de performance potentiels sont la fonction floor () et la conversion float - > int. Traditionnellement, les deux étaient lents sur x86 en raison de la nécessité de gérer l'état du processeur dynamique. Mais SSE (en particulier SSE 4.1) fournit des instructions qui permettent à ces opérations d'être rapides. Je ne sais pas si C# peut utiliser ces instructions.
/* max. rel. error <= 1.73e-3 on [-87,88] */
float fast_exp (float x)
{
volatile union {
float f;
unsigned int i;
} cvt;
/* exp(x) = 2^i * 2^f; i = floor (log2(e) * x), 0 <= f <= 1 */
float t = x * 1.442695041f;
float fi = floorf (t);
float f = t - fi;
int i = (int)fi;
cvt.f = (0.3371894346f * f + 0.657636276f) * f + 1.00172476f; /* compute 2^f */
cvt.i += (i << 23); /* scale by 2^i */
return cvt.f;
}