Algorithme rapide pour calculer les percentiles afin d'éliminer les valeurs aberrantes
j'ai un programme qui a besoin de calculer à plusieurs reprises le centile approximatif (ordre statistique) d'un ensemble de données afin de supprimer les valeurs aberrantes avant de poursuivre le traitement. Je le fais actuellement en triant le tableau des valeurs et en choisissant l'élément approprié; c'est faisable, mais c'est un blip perceptible sur les profils malgré être une partie assez mineure du programme.
Plus d'info:
- Le jeu de données contient de l'ordre de 100000 virgule flottante les nombres, et supposé être" raisonnablement " distribué - il est peu probable d'avoir des doublons ou des pics énormes de densité près de valeurs particulières; et si pour une raison étrange la distribution est étrange, il est correct pour une approximation d'être moins précis puisque les données est probablement foiré de toute façon et le traitement ultérieur douteux. Cependant, les données ne sont pas nécessairement distribuées de façon uniforme ou normale; il est tout simplement très peu probable qu'elles soient dégénérées.
- Une solution approximative serait bien, mais je ne besoin de comprendre comment l'approximation introduit une erreur pour s'assurer qu'elle est valide.
- comme le but est d'éliminer les valeurs aberrantes, Je calcule deux percentiles par rapport aux mêmes données en tout temps: par exemple, un à 95% et un à 5%.
- l'application est en C# avec des bits de levage lourd en C++; le pseudocode ou une bibliothèque préexistante dans l'un ou l'autre serait très bien.
- une façon entièrement différente d'éliminer les valeurs aberrantes serait également acceptable, du moment que raisonnable.
- mise à Jour: Il semble que je suis à la recherche d'une approximation algorithme de sélection.
bien que tout cela soit fait en boucle, les données sont (légèrement) différentes à chaque fois, il n'est donc pas facile de réutiliser une infrastructure de données comme cela a été fait pour cette question.
Solution Implémentée
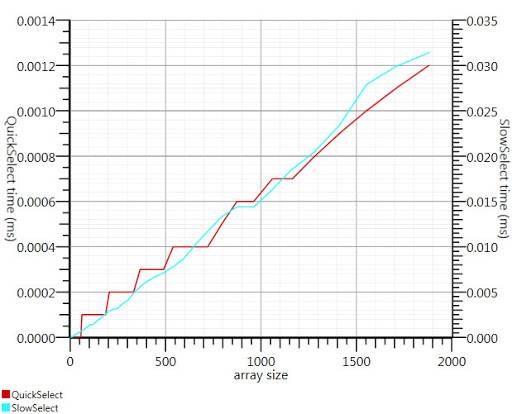
en utilisant l'algorithme de sélection de wikipedia comme suggéré par Gronim réduit cette partie de la temps de passage d'un facteur 20.
comme je n'ai pas pu trouver d'implémentation C#, voici ce que j'ai trouvé. Il est plus rapide même pour les petites entrées que le tableau.Et à 1000 éléments, c'est 25 fois plus rapide.
public static double QuickSelect(double[] list, int k) {
return QuickSelect(list, k, 0, list.Length);
}
public static double QuickSelect(double[] list, int k, int startI, int endI) {
while (true) {
// Assume startI <= k < endI
int pivotI = (startI + endI) / 2; //arbitrary, but good if sorted
int splitI = partition(list, startI, endI, pivotI);
if (k < splitI)
endI = splitI;
else if (k > splitI)
startI = splitI + 1;
else //if (k == splitI)
return list[k];
}
//when this returns, all elements of list[i] <= list[k] iif i <= k
}
static int partition(double[] list, int startI, int endI, int pivotI) {
double pivotValue = list[pivotI];
list[pivotI] = list[startI];
list[startI] = pivotValue;
int storeI = startI + 1;//no need to store @ pivot item, it's good already.
//Invariant: startI < storeI <= endI
while (storeI < endI && list[storeI] <= pivotValue) ++storeI; //fast if sorted
//now storeI == endI || list[storeI] > pivotValue
//so elem @storeI is either irrelevant or too large.
for (int i = storeI + 1; i < endI; ++i)
if (list[i] <= pivotValue) {
list.swap_elems(i, storeI);
++storeI;
}
int newPivotI = storeI - 1;
list[startI] = list[newPivotI];
list[newPivotI] = pivotValue;
//now [startI, newPivotI] are <= to pivotValue && list[newPivotI] == pivotValue.
return newPivotI;
}
static void swap_elems(this double[] list, int i, int j) {
double tmp = list[i];
list[i] = list[j];
list[j] = tmp;
}
Merci, Gronim, de m'avoir montré la bonne direction!
10 réponses
la solution d'Henrik pour l'histogramme fonctionnera. Vous pouvez également utiliser un algorithme de sélection pour trouver efficacement les K éléments les plus grands ou les plus petits dans un tableau de N éléments dans O(n). Pour utiliser ceci pour le 95e percentile K=0.05 n et trouver les k plus grands éléments.
Référence:
http://en.wikipedia.org/wiki/Selection_algorithm#Selecting_k_smallest_or_largest_elements
Selon à son créateur, un SoftHeap peut être utilisé pour:
calcul exact ou approximatif médianes et percentiles de façon optimale. Il est également utile pour le tri approximatif...
vous pouvez estimer vos percentiles à partir d'une partie seulement de votre ensemble de données, comme les premiers quelques milliers de points.
théorème de Glivenko–Cantelli assure que ce serait une assez bonne estimation, si vous pouvez supposer que vos points de données sont indépendants.
j'ai utilisé pour identifier les valeurs aberrantes en calculant le écart-type. Tout ce qui est à une distance supérieure à 2 (ou 3) fois l'écart-type par rapport à l'avarage est une valeur aberrante. 2 fois = environ 95%.
puisque vous calculez l'avarage, il est également très facile de calculer l'écart-type est très rapide.
Vous pouvez également utiliser uniquement un sous-ensemble de vos données pour calculer les nombres.
divisez l'intervalle entre le minimum et le maximum de vos données en (disons) 1000 bacs et calculez un histogramme. Puis construisez des sommes partielles et voyez où elles dépassent d'abord 5000 ou 95000.
il y a quelques approches de base auxquelles je peux penser. La première consiste à calculer la fourchette (en trouvant les valeurs les plus élevées et les plus basses), à projeter chaque élément à un percentile ((x - min) / fourchette) et à jeter tous ceux qui évaluent à plus bas que .05 ou supérieur .95.
de 97,5 percentile. Le calcul de la moyenne d'une série est linéaire, comme c'est la norme dev (racine carrée de la somme de la différence de chaque élément et de la moyenne). Ensuite, soustrayez 2 sigmas de la moyenne, et ajouter 2 sigmas à la moyenne, et vous avez vos limites des valeurs aberrantes.les deux vont calculer en temps à peu près linéaire; le premier nécessite deux passes, le second en prend trois (une fois que vous avez vos limites, vous devez toujours écarter les valeurs aberrantes). Puisque c'est une liste de base opération, Je ne pense pas que vous trouverez quoi que ce soit avec la complexité logarithmique ou constante; tout gain de performance supplémentaire exigerait soit l'optimisation de l'itération et le calcul, ou l'introduction d'erreur en effectuant les calculs sur un sous-échantillon (tel que chaque troisième élément).
une bonne réponse générale à votre problème semble être RANSAC.
Avec un modèle, et quelques données bruyantes, l'algorithme récupère efficacement les paramètres du modèle.
Vous aurez à choisir un modèle simple qui permet de cartographier vos données. Tout ce qui est lisse devrait être parfait. Disons un mélange de quelques gaussiens. RANSAC définira les paramètres de votre modèle et estimera un ensemble d'inliners en même temps. Alors jette ce qui ne va pas avec le modèle.
vous pouvez filtrer 2 ou 3 écarts-types même si les données ne sont pas normalement distribuées; au moins, cela sera fait de manière cohérente, ce qui devrait être important.
lorsque vous retirez les valeurs aberrantes, le dev std va changer, vous pouvez le faire en boucle jusqu'à ce que le changement dans le dev std soit minime. Si oui ou non vous voulez faire cela dépend de pourquoi vous manipulez les données de cette façon. Certains statisticiens émettent des réserves importantes quant à la suppression des valeurs aberrantes. Mais certains suppriment les valeurs aberrantes de prouver que les données sont assez normalement distribués.
Pas un expert, mais ma mémoire suggère:
- pour déterminer exactement les points de percentile, vous devez trier et Compter
- prendre un échantillon des données et calculer les valeurs de percentile ressemble à un bon plan pour une approximation décente si vous pouvez obtenir un bon échantillon
- si non, comme suggéré par Henrik, vous pouvez éviter la pleine trier si vous ne les seaux et les compter
un ensemble de données d'éléments de 100k ne prend presque pas de temps à trier, donc je suppose que vous devez le faire à plusieurs reprises. Si le jeu de données est le même que celui qui vient d'être légèrement mis à jour, il est préférable de construire un arbre (O(N log N)) et ensuite la suppression et l'ajout de nouveaux points d'arrivée (O(K log N) où K est le nombre de points changé). Sinon, le k e solution d'élément le plus grand déjà mentionnée vous donne O(N) pour chaque ensemble de données.