Expansion remplissage de polygone convexe

pour agrandir un polygone convexe, tracer une ligne parallèle à chaque bord et au nombre donné d'unités. Ensuite, utilisez les points d'intersection des nouvelles lignes comme les sommets du polygone élargi. Le javascript / canvas à la fin suit cette décomposition fonctionnelle:

Étape 1: déterminez quel côté est "sorti

L'ordre des sommets (points) question. Dans un polygone convexe, elles peuvent être classées dans le sens des aiguilles d'une montre (CW) ou dans le sens contraire des aiguilles d'une montre (CCW). Dans un polygone CW, tourner l'un des bords de 90 degrés CCW pour obtenir une normale orientée vers l'extérieur. Sur un polygone CCW, tournez le CW à la place.

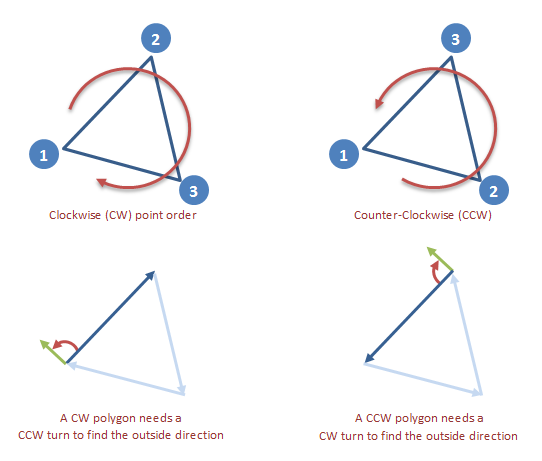
si la direction de virage des sommets n'est pas connue à l'avance, examiner comment le deuxième bord tourne à partir du premier. Dans un polygone convexe, les bords restants continueront à tourner dans la même direction:

1. trouver le CW normal du premier bord . Nous ne savons pas encore si c'est vers l'intérieur ou vers l'extérieur.

2. calculez le produit de point du deuxième bord avec la normale nous avons calculé. Si le deuxième bord tourne CW, le produit dot sera positif. Il sera négatif autrement.

"1519140920 des Mathématiques":

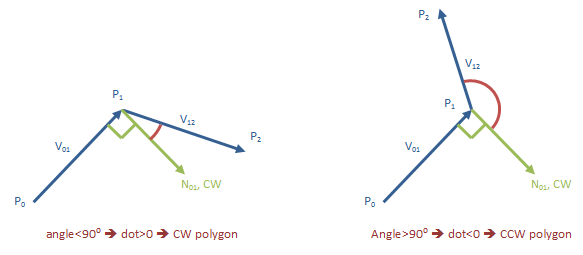
// in vector terms:
v01 = p1 - p0                      // first edge, as a vector
v12 = p2 - p1                      // second edge, as a vector
n01 = (v01.y, -v01.x)              // CW normal of first edge
d = v12 * n01                      // dot product

// and in x,y terms:
v01 = (p1.x-p0.x, p1.y-p0.y)       // first edge, as a vector
v12 = (p2.x-p1.x, p2.y-p1.y)       // second edge, as a vector
n01 = (v01.y, -v01.x)              // CW normal of first edge
d = v12.x * n01.x + v12.y * n01.y; // dot product: v12 * n01

if (d > 0) {
    // the polygon is CW
} else {
    // the polygon is CCW
}

// and what if d==0 ?
// -- that means the second edge continues in the same
// direction as a first.  keep looking for an edge that
// actually turns either CW or CCW.

Code:

function vecDot(v1, v2) {
    return v1.x * v2.x + v1.y * v2.y;
}

function vecRot90CW(v) {
    return { x: v.y, y: -v.x };
}

function vecRot90CCW(v) {
    return { x: -v.y, y: v.x };
}

function polyIsCw(p) {
    return vecDot(
        vecRot90CW({ x: p[1].x - p[0].x, y: p[1].y - p[0].y }),
        { x: p[2].x - p[1].x, y: p[2].y - p[1].y }) >= 0;
}

var rot = polyIsCw(p) ? vecRot90CCW : vecRot90CW;

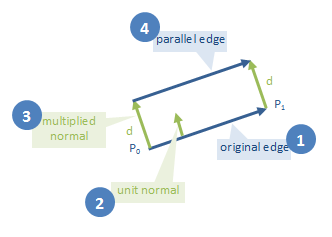
Étape 2: Trouver des lignes parallèles aux bords du polygone

maintenant que nous savons quel côté est sorti, nous pouvons calculer des lignes parallèles à chaque bord de polygone, à exactement la distance requise. Voici notre stratégie:

1. pour chaque arête, calculer sa normale orientée vers l'extérieur

2. normaliser la normale, telle que sa longueur devient une unité

3. multipliez la normale par la distance que nous voulons que le polygone étendu soit de l'original

4. ajouter la normale multipliée aux deux extrémités du bord. Qui nous donner deux points sur la ligne parallèle. Ces deux points suffisent à définir la ligne parallèle.

Code:

// given two vertices pt0 and pt1, a desired distance, and a function rot()
// that turns a vector 90 degrees outward:

function vecUnit(v) {
    var len = Math.sqrt(v.x * v.x + v.y * v.y);
    return { x: v.x / len, y: v.y / len };
}

function vecMul(v, s) {
    return { x: v.x * s, y: v.y * s };
}

var v01 = { x: pt1.x - pt0.x, y: pt1.y - pt0.y };  // edge vector
var d01 = vecMul(vecUnit(rot(v01)), distance);     // multiplied unit normal
var ptx0 = { x: pt0.x + d01.x, y: pt0.y + d01.y }; // two points on the
var ptx1 = { x: pt1.x + d01.x, y: pt1.y + d01.y }; //     parallel line

Étape 3: calculer les intersections des lignes parallèles

--ce sont les sommets du polygone élargi.

"1519140920 des Mathématiques":

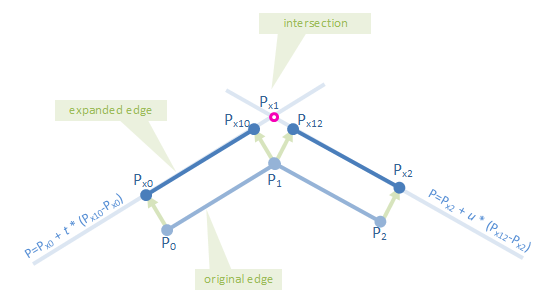
Une droite passant par deux points P1 , P2 peut être décrit comme:

P = P1 + t * (P2 - P1)

deux lignes peuvent être décrites comme

P = P1 + t * (P2 - P1)
P = P3 + u * (P4 - P3)

et leur intersection doit être sur les deux lignes:

P = P1 + t * (P2 - P1) = P3 + u * (P4 - P3)

cela peut être massé pour ressembler à:

(P2 - P1) * t + (P3 - P4) * u = P3 - P1

qui en termes de x, y est:

(P2.x - P1.x) * t + (P3.x - P4.x) * u = P3.x - P1.x
(P2.y - P1.y) * t + (P3.y - P4.y) * u = P3.y - P1.y

comme les points P1, P2, P3 et P4 sont connus, il en va de même pour les valeurs suivantes:

a1 = P2.x - P1.x    a2 = P2.y - P1.y
b1 = P3.x - P4.x    b2 = P3.y - P4.y
c1 = P3.x - P1.x    c2 = P3.y - P1.y

cela raccourcit nos équations à:

a1*t + b1*u = c1
a2*t + b2*u = c2    

Résoudre t devient:

t = (b1*c2 - b2*c1)/(a2*b1 - a1*b2)

qui nous permet de trouver l'intersection à P = P1 + t * (P2 - P1) .

Code:

function intersect(line1, line2) {
    var a1 = line1[1].x - line1[0].x;
    var b1 = line2[0].x - line2[1].x;
    var c1 = line2[0].x - line1[0].x;

    var a2 = line1[1].y - line1[0].y;
    var b2 = line2[0].y - line2[1].y;
    var c2 = line2[0].y - line1[0].y;

    var t = (b1*c2 - b2*c1) / (a2*b1 - a1*b2);

    return {
        x: line1[0].x + t * (line1[1].x - line1[0].x),
        y: line1[0].y + t * (line1[1].y - line1[0].y)
    };
}

Étape 4: Traiter avec cas particuliers

il y a un certain nombre de cas spéciaux qui méritent notre attention. Laissé comme exercice au lecteur...

1. Lorsqu'il y a un angle très prononcé entre deux arêtes, le vertex étendu peut être très loin de l'original. Vous pourriez envisager de couper le bord élargi si elle va au-delà d'un certain seuil. Dans le cas extrême, l'angle est zéro, ce qui suggère que le vertex étendu est à l'infini, provoquant la division par zéro dans l'arithmétique. Watch out.

2. quand les deux premiers bords sont sur la même ligne, on ne peut pas dire si c'est un polygone CW ou CCW en les regardant. Regardez plus de bords.

3. les polygones non convexes sont beaucoup plus intéressants... et ne sont pas abordés ici.

échantillon complet code

déposez ceci dans un navigateur à Toile. J'ai utilisé Chrome 6 sur Windows. Le triangle et sa version élargie devraient s'animer.

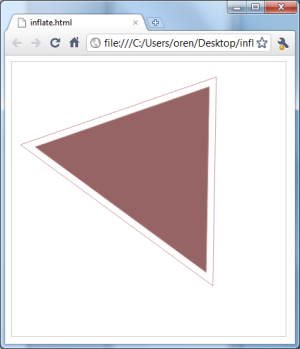
<html>
    <head>
            <style type="text/css">
                canvas { border: 1px solid #ccc; }
            </style>
            <script type="text/javascript" src="http://ajax.googleapis.com/ajax/libs/jquery/1.4.2/jquery.min.js"></script>
            <script type="text/javascript">
                $(function() {
                    var canvas = document.getElementById('canvas');  
                    if (canvas.getContext) {  
                        var context = canvas.getContext('2d');  

                        // math for expanding a polygon

                        function vecUnit(v) {
                            var len = Math.sqrt(v.x * v.x + v.y * v.y);
                            return { x: v.x / len, y: v.y / len };
                        }

                        function vecMul(v, s) {
                            return { x: v.x * s, y: v.y * s };
                        }

                        function vecDot(v1, v2) {
                            return v1.x * v2.x + v1.y * v2.y;
                        }

                        function vecRot90CW(v) {
                            return { x: v.y, y: -v.x };
                        }

                        function vecRot90CCW(v) {
                            return { x: -v.y, y: v.x };
                        }

                        function intersect(line1, line2) {
                            var a1 = line1[1].x - line1[0].x;
                            var b1 = line2[0].x - line2[1].x;
                            var c1 = line2[0].x - line1[0].x;

                            var a2 = line1[1].y - line1[0].y;
                            var b2 = line2[0].y - line2[1].y;
                            var c2 = line2[0].y - line1[0].y;

                            var t = (b1*c2 - b2*c1) / (a2*b1 - a1*b2);

                            return {
                                x: line1[0].x + t * (line1[1].x - line1[0].x),
                                y: line1[0].y + t * (line1[1].y - line1[0].y)
                            };
                        }

                        function polyIsCw(p) {
                            return vecDot(
                                vecRot90CW({ x: p[1].x - p[0].x, y: p[1].y - p[0].y }),
                                { x: p[2].x - p[1].x, y: p[2].y - p[1].y }) >= 0;
                        }

                        function expandPoly(p, distance) {
                            var expanded = [];
                            var rot = polyIsCw(p) ? vecRot90CCW : vecRot90CW;

                            for (var i = 0; i < p.length; ++i) {

                                // get this point (pt1), the point before it
                                // (pt0) and the point that follows it (pt2)
                                var pt0 = p[(i > 0) ? i - 1 : p.length - 1];
                                var pt1 = p[i];
                                var pt2 = p[(i < p.length - 1) ? i + 1 : 0];

                                // find the line vectors of the lines going
                                // into the current point
                                var v01 = { x: pt1.x - pt0.x, y: pt1.y - pt0.y };
                                var v12 = { x: pt2.x - pt1.x, y: pt2.y - pt1.y };

                                // find the normals of the two lines, multiplied
                                // to the distance that polygon should inflate
                                var d01 = vecMul(vecUnit(rot(v01)), distance);
                                var d12 = vecMul(vecUnit(rot(v12)), distance);

                                // use the normals to find two points on the
                                // lines parallel to the polygon lines
                                var ptx0  = { x: pt0.x + d01.x, y: pt0.y + d01.y };
                                var ptx10 = { x: pt1.x + d01.x, y: pt1.y + d01.y };
                                var ptx12 = { x: pt1.x + d12.x, y: pt1.y + d12.y };
                                var ptx2  = { x: pt2.x + d12.x, y: pt2.y + d12.y };

                                // find the intersection of the two lines, and
                                // add it to the expanded polygon
                                expanded.push(intersect([ptx0, ptx10], [ptx12, ptx2]));
                            }
                            return expanded;
                        }

                        // drawing and animating a sample polygon on a canvas

                        function drawPoly(p) {
                            context.beginPath();
                            context.moveTo(p[0].x, p[0].y);
                            for (var i = 0; i < p.length; ++i) {
                                context.lineTo(p[i].x, p[i].y);
                            }
                            context.closePath();
                            context.fill();
                            context.stroke();
                        }

                        function drawPolyWithMargin(p, margin) {
                            context.fillStyle = "rgb(255,255,255)";  
                            context.strokeStyle = "rgb(200,150,150)";  
                            drawPoly(expandPoly(p, margin));

                            context.fillStyle = "rgb(150,100,100)";  
                            context.strokeStyle = "rgb(200,150,150)";  
                            drawPoly(p);
                        }

                        var p = [{ x: 100, y: 100 }, { x: 200, y: 120 }, { x: 80, y: 200 }];
                        setInterval(function() {
                            for (var i in p) {
                                var pt = p[i];
                                if (pt.vx === undefined) {
                                    pt.vx = 5 * (Math.random() - 0.5);
                                    pt.vy = 5 * (Math.random() - 0.5);
                                }

                                pt.x += pt.vx;
                                pt.y += pt.vy;

                                if (pt.x < 0 || pt.x > 400) { pt.vx = -pt.vx; }
                                if (pt.y < 0 || pt.y > 400) { pt.vy = -pt.vy; }
                            }
                            context.clearRect(0, 0, 800, 400);
                            drawPolyWithMargin(p, 10);
                        }, 50);
                    }
                });
            </script>
    </head>
    <body>
        <canvas id="canvas" width="400" height="400"></canvas>  
    </body>
</html>

exemple de code disclaimers:

• l'échantillon sacrifie une certaine efficacité pour la clarté. Dans votre code, vous pouvez calculer chaque bord élargi parallèle, juste une fois et pas deux comme ici

• la coordonnée y de la toile se développe vers le bas, ce qui inverse la logique CW/CCW. Les choses continuent de fonctionner cependant car nous avons juste besoin de tourner les normales vers l'extérieur dans une direction opposée à celle du polygone -- et les deux sont renversés.