Distribuer uniformément n points sur une sphère
j'ai besoin d'un algorithme qui puisse me donner des positions autour d'une sphère pour N points (moins de 20, probablement) qui les étalent vaguement. Il n'y a pas besoin de "perfection", mais j'en ai juste besoin pour qu'aucun d'eux ne soit groupé.
- cette question fournit un bon code, mais je n'ai pas pu trouver un moyen de rendre cet uniforme, car cela semblait 100% aléatoire.
- cet article de blog recommandé avait deux façons de permettre l'entrée du nombre de points sur la sphère, mais le SAFF et Kuijlaars algorithme est exactement en psuedocode je pourrais transcrire, et le exemple de code j'ai trouvé contenu "noeud[k]", que je ne pouvais pas voir expliqué et ruiné cette possibilité. Le deuxième exemple de blog était le Golden Section Spiral, qui m'a donné des résultats étranges, groupés, sans aucune façon claire de définir un rayon constant.
- This algorithme de cette question semble comme il pourrait éventuellement fonctionner, mais je ne peux pas assembler ce qui est sur cette page dans psuedocode ou quoi que ce soit.
quelques autres sujets de questions que j'ai rencontrés ont parlé de la distribution uniforme aléatoire, ce qui ajoute un niveau de complexité qui ne me préoccupe pas. Je m'excuse que c'est une question idiote, mais je voulais montrer que j'ai vraiment bien cherché et encore trouver à court.
donc, ce que je cherche c'est un pseudo simple pour distribuer uniformément N points autour d'une sphère d'unité, qui retourne soit en coordonnées sphériques ou cartésiennes. Encore mieux si elle peut même distribuer avec un peu de randomisation (pensez planètes autour d'une étoile, convenablement étalées, mais avec de la marge de manœuvre).
14 réponses
dans ce code d'exemple node[k] est juste le noeud kth. Vous générez un tableau N points et node[k] est le kth (de 0 à N-1). Si c'est tout ce qui te perturbe, j'espère que tu pourras l'utiliser maintenant.
(en d'autres termes, k est un tableau de taille N qui est défini avant le début du fragment de code, et qui contient une liste des points).
alternativement , en s'appuyant sur l'autre réponse ici (et en utilisant Python):
> cat ll.py
from math import asin
nx = 4; ny = 5
for x in range(nx):
lon = 360 * ((x+0.5) / nx)
for y in range(ny):
midpt = (y+0.5) / ny
lat = 180 * asin(2*((y+0.5)/ny-0.5))
print lon,lat
> python2.7 ll.py
45.0 -166.91313924
45.0 -74.0730322921
45.0 0.0
45.0 74.0730322921
45.0 166.91313924
135.0 -166.91313924
135.0 -74.0730322921
135.0 0.0
135.0 74.0730322921
135.0 166.91313924
225.0 -166.91313924
225.0 -74.0730322921
225.0 0.0
225.0 74.0730322921
225.0 166.91313924
315.0 -166.91313924
315.0 -74.0730322921
315.0 0.0
315.0 74.0730322921
315.0 166.91313924
si vous tracez cela, vous verrez que l'espacement vertical est plus grand près des pôles de sorte que chaque point est situé dans environ le même total superficie de l'espace (près des pôles Il ya moins d'espace" horizontalement", donc il donne plus"verticalement").
ce n'est pas la même chose que tous les points ayant à peu près la même distance à leurs voisins (ce qui est ce que je pense que votre les liens sont en parler), mais il peut être suffisant pour ce que vous voulez et améliore simplement faire un uniforme grille de latitude/longitude.
L'algorithme de la sphère de Fibonacci est parfait pour cela. C'est rapide et donne des résultats en un coup d'oeil facilement tromper l'œil humain. vous pouvez voir un exemple fait avec le traitement qui montrera le résultat au fil du temps que des points sont ajoutés. voici un autre grand exemple interactif réalisé par @gman. Et voici une version rapide de python avec une option de randomisation simple:
import math, random
def fibonacci_sphere(samples=1,randomize=True):
rnd = 1.
if randomize:
rnd = random.random() * samples
points = []
offset = 2./samples
increment = math.pi * (3. - math.sqrt(5.));
for i in range(samples):
y = ((i * offset) - 1) + (offset / 2);
r = math.sqrt(1 - pow(y,2))
phi = ((i + rnd) % samples) * increment
x = math.cos(phi) * r
z = math.sin(phi) * r
points.append([x,y,z])
return points
1000 échantillons vous donne ceci:
c'est ce qu'on appelle des points d'emballage sur une sphère, et il n'y a pas de solution (connue) générale, parfaite. Cependant, il y a beaucoup de solutions imparfaites. Les trois plus populaires semblent être:
- créer une simulation . Traiter chaque point comme un électron limitée à une sphère, puis exécuter une simulation pour un certain nombre d'étapes. La répulsion des électrons va naturellement tendre le système à un état plus stable, où les points sont aussi loin l'un de l'autre qu'ils peuvent l'être.
- Hypercube rejet . Cette méthode fantaisiste est en fait très simple: vous choisissez uniformément les points (beaucoup plus que
nd'entre eux) à l'intérieur du cube entourant la sphère, puis rejeter les points à l'extérieur de la sphère. Traitez les points restants comme des vecteurs et normalisez-les. Ce sont vos "échantillons" - choisisseznd'entre eux en utilisant une méthode (au hasard, gourmand, etc). - Spirale approximations . Vous tracez une spirale autour d'une sphère, et répartissez uniformément les points autour de la spirale. En raison des mathématiques impliquées, celles-ci sont plus compliquées à comprendre que la simulation, mais beaucoup plus rapide (et impliquant probablement moins de code). Le plus populaire semble être en Saff, et al .
Un beaucoup plus des informations sur ce problème peut être trouvé ici
La spirale d'or de la méthode
vous avez dit que vous ne pouviez pas obtenir la méthode Golden spiral pour travailler et c'est une honte parce que c'est vraiment, vraiment bon. Je tiens à vous donner une compréhension complète de sorte que vous pouvez peut-être comprendre comment garder cette loin d'être "retroussé."
donc voici une façon rapide, non-aléatoire de créer un réseau qui est approximativement correct; comme discuté ci-dessus, aucun réseau ne sera parfait, mais cela peut être "assez bon". Il est comparé à d'autres méthodes par exemple à BendWavy.org mais il a juste un beau et joli look ainsi que d'une garantie sur l'espacement uniforme dans la limite.
Primer: tournesol spirales sur l'unité de disque
pour comprendre cet algorithme, je vous invite d'abord à regarder l'algorithme 2D spiral de tournesol. Ceci est basé sur le fait que la plupart des nombre irrationnel est le nombre d'or (1 + sqrt(5))/2 et si on émet points par l'approche " se tenir au centre, tourner un ratio d'or de tours entiers, puis émettre un autre point dans cette direction," on construit naturellement une spirale qui, comme vous arrivez à un nombre de plus en plus élevé de points, refuse néanmoins d'avoir des "barres" bien définies que les points s'alignent sur. (Note 1.)
l'algorithme pour l'espacement Pair sur un disque est,
from numpy import pi, cos, sin, sqrt, arange
import matplotlib.pyplot as pp
num_pts = 100
indices = arange(0, num_pts, dtype=float) + 0.5
r = sqrt(indices/num_pts)
theta = pi * (1 + 5**0.5) * indices
pp.scatter(r*cos(theta), r*sin(theta))
pp.show()
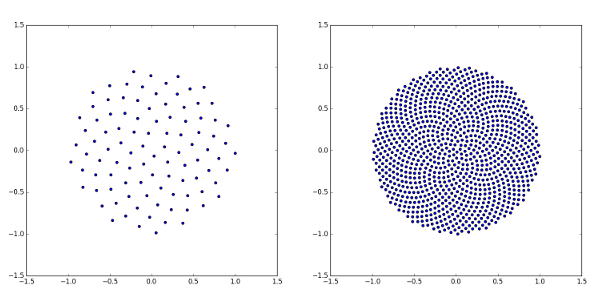
et il produit des résultats qui ressemblent à (n=100 et n = 1000):
espacement des points radialement
la chose clé étrange est la formule r = sqrt(indices / num_pts) ; comment en suis-je arrivé là? (Note 2.)
Eh bien, j'utilise la racine carrée ici parce que je veux que ceux-ci aient un espacement de surface égale autour de la sphère. C'est la même chose que de dire que dans la limite des grandes N je veux une petite région R ∈ ( r , r + d r ), Θ ∈ ( θ , θ + d θ ) pour contenir un nombre de points proportionnel à sa surface, qui est r d r d θ . Maintenant, si nous prétendons que nous sommes en parlant d'une variable aléatoire ici, ceci a une interprétation simple comme disant que la densité de probabilité conjointe pour ( R , Θ ) est juste C r pour une certaine constante c . La normalisation sur le disque unitaire force alors c = 1/π.
laissez-moi vous présenter un truc. Il vient de la théorie des probabilités où il est connu comme échantillonnage l'inverse CDF : supposons que vous vouliez générer une variable aléatoire avec une densité de probabilité f ( z ) et vous avez une variable aléatoire U ~ uniforme(0, 1), tout comme sort de random() dans la plupart des langues de programmation. Comment faites-vous cela?
- d'abord, Transformez votre densité en une fonction de distribution cumulative F ( z ), qui, rappelons-le, augmente monotoniquement de 0 à 1 avec la dérivée f ( z ).
- puis calculer la fonction inverse de CDF F -1 ( z ).
- vous trouverez que Z = F -1 ( U ) est distribué en fonction de la densité cible. (Note 3).
maintenant le rapport d'or spiral spaces les points dans un motif bien uniforme pour θ alors intégrons cela; pour le cercle de l'unité nous sommes laissés avec F ( r ) = r 2 . Donc la fonction inverse est F -1 ( u ) = u 1/2 , et donc nous générerions des points aléatoires sur la sphère en coordonnées polaires avec r = sqrt(random()); theta = 2 * pi * random() .
maintenant au lieu de au hasard échantillonnage Cette fonction inverse nous sommes uniformément échantillonnage il, et la chose agréable à propos de l'échantillonnage uniforme est que nos résultats sur la façon dont les points sont étalés dans la limite des grands N se comporteront comme si nous l'avions échantillonné au hasard. Cette combinaison est le truc. Au lieu de random() , nous utilisons (arange(0, num_pts, dtype=float) + 0.5)/num_pts , de sorte que, disons, si nous voulons échantillonner 10 points, ils sont r = 0.05, 0.15, 0.25, ... 0.95 . Nous échantillonnons uniformément r pour obtenir l'espacement de surface égale, et nous utilisons l'incrément de tournesol pour éviter d'horribles "barres" de points dans la production.
Maintenant le tournesol sur une sphère
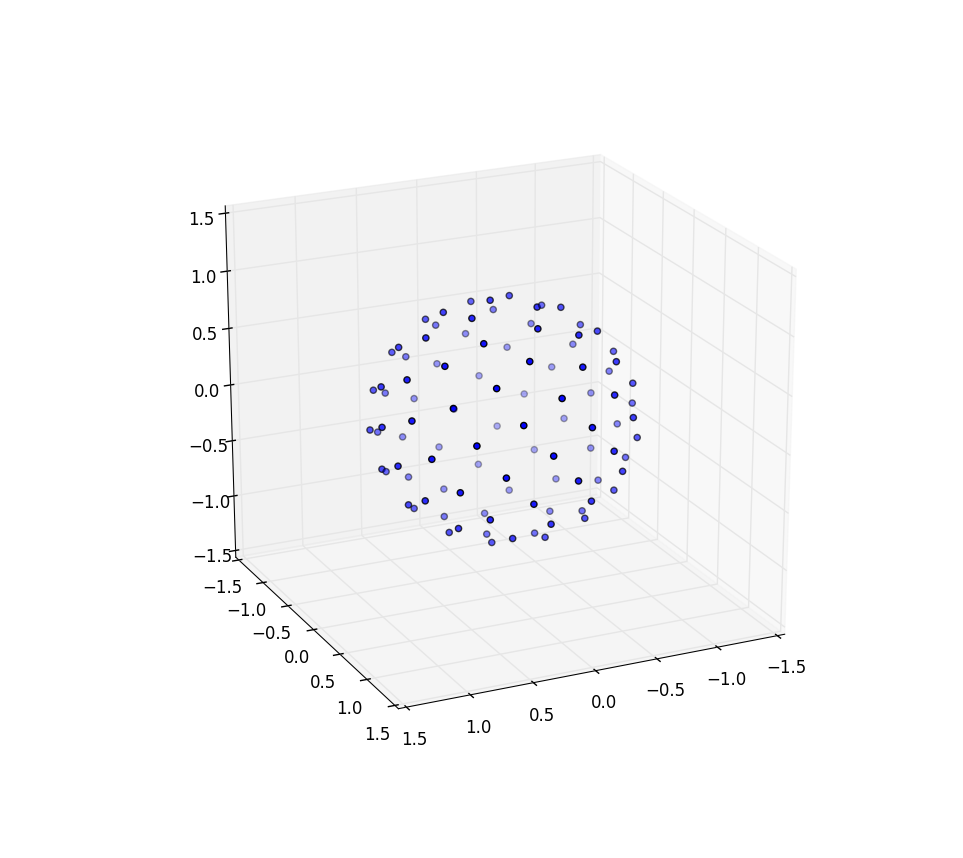
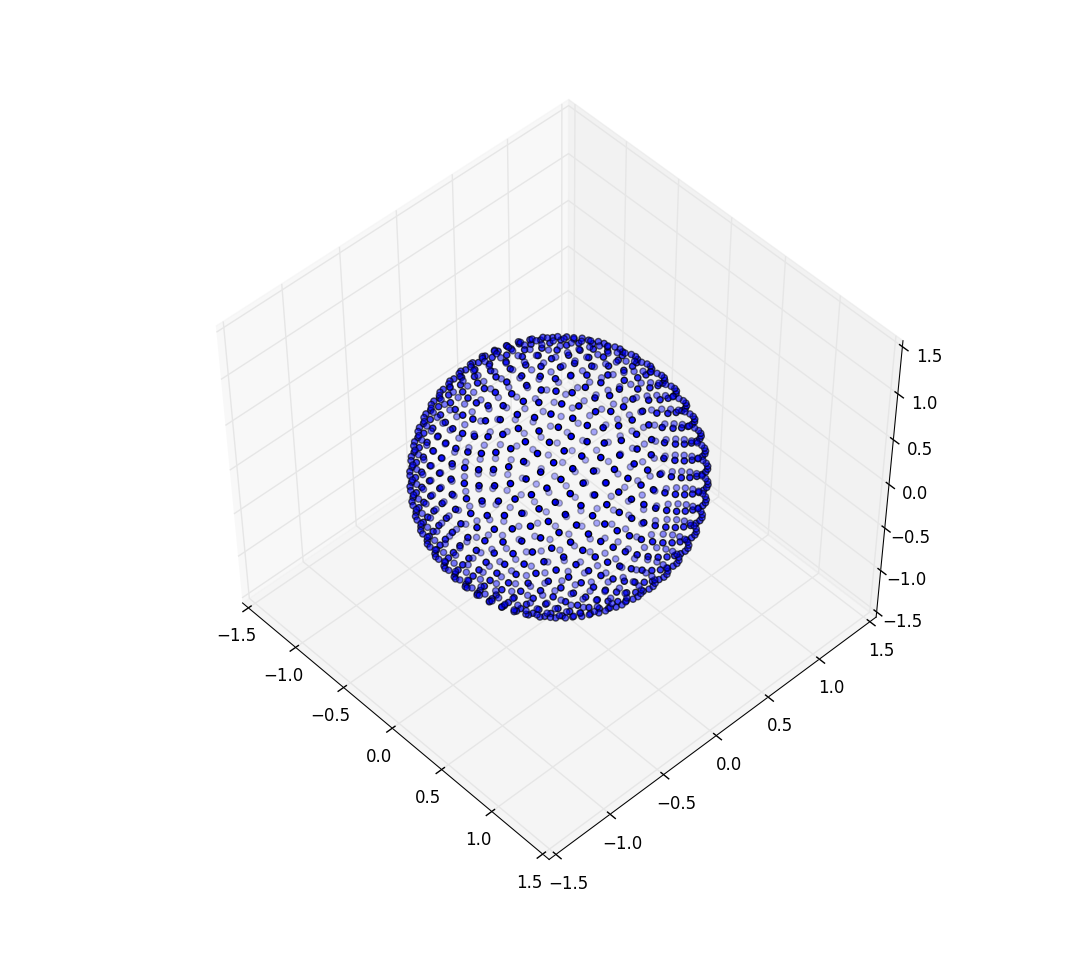
les changements que nous devons faire pour marquer la sphère avec des points impliquent simplement la commutation des coordonnées polaires pour les coordonnées sphériques. Bien sûr, la coordonnée radiale n'entre pas là-dedans parce que nous sommes sur une sphère d'unité. Pour garder les choses un peu plus cohérente ici, même si j'ai été formé comme un physicien, je vais utiliser les coordonnées des mathématiciens où 0 ≤ φ ≤ π est la latitude descendant du pôle et 0 ≤ θ ≤ 2π est la longitude. Donc la différence par rapport à ce qui précède est que nous sommes en train de remplacer la variable r par φ .
notre élément de surface, qui était R d r d θ , devient maintenant le péché pas-beaucoup-plus-compliqué ( φ ) d φ d ". Donc, notre commune densité pour l'espacement uniforme est sin ( φ ) /4π. En intégrant θ , on trouve f ( φ ) = péché( φ )/2, donc F ( φ ) = (1 - cos( φ ))/2. En inversant cela, nous pouvons voir qu'une variable aléatoire uniforme ressemblerait à acos (1-2 u ), mais nous échantillonnons uniformément au lieu d'au hasard, de sorte que nous utilisez plutôt φ "15192070920 k = acos(1-2 ( k + 0.5)/ N ). Et le reste de l'algorithme projette ceci sur les coordonnées x, y et z:
from numpy import pi, cos, sin, arccos, arange
import mpl_toolkits.mplot3d
import matplotlib.pyplot as pp
num_pts = 1000
indices = arange(0, num_pts, dtype=float) + 0.5
phi = arccos(1 - 2*indices/num_pts)
theta = pi * (1 + 5**0.5) * indices
x, y, z = cos(theta) * sin(phi), sin(theta) * sin(phi), cos(phi);
pp.figure().add_subplot(111, projection='3d').scatter(x, y, z);
pp.show()
encore une fois pour n = 100 et n = 1000 les résultats ressemblent:
Notes
-
Ces "barres" sont formées par des approximations rationnelles à un nombre, et les meilleures approximations rationnelles à un nombre proviennent de son expression de fraction continue,
z + 1/(n_1 + 1/(n_2 + 1/(n_3 + ...)))oùzest un entier etn_1, n_2, n_3, ...est soit une suite finie ou infinie d'entiers positifs:def continued_fraction(r): while r != 0: n = floor(r) yield n r = 1/(r - n)puisque la partie de fraction
1/(...)est toujours entre zéro et un, un grand entier dans la fraction continue permet une approximation rationnelle particulièrement bonne: "Un divisé par quelque chose entre 100 et 101" est mieux que "un divisé par quelque chose entre 1 et 2."Le nombre le plus irrationnel est donc celui qui est1 + 1/(1 + 1/(1 + ...))et n'a pas d'approximations rationnelles particulièrement bonnes; on peut résoudre φ = 1 + 1/ φ en multipliant par φ pour obtenir la formule du ratio d'or.-
pour les gens qui ne sont pas si familiers avec NumPy -- toutes les fonctions sont "vectorisées", de sorte que
sqrt(array)est le même que ce que d'autres langues pourraient écriremap(sqrt, array). Il s'agit donc d'une application composant-par-composantsqrt. Il en va de même pour la division par un scalaire ou l'addition avec des scalaires -- ceux-ci s'appliquent à tous les composants en parallèle. -
la preuve est simple une fois que vous sachez que c'est le résultat. Si vous demandez quelle est la probabilité que z < Z < z + d z , c'est la même chose que de demander quelle est la probabilité que z < F -1 ( U ) < z + d z appliquer F à tous les trois les expressions de noter que c'est une fonction monotone croissante, d'où F ( z ) < U < F ( z + d z ), développez le côté droit de la trouver F ( z ) + f ( z ) d z , et comme U est uniforme cette probabilité est juste f ( z ) d z comme promis.
-
Cette réponse est basée sur la même "théorie" qui est indiqué par cette réponse
j'ajoute cette réponse comme:
-- Aucune des autres options d'ajustement de l'uniformité "besoin" spot-on " (ou évidemment pas clairement). (Noter pour obtenir la planète comme distribution comportement looking en particulier voulu dans l'ask original, vous venez de rejeter de la liste finie du K uniformément créé points au hasard (au hasard wrt le nombre d'indices dans les K items retour).)
--L'autre impl le plus proche vous a forcé à décider le 'N' par 'l'axe angulaire', vs. juste 'une valeur de N' à travers les deux valeurs de l'axe angulaire ( qui, à de faibles nombres de N est très difficile de savoir ce qui peut, ou peut ne pas avoir d'importance (par exemple, vous voulez '5' points - amusez-vous)
--En outre, il est très difficile de "grok" comment différencier entre les autres options sans aucune imagerie, donc voici à quoi ressemble cette option (ci-dessous), et l'implémentation prête à l'emploi qui va avec.
avec 20:
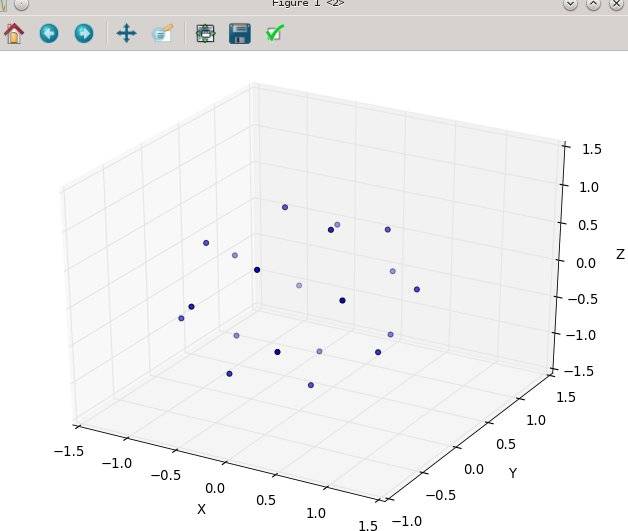
et puis N à 80:
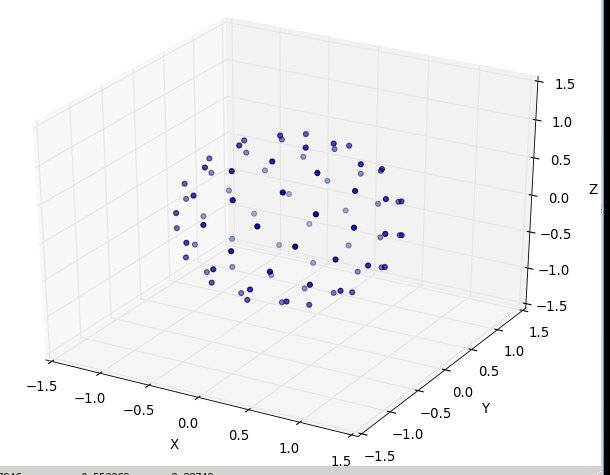
voici le code python3 prêt à l'emploi, où l'émulation est la même source: " http://web.archive.org/web/20120421191837/http://www.cgafaq.info/wiki/Evenly_distributed_points_on_sphere " trouvé par d'autres. ( Le tracé que j'ai inclus, que les incendies quand fonctionnent comme ' principal,' est pris de: http://www.scipy.org/Cookbook/Matplotlib/mplot3D )
from math import cos, sin, pi, sqrt
def GetPointsEquiAngularlyDistancedOnSphere(numberOfPoints=45):
""" each point you get will be of form 'x, y, z'; in cartesian coordinates
eg. the 'l2 distance' from the origion [0., 0., 0.] for each point will be 1.0
------------
converted from: http://web.archive.org/web/20120421191837/http://www.cgafaq.info/wiki/Evenly_distributed_points_on_sphere )
"""
dlong = pi*(3.0-sqrt(5.0)) # ~2.39996323
dz = 2.0/numberOfPoints
long = 0.0
z = 1.0 - dz/2.0
ptsOnSphere =[]
for k in range( 0, numberOfPoints):
r = sqrt(1.0-z*z)
ptNew = (cos(long)*r, sin(long)*r, z)
ptsOnSphere.append( ptNew )
z = z - dz
long = long + dlong
return ptsOnSphere
if __name__ == '__main__':
ptsOnSphere = GetPointsEquiAngularlyDistancedOnSphere( 80)
#toggle True/False to print them
if( True ):
for pt in ptsOnSphere: print( pt)
#toggle True/False to plot them
if(True):
from numpy import *
import pylab as p
import mpl_toolkits.mplot3d.axes3d as p3
fig=p.figure()
ax = p3.Axes3D(fig)
x_s=[];y_s=[]; z_s=[]
for pt in ptsOnSphere:
x_s.append( pt[0]); y_s.append( pt[1]); z_s.append( pt[2])
ax.scatter3D( array( x_s), array( y_s), array( z_s) )
ax.set_xlabel('X'); ax.set_ylabel('Y'); ax.set_zlabel('Z')
p.show()
#end
testé à faible nombre (N en 2, 5, 7, 13, etc) et semble fonctionner "nice "
Ce que vous cherchez est appelé un sphérique . Le problème de couverture sphérique est très difficile et les solutions sont inconnues, sauf pour un petit nombre de points. Une chose qui est sûre est que donné n points sur une sphère, il existe toujours deux points de distance d = (4-csc^2(\pi n/6(n-2)))^(1/2) ou plus proche.
Si vous voulez une méthode probabiliste pour générer des points uniformément répartis sur une sphère, c'est simple: générer des points dans l'espace uniformément par distribution gaussienne (il est construit en Java, pas difficile de trouver le code pour les autres langues). Donc dans l'espace tridimensionnel, vous avez besoin de quelque chose comme
Random r = new Random();
double[] p = { r.nextGaussian(), r.nextGaussian(), r.nextGaussian() };
puis projeter le point sur la sphère en normalisant sa distance de l'origine
double norm = Math.sqrt( (p[0])^2 + (p[1])^2 + (p[2])^2 );
double[] sphereRandomPoint = { p[0]/norm, p[1]/norm, p[2]/norm };
la distribution gaussienne en n dimensions est sphérique symétrique de sorte que la projection sur la sphère est uniforme.
bien sûr, il n'y a aucune garantie que la distance entre deux points dans une collection de points uniformément générés sera limitée ci-dessous, de sorte que vous pouvez utiliser le rejet pour appliquer de telles conditions que vous pourriez avoir: probablement, il est préférable de générer l'ensemble de la collection et puis rejeter l'ensemble de la collection si nécessaire. (Ou utilisez "early rejection" pour rejeter toute la collection que vous avez généré jusqu'à présent; il suffit de ne pas garder certains points et en laisser tomber d'autres.) Vous pouvez utiliser la formule pour d donnée ci-dessus, moins un certain mou, à déterminez la distance minimale entre les points au-dessous de laquelle vous rejetterez un ensemble de points. Vous aurez à calculer n choisir 2 distances, et la probabilité de rejet dépendra du mou; il est difficile de dire comment, alors exécuter une simulation pour obtenir une idée des statistiques pertinentes.
, Essayez:
function sphere ( N:float,k:int):Vector3 {
var inc = Mathf.PI * (3 - Mathf.Sqrt(5));
var off = 2 / N;
var y = k * off - 1 + (off / 2);
var r = Mathf.Sqrt(1 - y*y);
var phi = k * inc;
return Vector3((Mathf.Cos(phi)*r), y, Mathf.Sin(phi)*r);
};
la fonction ci-dessus doit être exécutée en boucle avec une itération totale de la boucle N et une itération du courant de la boucle K.
il est basé sur un motif de graines de tournesol, sauf que les graines de tournesol sont courbées autour dans un demi-dôme, et à nouveau dans une sphère.
Voici une image, sauf que j'ai mis la caméra à mi-chemin à l'intérieur de la sphère pour qu'elle soit 2d au lieu de 3d parce que la caméra est à la même distance de tous les points. http://3.bp.blogspot.com/-9lbPHLccQHA/USXf88_bvVI/AAAAAAAAADY/j7qhQsSZsA8/s640/sphere.jpg
avec un petit nombre de points vous pourriez exécuter une simulation:
from random import random,randint
r = 10
n = 20
best_closest_d = 0
best_points = []
points = [(r,0,0) for i in range(n)]
for simulation in range(10000):
x = random()*r
y = random()*r
z = r-(x**2+y**2)**0.5
if randint(0,1):
x = -x
if randint(0,1):
y = -y
if randint(0,1):
z = -z
closest_dist = (2*r)**2
closest_index = None
for i in range(n):
for j in range(n):
if i==j:
continue
p1,p2 = points[i],points[j]
x1,y1,z1 = p1
x2,y2,z2 = p2
d = (x1-x2)**2+(y1-y2)**2+(z1-z2)**2
if d < closest_dist:
closest_dist = d
closest_index = i
if simulation % 100 == 0:
print simulation,closest_dist
if closest_dist > best_closest_d:
best_closest_d = closest_dist
best_points = points[:]
points[closest_index]=(x,y,z)
print best_points
>>> best_points
[(9.921692138442777, -9.930808529773849, 4.037839326088124),
(5.141893371460546, 1.7274947332807744, -4.575674650522637),
(-4.917695758662436, -1.090127967097737, -4.9629263893193745),
(3.6164803265540666, 7.004158551438312, -2.1172868271109184),
(-9.550655088997003, -9.580386054762917, 3.5277052594769422),
(-0.062238110294250415, 6.803105171979587, 3.1966101417463655),
(-9.600996012203195, 9.488067284474834, -3.498242301168819),
(-8.601522086624803, 4.519484132245867, -0.2834204048792728),
(-1.1198210500791472, -2.2916581379035694, 7.44937337008726),
(7.981831370440529, 8.539378431788634, 1.6889099589074377),
(0.513546008372332, -2.974333486904779, -6.981657873262494),
(-4.13615438946178, -6.707488383678717, 2.1197605651446807),
(2.2859494919024326, -8.14336582650039, 1.5418694699275672),
(-7.241410895247996, 9.907335206038226, 2.271647103735541),
(-9.433349952523232, -7.999106443463781, -2.3682575660694347),
(3.704772125650199, 1.0526567864085812, 6.148581714099761),
(-3.5710511242327048, 5.512552040316693, -3.4318468250897647),
(-7.483466337225052, -1.506434920354559, 2.36641535124918),
(7.73363824231576, -8.460241422163824, -1.4623228616326003),
(10, 0, 0)]
prenez les deux facteurs les plus importants de votre N , si N==20 puis les deux facteurs les plus importants sont {5,4} , ou, plus généralement {a,b} . Calculer
dlat = 180/(a+1)
dlong = 360/(b+1})
mettez votre premier point à {90-dlat/2,(dlong/2)-180} , votre deuxième à {90-dlat/2,(3*dlong/2)-180} , votre troisième à {90-dlat/2,(5*dlong/2)-180} , jusqu'à ce que vous avez trébuché autour du monde une fois, à ce moment-là vous avez à environ {75,150} quand vous allez à côté de {90-3*dlat/2,(dlong/2)-180} .
évidemment, je travaille ceci en degrés à la surface de la Terre sphérique, avec les conventions habituelles pour traduire + / - en N / S ou E / W. et évidemment ceci vous donne une distribution complètement non-aléatoire, mais c'est uniforme et les points ne sont pas groupés ensemble.
pour ajouter un certain degré d'aléatoire, vous pourriez générer 2 normalement distribués (avec moyenne 0 et dév de {dlat/3, dlong/3} selon le cas) et les ajouter à vos points uniformément distribués.
edit: Cela ne répond pas à la question de l'OP voulais dire, la laissant ici dans le cas de gens trouvent qu'il est utile en quelque sorte.
nous utilisons la règle de multiplication de la probabilité, combinée avec des infinitésimales. Il en résulte 2 lignes de code pour atteindre le résultat souhaité:
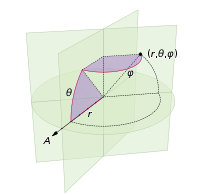
longitude: φ = uniform([0,2pi))
azimuth: θ = -arcsin(1 - 2*uniform([0,1]))
(défini dans le système de coordonnées suivant:)
votre langue a typiquement un nombre aléatoire uniforme primitif. Par exemple en python vous pouvez utiliser random.random() pour retourner un nombre dans la gamme [0,1) . Vous pouvez multiplier ce nombre par k pour obtenir un nombre aléatoire dans la plage [0,k) . Ainsi, en python, uniform([0,2pi)) signifierait random.random()*2*math.pi .
preuve
maintenant, nous ne pouvons pas attribuer θ de façon uniforme, sinon nous nous regrouperions pôle. Nous voulons attribuer des probabilités proportionnelles à la surface du coin sphérique (Le θ dans ce diagramme est en fait φ):
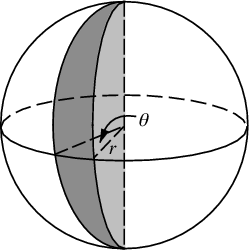
un déplacement angulaire dφ à l'Équateur résultera en un déplacement de dφ*r. Quel sera ce déplacement à un azimut arbitraire θ? Le rayon de l'axe z est r*sin(θ) , donc la longueur de l'Arc de cette" latitude "croisant le coin est dφ * r*sin(θ) . Ainsi nous calculons la distribution cumulative de la zone à échantillonner à partir de celle-ci, en intégrant la zone de la tranche du pôle Sud au pôle Nord.
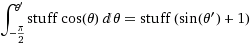(où stuff= dφ*r )
nous allons maintenant essayer d'obtenir l'inverse de la CDF à l'échantillon de celui-ci: http://en.wikipedia.org/wiki/Inverse_transform_sampling
d'abord nous normalisons par diviser notre presque CDF par sa valeur maximale. Cela a pour effet secondaire d'annuler les dφ et R.
azimuthalCDF: cumProb = (sin(θ)+1)/2 from -pi/2 to pi/2
inverseCDF: θ = -sin^(-1)(1 - 2*cumProb)
ainsi:
let x by a random float in range [0,1]
θ = -arcsin(1-2*x)
OR... pour placer 20 points, calculer les centres des faces icosahedronales. Pour 12 points, trouvez les sommets de l'icosaèdre. Pour 30 points, le point milieu des bords de l'icosaèdre. vous pouvez faire la même chose avec le tétraèdre, le cube, le dodécaèdre et les octaèdres: un ensemble de points est sur les sommets, un autre sur le centre de la face et un autre sur le centre des bords. Ils ne peuvent cependant pas être mélangés.
Healpix résout un problème étroitement lié (pixeliser la sphère avec des pixels de surface égale):
http://healpix.sourceforge.net /
c'est probablement exagéré, mais peut-être après l'avoir regardé vous réaliserez que certaines de ses autres belles propriétés sont intéressantes pour vous. C'est bien plus qu'une simple fonction qui produit un nuage de points.
j'ai atterri ici en essayant de le retrouver; le nom "healpix" ne exactement évoquer des sphères...
# create uniform spiral grid
numOfPoints = varargin[0]
vxyz = zeros((numOfPoints,3),dtype=float)
sq0 = 0.00033333333**2
sq2 = 0.9999998**2
sumsq = 2*sq0 + sq2
vxyz[numOfPoints -1] = array([(sqrt(sq0/sumsq)),
(sqrt(sq0/sumsq)),
(-sqrt(sq2/sumsq))])
vxyz[0] = -vxyz[numOfPoints -1]
phi2 = sqrt(5)*0.5 + 2.5
rootCnt = sqrt(numOfPoints)
prevLongitude = 0
for index in arange(1, (numOfPoints -1), 1, dtype=float):
zInc = (2*index)/(numOfPoints) -1
radius = sqrt(1-zInc**2)
longitude = phi2/(rootCnt*radius)
longitude = longitude + prevLongitude
while (longitude > 2*pi):
longitude = longitude - 2*pi
prevLongitude = longitude
if (longitude > pi):
longitude = longitude - 2*pi
latitude = arccos(zInc) - pi/2
vxyz[index] = array([ (cos(latitude) * cos(longitude)) ,
(cos(latitude) * sin(longitude)),
sin(latitude)])
ça marche et c'est très simple. Autant de points que vous voulez:
private function moveTweets():void {
var newScale:Number=Scale(meshes.length,50,500,6,2);
trace("new scale:"+newScale);
var l:Number=this.meshes.length;
var tweetMeshInstance:TweetMesh;
var destx:Number;
var desty:Number;
var destz:Number;
for (var i:Number=0;i<this.meshes.length;i++){
tweetMeshInstance=meshes[i];
var phi:Number = Math.acos( -1 + ( 2 * i ) / l );
var theta:Number = Math.sqrt( l * Math.PI ) * phi;
tweetMeshInstance.origX = (sphereRadius+5) * Math.cos( theta ) * Math.sin( phi );
tweetMeshInstance.origY= (sphereRadius+5) * Math.sin( theta ) * Math.sin( phi );
tweetMeshInstance.origZ = (sphereRadius+5) * Math.cos( phi );
destx=sphereRadius * Math.cos( theta ) * Math.sin( phi );
desty=sphereRadius * Math.sin( theta ) * Math.sin( phi );
destz=sphereRadius * Math.cos( phi );
tweetMeshInstance.lookAt(new Vector3D());
TweenMax.to(tweetMeshInstance, 1, {scaleX:newScale,scaleY:newScale,x:destx,y:desty,z:destz,onUpdate:onLookAtTween, onUpdateParams:[tweetMeshInstance]});
}
}
private function onLookAtTween(theMesh:TweetMesh):void {
theMesh.lookAt(new Vector3D());
}